library(ggplot2)
library(gridExtra)
g1 <- ggplot(data = data.frame(x = seq(-1, 4, 1)), mapping = aes(x = x)) +
stat_function(fun = function(x) 0.1 * x, geom = "line", n = 10, color = "red") +
geom_hline(yintercept = 0) +
geom_vline(xintercept = 0) +
ylim(c(-1, 1)) +
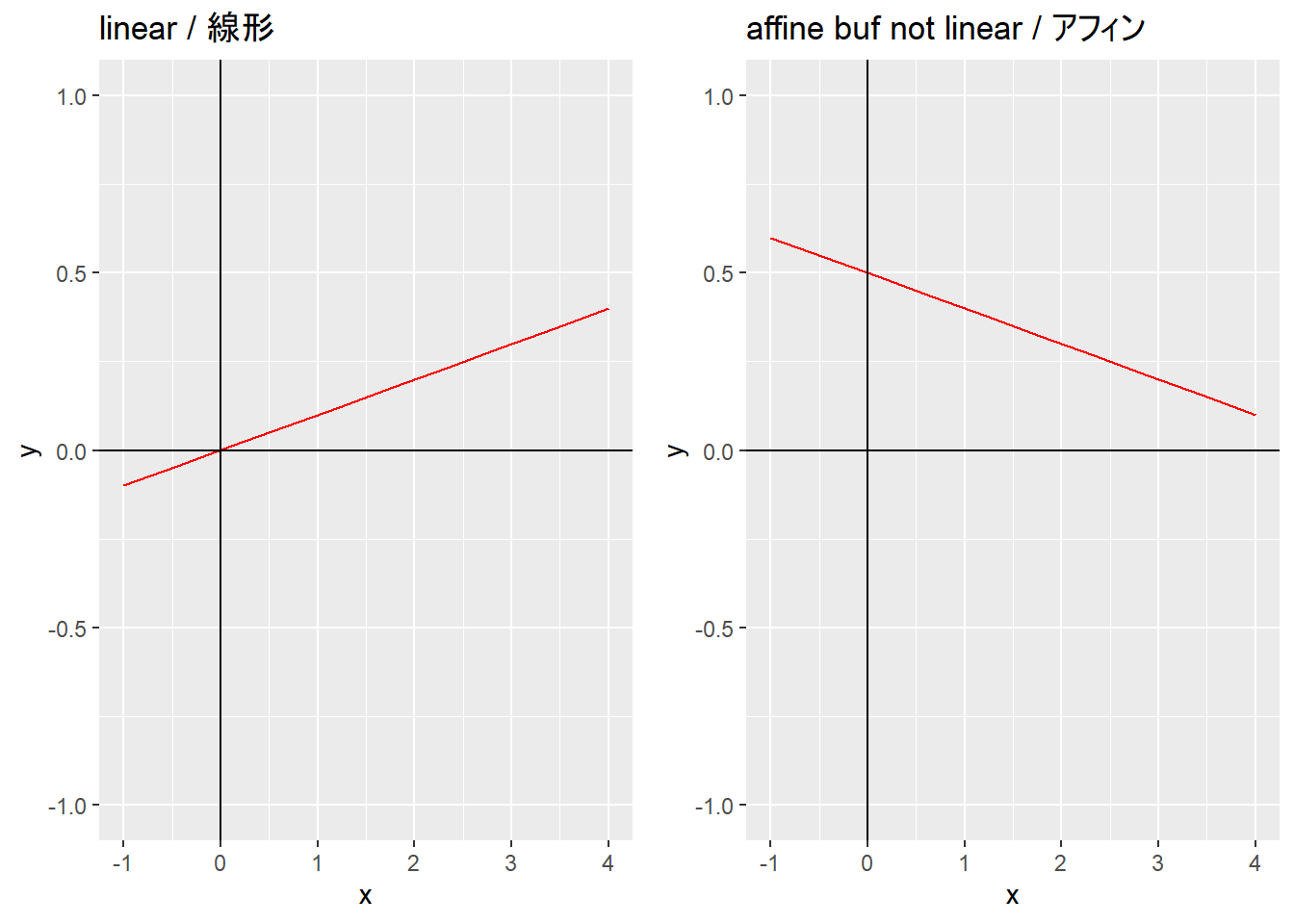
labs(title = "linear / 線形")
g2 <- ggplot(data = data.frame(x = seq(-1, 4, 1)), mapping = aes(x = x)) +
stat_function(fun = function(x) -0.1 * x + 0.5, geom = "line", n = 10, color = "red") +
geom_hline(yintercept = 0) +
geom_vline(xintercept = 0) +
ylim(c(-1, 1)) +
labs(title = "affine buf not linear / アフィン")
ggpubr::as_ggplot(arrangeGrob(g1, g2, ncol = 2))Rで応用線形代数(Reference『Introduction to Applied Linear Algebra Vectors, Matrices, and Least Squares』)
Rでデータサイエンス
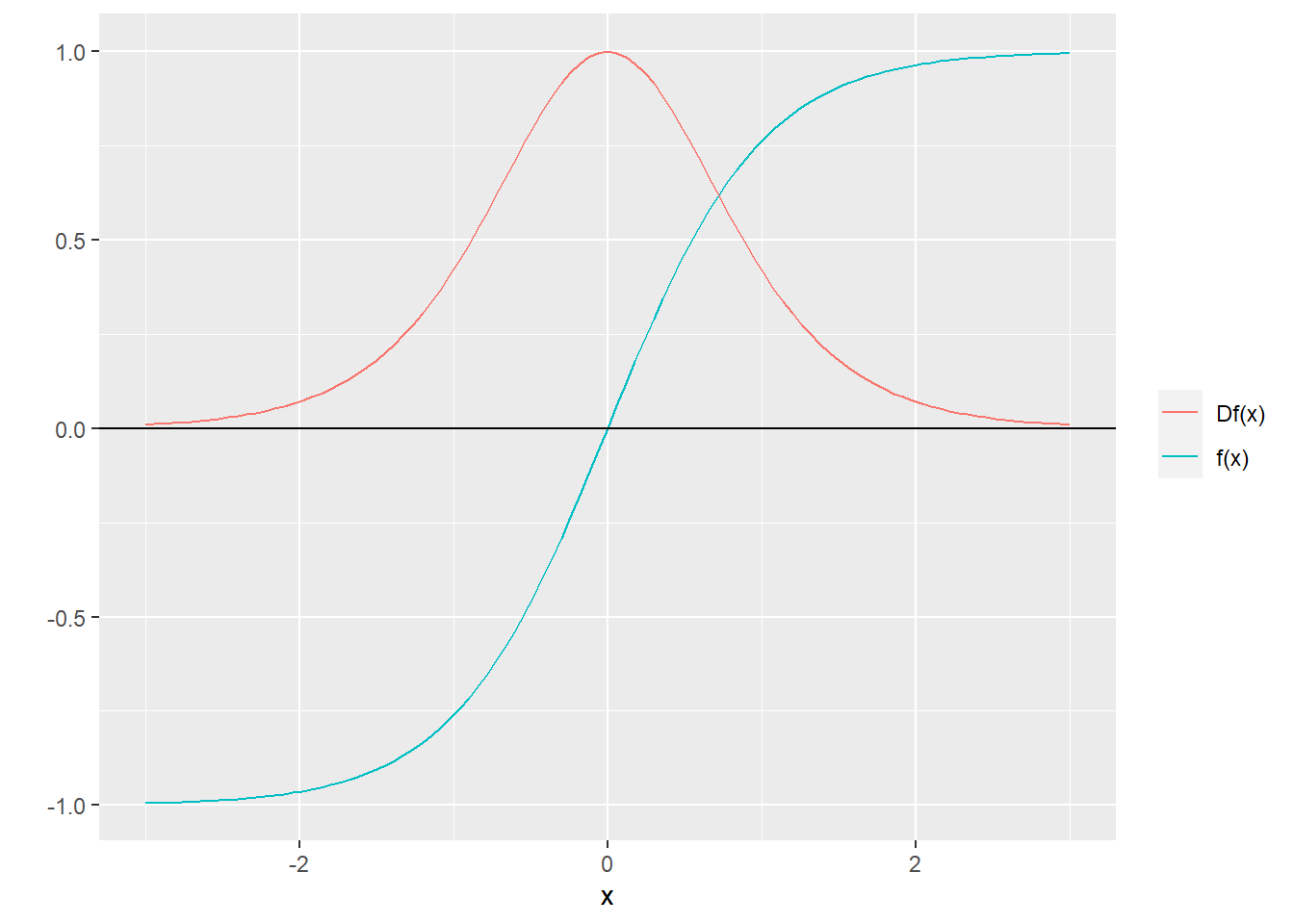
2 Linear functions > 2.1 Linear functions (p.29)
The inner product function. (p.30)
内積の定義は\(\textbf{a},\,\textbf{x}\)を共に\(n\)次元ベクトルとしたときの \[f(\textbf{x})=\textbf{a}^T\textbf{x}=a_1x_1+a_2x_2+\cdots+a_nx_n\] - 関数\(f\)は\(\textbf{x}\)の重み付け和をとる関数と言える。
Superposition and linearity. (p.30)
\(\textbf{x},\textbf{y}\)を\(n\)次元ベクトル、\(\alpha,\beta\)をスカラーとしたとき、内積は以下の性質(線形性、重ね合わせ原理)を満たす。
\[\begin{aligned}f(\alpha\textbf{x}+\beta\textbf{y})=\textbf{a}^T(\alpha\textbf{x}+\beta\textbf{y})=\textbf{a}^T(\alpha\textbf{x})+\textbf{a}^T(\beta\textbf{y})=\alpha(\textbf{a}^T\textbf{x})+\beta(\textbf{a}^T\textbf{y})\end{aligned}=\alpha f(\textbf{x})+\beta f(\textbf{y})\]
また、\(f\)が線形ならば、任意の次元に拡張できる。 \[f(\alpha_1\textbf{x}_1+\cdots+\alpha_k\textbf{x}_k)=\alpha_1f(\textbf{x}_1)+\cdots+\alpha_kf(\textbf{x}_k)\]
さらに、 \[\begin{aligned} f(\alpha_1\textbf{x}_1+\cdots+\alpha_k\textbf{x}_k) &=\alpha_1f(\textbf{x}_1)+f(\alpha_2\textbf{x}_2+ \cdots+\alpha_k\textbf{x}_k)\\ &=\alpha_1f(\textbf{x}_1)+\alpha_2f(\textbf{x}_2)+f(\alpha_3\textbf{x}_3+ \cdots+\alpha_k\textbf{x}_k)\\ &\,\,\,\vdots\\ &=\alpha_1f(\textbf{x}_1)+\cdots+\alpha_kf(\textbf{x}_k) \end{aligned}\]
Inner product representation of a linear function. (p.31)
\(n\)次元ベクトル\(\textbf{x}\)を単位ベクトルを用いて表した上で、
\[f(\textbf{x})=f(x_1e_1+\cdots+x_ne_n)=x_1f(e_1)+\cdots+x_nf(e_n)=\textbf{a}^T\textbf{x}\]
ここで\[\textbf{a}=(f(e_1),f(e_2),\cdots,f(e_n))\]
Affine functions. (p.32)
線形関数に定数項を加えた関数がアフィン関数(アフィン変換、アフィン写像)。
\(f(\textbf{x})=\textbf{a}^T\textbf{x}+b\)かつ\(\alpha+\beta=1\)とするとき、 \[\begin{aligned} f(\alpha\textbf{x}+\beta\textbf{y}) &=\textbf{a}^T(\alpha\textbf{x}+\beta\textbf{y})+b\\ &=\alpha\textbf{a}^T\textbf{x}+\beta\textbf{a}^T\textbf{y}+1\cdot b\\ &=\alpha\textbf{a}^T\textbf{x}+\beta\textbf{a}^T\textbf{y}+(\alpha+\beta)b\\ &=\alpha(\textbf{a}^T\textbf{x}+b)+\beta(\textbf{a}^T\textbf{y}+b)\\ &=\alpha f(\textbf{x})+\beta f(\textbf{y}) \end{aligned}\]
つまり制限を加えた重ね合わせ原理はアフィン関数を意味する。
よって、\(\alpha+\beta=1\)かつ\(f(\alpha\textbf{x}+\beta\textbf{y}\neq\alpha f(\textbf{x})+\beta f(\textbf{y})\)の場合、\(f\)はアフィン関数ではない。
アフィン関数を単位ベクトルを用いて表すと、 \[f(\textbf{x})=f(0)+x_1\left(f(e_1)-f(0)\right)+\cdots+x_n\left(f(e_n)-f(0)\right)\]
ここで\(a_i=f(e_i)-f(0),\quad\,b=f(0)\)
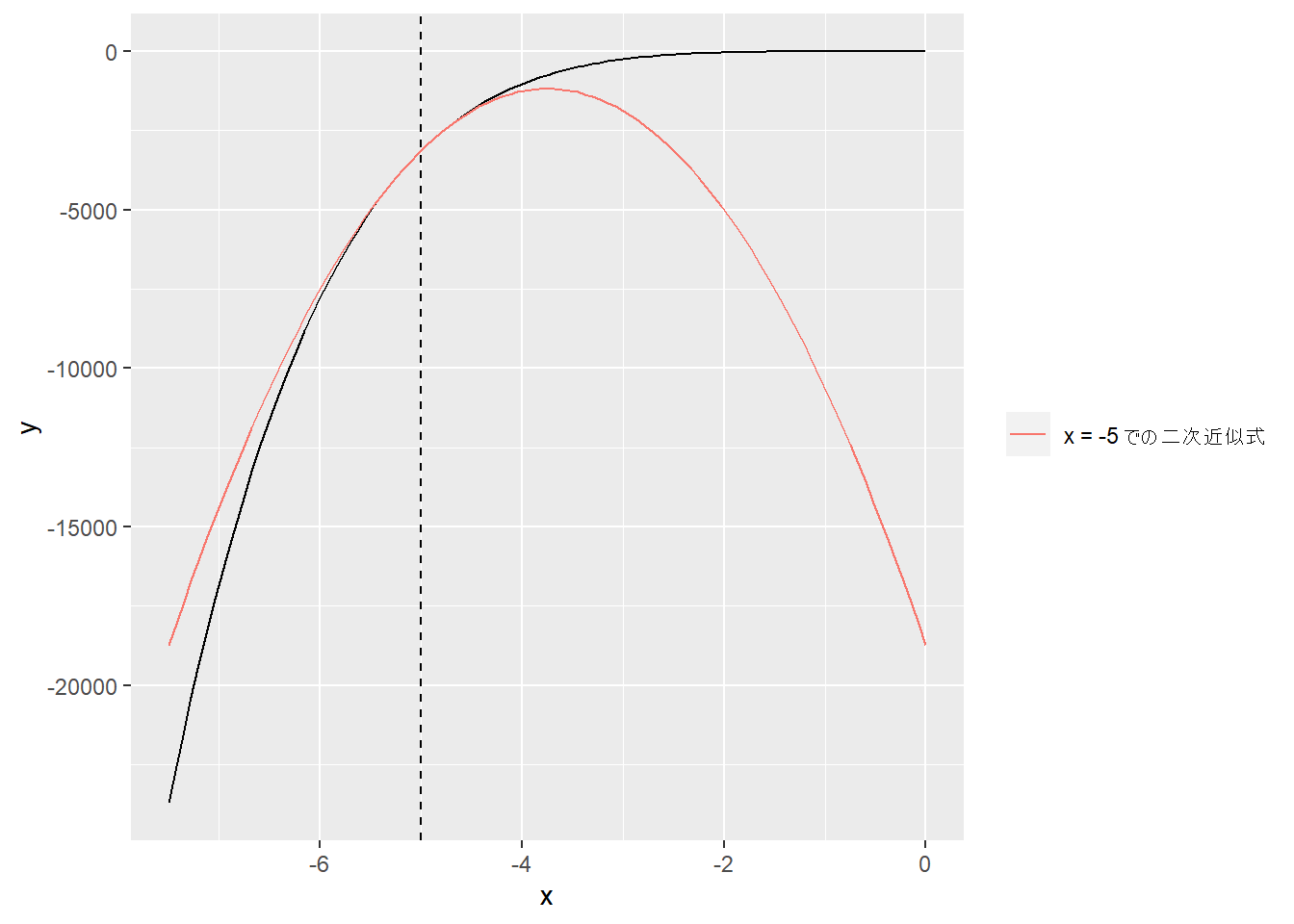
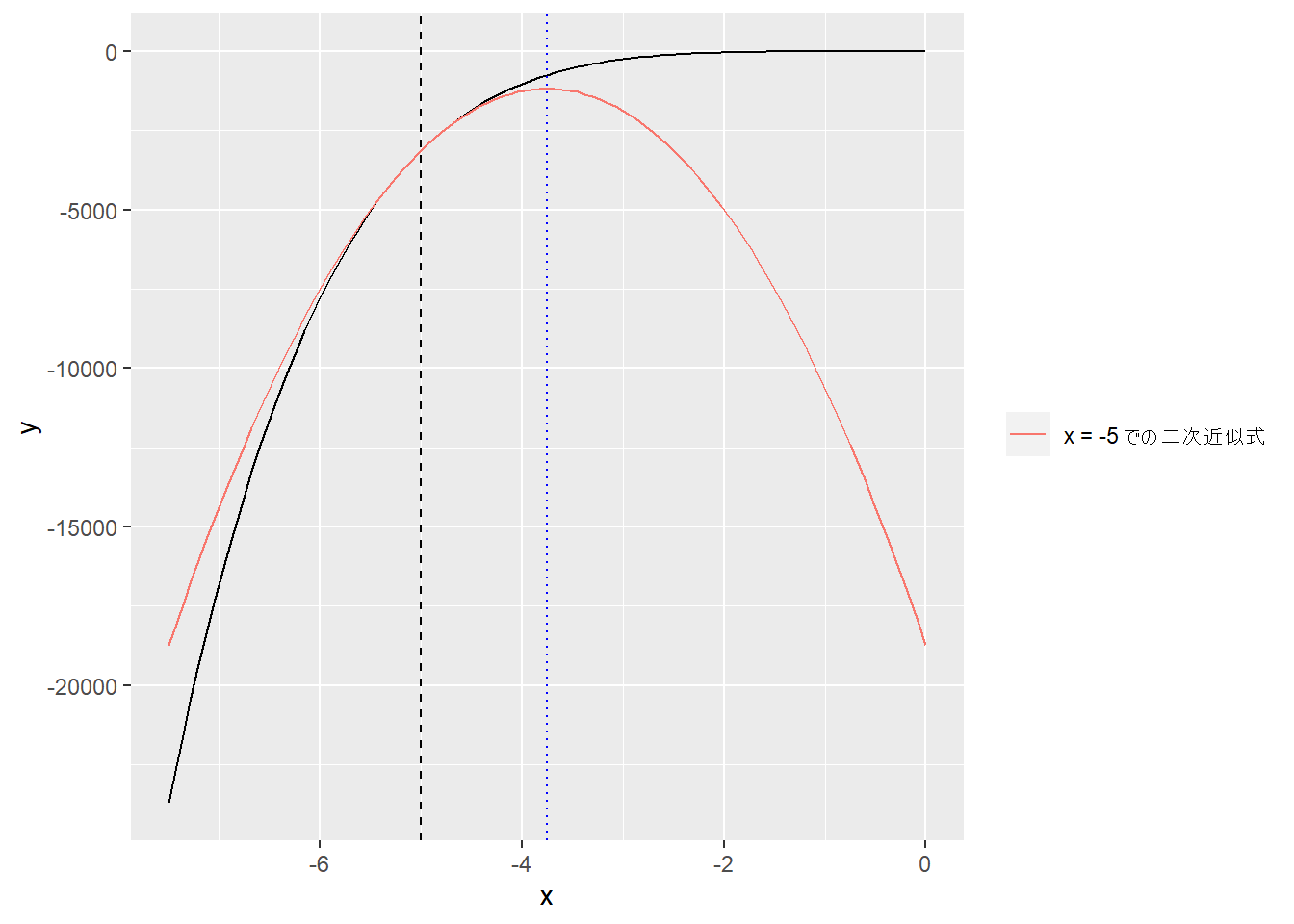
2 Linear functions > 2.2 Taylor approximation (p.35)
アフィンモデルを解くために微分法を利用する。
関数\(f:\textbf{R}^n\rightarrow\textbf{R}\)が微分可能とは、偏微分の存在を意味する。
\(\textbf{z}\)を\(n\)次元ベクトルとしたとき、\(\textbf{z}\)またはその近傍での一次のテイラー展開は
\[\hat{f}(\textbf{x})=f(\textbf{z})+\dfrac{\partial f}{\partial x_1}(\textbf{z})(x_1-z_1)+\cdots+\dfrac{\partial f}{\partial x_n}(\textbf{z})(x_n-z_n)\]
\(\hat{f}\)は\(\textbf{x}\)のアフィン関数であり、\(z\)における\(f\)の勾配を\(n\)次元ベクトル\[\nabla f(z)=\begin{bmatrix}\dfrac{\partial f}{\partial x_1}(z)\\\vdots\\\dfrac{\partial f}{\partial x_n}(z)\end{bmatrix}\]とすると、\[\hat{f}(x)=f(z)+\nabla f(z)^T(x-z)\]と表せられる。
第1項は\(x=z\)のときの定数\(f(z)\)であり、第2項は「\(z\)での\(f\)の勾配」と「\(x\)と\(z\)との偏差」の内積である。
一次のテイラー展開は線形関数と定数項との和で表すことができる。
\[\hat{f}(x)=\nabla f(z)^Tx+\left(f(z)-\nabla f(z)^Tz\right)\]
Example. (p.36)
線形でもアフィンでもない\[f(x)=x_1+\textrm{e}^{x_2-x_1}\]を例とする。
勾配は、 \[\nabla f(z)=\begin{bmatrix}1-\textrm{e}^{z_2-z_1}\\\textrm{e}^{z_2-z_1}\end{bmatrix}\]
library(dplyr)
func_1st_taylor <- function(x, z = c(1, 2)) {
f <- function(x) {
{
x[1] + exp(x[2] - x[1])
} %>% return()
}
grad_f <- function(z) {
c(1 - exp(z[2] - z[1]), exp(z[2] - z[1])) %>% return()
}
f_hat <- function(x, z) {
{
f(x = z) + (grad_f(z = z) %*% (x - z))
} %>% return()
}
list(
x = paste0("(", paste0(format(x, nsmall = 2), collapse = ","), ")"),
`f(x)` = f(x) %>% round(4),
`f_hat(x)` = f_hat(x = x, z = z) %>% round(4),
`|f(x)-f_hat(x)|` = abs(f(x = x) - f_hat(x = x, z = z)) %>% round(4)
)
}
x <- list()
x[[1]] <- c(1.00, 2.00)
x[[2]] <- c(0.96, 1.98)
x[[3]] <- c(1.10, 2.11)
x[[4]] <- c(0.85, 2.05)
x[[5]] <- c(1.25, 2.41)
lapply(seq(x), function(i) func_1st_taylor(x = x[[i]])) %>% Reduce(function(x, y) rbind(x, y), .) x f(x) f_hat(x) |f(x)-f_hat(x)|
x "(1.00,2.00)" 3.7183 3.7183 0
y "(0.96,1.98)" 3.7332 3.7326 0.0005
y "(1.10,2.11)" 3.8456 3.8455 0.0001
y "(0.85,2.05)" 4.1701 4.1119 0.0582
y "(1.25,2.41)" 4.4399 4.4032 0.0367 2 Linear functions > 2.3 Regression model (p.38)
House price regression model. (p.39)
\(y\):住宅販売価格、\(x_1\):床面積、\(x_2\):ベッドルーム数
\[\hat{y}=\textbf{x}^T\beta+v=\beta_1\textbf{x}_1+\beta_2\textbf{x}_2+v\]
# サンプルデータ
list(
baths = table(baths), location = table(location), price = summary(price),
beds = table(beds), area = summary(area), condo = table(condo)
)$baths
baths
1 2 3 4 5
166 493 106 8 1
$location
location
1 2 3 4
26 340 338 70
$price
Min. 1st Qu. Median Mean 3rd Qu. Max.
55.42 150.00 208.00 228.77 284.84 699.00
$beds
beds
1 2 3 4 5 6
8 116 380 223 46 1
$area
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.539 1.146 1.419 1.583 1.836 4.303
$condo
condo
0 1
735 39 result <- lm(price ~ area + beds) %>%
summary() %>%
{
.$coefficients[, 1]
}
result(Intercept) area beds
54.40167 148.72507 -18.85336 beta <- result[2:3] %>% round(2)
v <- result[1] %>% round(2)x <- c(0.846, 1) # 床面積:0.846、ベッドルーム数:1
x %*% beta + v # 予測値
which(area == x[1])
which(area == x[1]) %>% beds[.]
price[which(area == x[1])] # 実際の価格 [,1]
[1,] 161.3756
[1] 476
[1] 1
[1] 115x <- c(1.324, 2) # 床面積:1.324、ベッドルーム数:2
x %*% beta + v # 予測値
which(area == x[1])
which(area == x[1]) %>% beds[.]
price[which(area == x[1])] # 実際の価格 [,1]
[1,] 213.6185
[1] 381
[1] 2
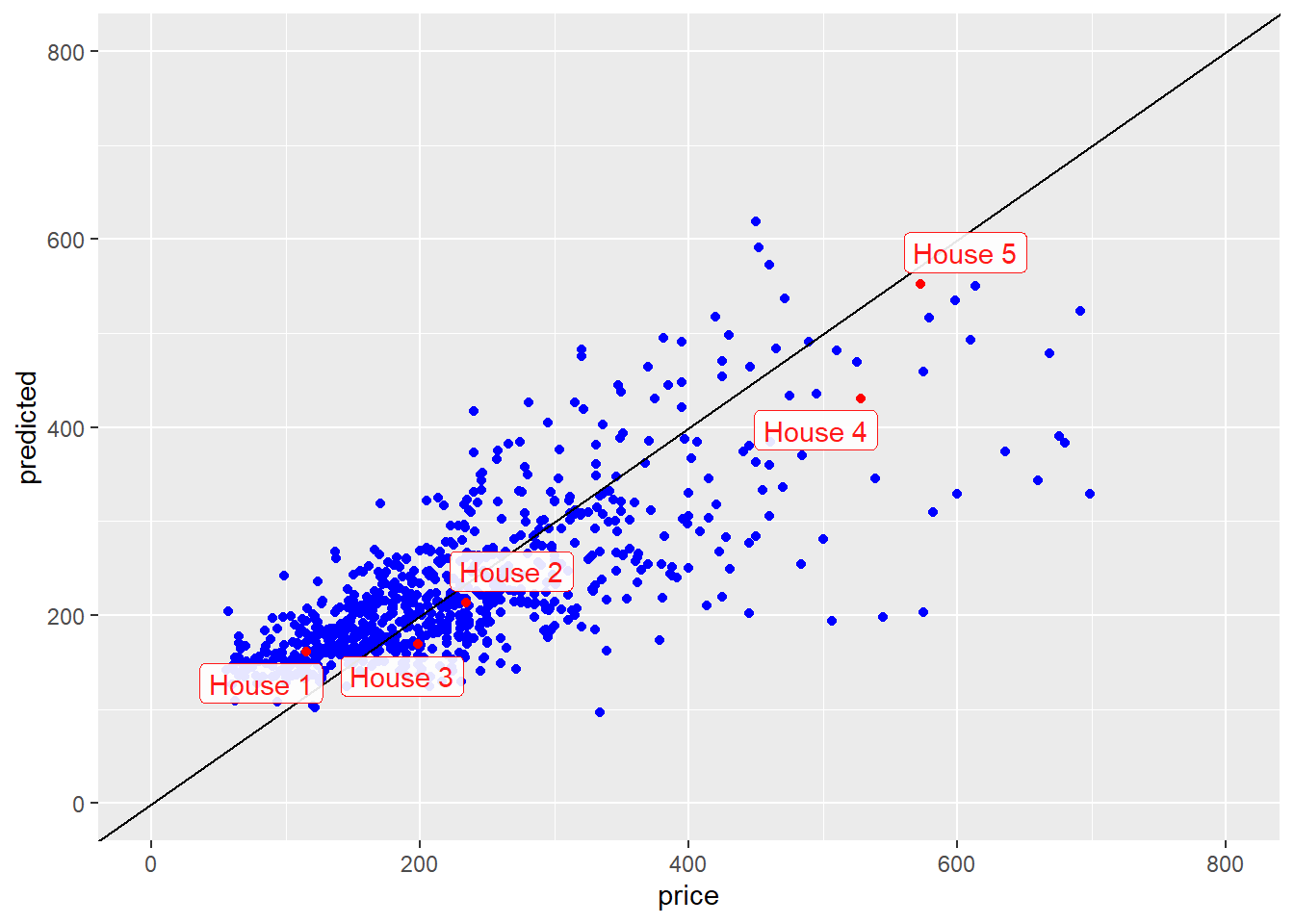
[1] 234.5predicted <- cbind(area, beds) %*% beta + v
df0 <- cbind(
area = c(0.846, 1.324, 1.150, 3.037, 3.984), beds = c(1, 2, 3, 4, 5),
price = c(115.00, 234.50, 198.00, 528.00, 572.50)
)
df <- cbind(df0, predicted = {
df0[, 1:2] %*% beta + v
} %>% as.vector(), obj = paste("House", seq(5))) %>%
data.frame()
ggplot() +
geom_point(mapping = aes(x = price, y = predicted), color = "blue") +
geom_abline(intercept = 0, slope = 1) +
xlim(c(0, 800)) +
ylim(c(0, 800)) +
geom_point(mapping = aes(x = as.numeric(price), y = as.numeric(predicted)), color = "red", data = df) +
geom_label_repel(
mapping = aes(x = as.numeric(price), y = as.numeric(predicted), label = obj),
data = df, alpha = 0.9, color = "red"
)3 Norm and distance > 3.1 Norm (p.45)
\(n\)次元ベクトル\(x\)のユークリッドノルムとは、 \[\|\textbf{x}\|=\displaystyle\sqrt{x_1^2+x_2^2+\cdots+x_n^2}=\displaystyle\sqrt{\textbf{x}^T\textbf{x}}\]
2乗に由来して、\(\|\textbf{x}\|_2\)とも表せられ、「マグニチュード」、「長さ」(ベクトルの次元も長さと呼ばれるため注意)とも呼ばれる。
library(dplyr)
x <- c(2, -1, 2) %>% matrix(ncol = 1)
norm(x = x, type = "2")
x^2 %>%
sum() %>%
sqrt()[1] 3
[1] 3x <- c(0, -1) %>% matrix(ncol = 1)
norm(x = x, type = "2")
x^2 %>%
sum() %>%
sqrt()[1] 1
[1] 1x <- c(3, -1, 2, 4) %>% matrix(ncol = 1)
norm(x = x, type = "1")
x %>%
abs() %>%
sum()[1] 10
[1] 10x <- c(3, -1, 2, 4) %>% matrix(ncol = 1)
norm(x = x, type = "i")
x %>%
abs() %>%
max()[1] 4
[1] 4Root-mean-square value. (p.46)
\[\textrm{rms}(\textbf{x})=\displaystyle\sqrt{\dfrac{x_1^2+\cdots+x_n^2}{n}}=\dfrac{\|\textbf{x}\|}{\sqrt{n}}\]
Norm of a sum. (p.46)
2つのベクトル\(x,y\)の合計のノルム
\[\|\textbf{x}+\textbf{y}\|^2=(\textbf{x}+\textbf{y})^T(\textbf{x}+\textbf{y})=\textbf{x}^T\textbf{x}+\textbf{x}^T\textbf{y}+\textbf{y}^T\textbf{x}+\textbf{y}^T\textbf{y}=\|\textbf{x}\|^2+2\textbf{x}^T\textbf{y}+\|\textbf{y}\|^2\]
よって \[\|\textbf{x}+\textbf{y}\|=\displaystyle\sqrt{\|\textbf{x}\|^2+2\textbf{x}^T\textbf{y}+\|\textbf{y}\|^2}\]
Norm of block vectors. (p.47)
\(\textbf{d}=(\textbf{a},\textbf{b},\textbf{c})\)のノルムは、 \[\|\textbf{d}\|^2=\textbf{d}^T\textbf{d}=\textbf{a}^T\textbf{a}+\textbf{b}^T\textbf{b}+\textbf{c}^T\textbf{c}=\|\textbf{a}\|^2+\|\textbf{b}\|^2+\|\textbf{c}\|^2\]
よって \[\|(\textbf{a},\textbf{b},\textbf{c})\|=\displaystyle\sqrt{\|\textbf{a}\|^2+\|\textbf{b}\|^2+\|\textbf{c}\|^2}=\|(\|\textbf{a}\|,\|\textbf{b}\|,\|\textbf{c}\|)\|\]
3 Norm and distance > 3.2 Distance (p.48)
Euclidean distance. (p.48)
ベクトル\(\textbf{a}\)とベクトル\(\textbf{b}\)のユークリッド距離とは、 \[\textbf{dist}(\textbf{a},\textbf{b})=\|\textbf{a}-\textbf{b}\|\]
library(dplyr)
u <- c(1.8, 2.0, -3.7, 4.7)
v <- c(0.6, 2.1, 1.9, -1.4)
w <- c(2.0, 1.9, -4.0, 4.6)
list(`u-v` = norm(u - v, type = "2"), `u-w` = norm(u - w, type = "2"), `v-w` = norm(v - w, type = "2"))$`u-v`
[1] 8.367795
$`u-w`
[1] 0.3872983
$`v-w`
[1] 8.532878\(u\)と\(v\)では\(u\)の方が\(w\)に近く、\(w\)と\(v\)では\(w\)の方が\(u\)に近い。
Units for heterogeneous vector entries. (p.51)
2つの\(次元n\)ベクトル\(\textbf{x}\)と\(\textbf{y}\)の距離の2乗は、 \[\|\textbf{x}-\textbf{y}\|^2=(x_1-y_1)^2+\cdots+(x_n-y_n)^2\]
# 第1成分は床面積(1000ft^2)、第2成分はベッドルーム数
x <- c(1.6, 2)
y <- c(1.5, 2)
z <- c(1.6, 4)
list(
`x-y` = norm(x - y, type = "2"), `x-z` = norm(x - z, type = "2"), `y-z` = norm(y - z, type = "2"),
`x` = norm(x, type = "2"), `y` = norm(y, type = "2"), `z` = norm(z, type = "2")
)$`x-y`
[1] 0.1
$`x-z`
[1] 2
$`y-z`
[1] 2.002498
$x
[1] 2.56125
$y
[1] 2.5
$z
[1] 4.308132\(\textbf{x}\)と\(\textbf{y}\)が最も近い。
# 第1成分は床面積(ft^2)、第2成分はベッドルーム数
x <- c(1600, 2)
y <- c(1500, 2)
z <- c(1600, 4)
list(
`x-y` = norm(x - y, type = "2"), `x-z` = norm(x - z, type = "2"), `y-z` = norm(y - z, type = "2"),
`x` = norm(x, type = "2"), `y` = norm(y, type = "2"), `z` = norm(z, type = "2")
)$`x-y`
[1] 100
$`x-z`
[1] 2
$`y-z`
[1] 100.02
$x
[1] 1600.001
$y
[1] 1500.001
$z
[1] 1600.005\(\textbf{x}\)と\(\textbf{z}\)が最も近い。つまり単位(unit)の取り方に依存する。
3 Norm and distance > 3.3 Standard deviation (p.52)
\(n\)次元ベクトル\(\textbf{x}\)のStandard deviation(標準偏差)とは、平均除去後の\(\textbf{x}\)のRMSのこと。
\[\textbf{std}(\textbf{x})=\displaystyle\sqrt{\dfrac{(x_1-\textbf{avg}(\textbf{x}))^2+\cdots+(x_n-\textbf{avg}(\textbf{x}))^2}{n}}\]
library(dplyr)
x <- c(1, -2, 3, 2)
# 標本標準偏差
{
sum((x - mean(x))^2) / length(x)
} %>%
{
.^0.5
}[1] 1.870829# 不偏標準偏差
{
sum((x - mean(x))^2) / (length(x) - 1)
} %>%
{
.^0.5
}
sd(x)[1] 2.160247
[1] 2.160247Standardization. (p.56)
標準化したベクトル\(\textbf{x}\)とは
\[\textbf{z}=\dfrac{1}{\textbf{std}(\textbf{x})}(\textbf{x}-\textbf{avg}(\textbf{x})\textbf{1})\]
ここで\(\textbf{1}\)は、全ての要素が1のベクトル(VMLS p.5)。
5 Linear independence > 5.4. Gram-Schmidt algorithm (p.97)
Example. (p.100)
library(dplyr)
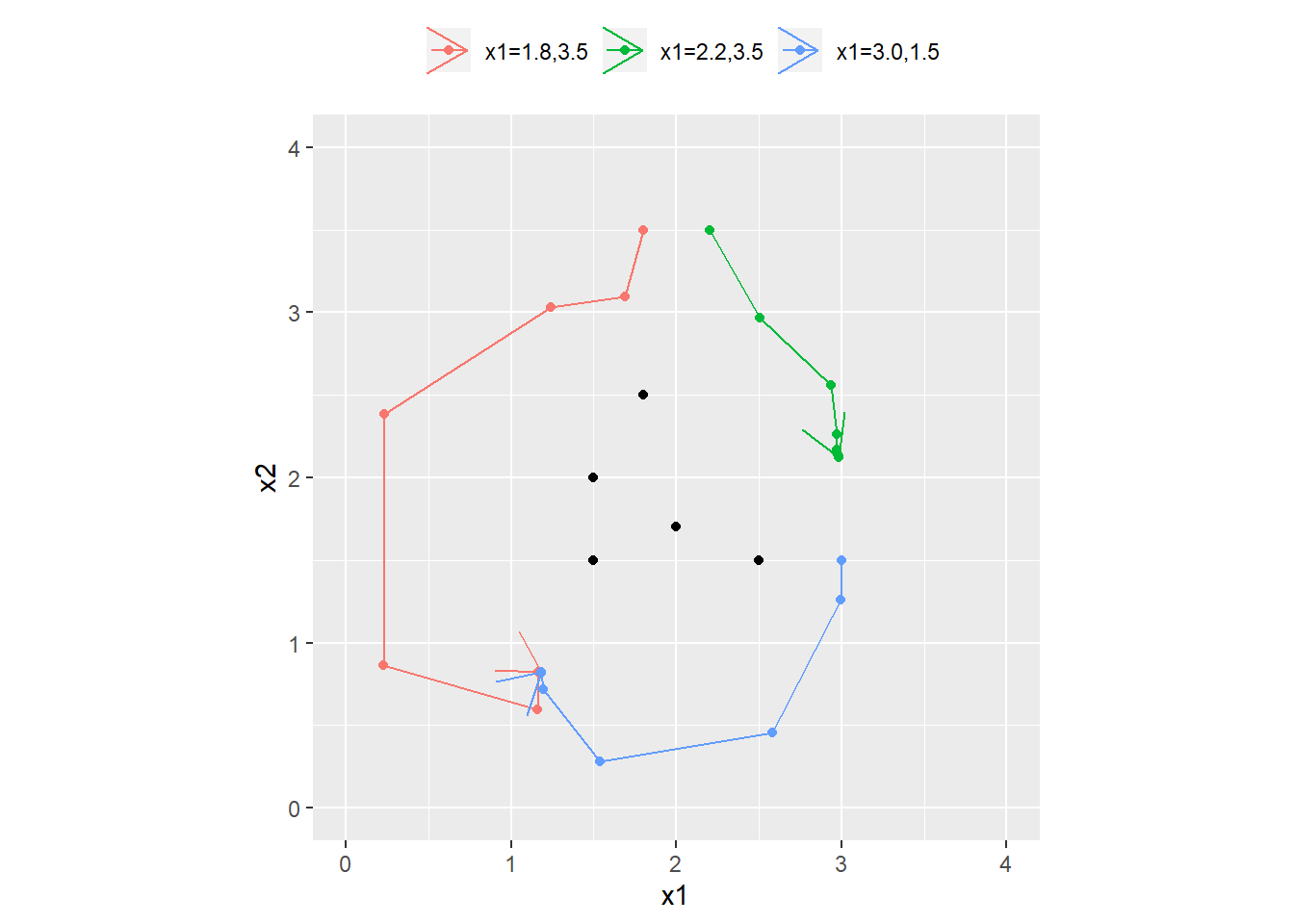
func_Gram_Schmidt_orthonormalization <- function(a, tolerance = 1e-7) {
# Reference https://ses.library.usyd.edu.au/handle/2123/21370
# a: matrix,linearly independent
q <- list()
for (i in seq(nrow(a))) {
q_tilde <- a[i, ]
if (length(q) != 0) {
for (j in seq(length(q))) {
q_tilde <- q_tilde - (q[[j]] %*% a[i, ]) * q[[j]]
}
}
root_sum_square <- q_tilde^2 %>%
sum() %>%
sqrt()
if (root_sum_square < tolerance) {
break
} else {
q_tilde <- q_tilde / root_sum_square
q[[i]] <- q_tilde
}
}
return(list(a = a, q = q, root_sum_square = root_sum_square, i = i))
}# 例1
result <- func_Gram_Schmidt_orthonormalization(a = rbind(c(-1, 1, -1, 1), c(-1, 3, -1, 3), c(1, 3, 5, 7)))
result$a
[,1] [,2] [,3] [,4]
[1,] -1 1 -1 1
[2,] -1 3 -1 3
[3,] 1 3 5 7
$q
$q[[1]]
[1] -0.5 0.5 -0.5 0.5
$q[[2]]
[1] 0.5 0.5 0.5 0.5
$q[[3]]
[1] -0.5 -0.5 0.5 0.5
$root_sum_square
[1] 4
$i
[1] 3q <- result$q
sapply(seq(q), function(x) q[[x]] %>% norm(type = "2"))
combn(seq(q), 2) %>% apply(MARGIN = 2, function(x) q[[x[1]]] %*% q[[x[2]]])[1] 1 1 1
[1] 0 0 0# 例2
result <- func_Gram_Schmidt_orthonormalization(a = sample(0:50, 15, replace = F) %>% matrix(nrow = 5))
result$a
[,1] [,2] [,3]
[1,] 36 33 8
[2,] 38 26 39
[3,] 3 18 24
[4,] 14 9 1
[5,] 31 42 25
$q
$q[[1]]
[1] 0.7274583 0.6668368 0.1616574
$q[[2]]
[1] 0.02175702 -0.25789902 0.96592687
$q[[3]]
[1] -0.6858069 0.6991543 0.2021192
$root_sum_square
[1] 0.000000000000005941509
$i
[1] 4q <- result$q
sapply(seq(q), function(x) q[[x]] %>% norm(type = "2"))
combn(seq(q), 2) %>% apply(MARGIN = 2, function(x) q[[x[1]]] %*% q[[x[2]]])[1] 1 1 1
[1] 0.00000000000000011102230 -0.00000000000000027755576
[3] -0.000000000000000083266736 Matrices > 6.3 Transpose, addition, and norm > 6.3.4 Matrix norm (p.117)
\((m\times n)\)行列\(A\)のノルム(フロベニウスノルム (Frobenius norm) )\(\|\textbf{A}\|\)は、 \[\|\textbf{A}\|=\displaystyle\sqrt{\displaystyle\sum_{i=1}^m\displaystyle\sum_{j=1}^n}A_{ij}^2\]
10 Matrix multiplication > 10.4 QR factorization (p.189)
func_QR_factorization <- function(A) {
# Reference https://ses.library.usyd.edu.au/handle/2123/21370
buf <- func_Gram_Schmidt_orthonormalization(a = t(A))
Q_transpose <- buf$q %>% Reduce(function(x, y) rbind(x, y), .)
R <- Q_transpose %*% A
Q <- Q_transpose %>% t()
QR <- Q %*% R
QQt <- Q %*% t(Q)
return(list(A = A, QR = QR, R = round(R, 10), Q = round(Q, 10), QQt = round(QQt, 10)))
}
n <- 5
A <- rbind(rnorm(n = n) %>% round(2), rnorm(n = n) %>% round(2), rnorm(n = n) %>% round(2))
func_QR_factorization(A = A)$A
[,1] [,2] [,3] [,4] [,5]
[1,] 0.76 0.05 0.79 0.59 1.39
[2,] -1.33 0.12 0.86 -1.06 -0.78
[3,] 0.50 -1.30 0.20 -1.30 0.54
$QR
[,1] [,2] [,3] [,4] [,5]
[1,] 0.76 0.05 0.79 0.59 1.39
[2,] -1.33 0.12 0.86 -1.06 -0.78
[3,] 0.50 -1.30 0.20 -1.30 0.54
$R
[,1] [,2] [,3] [,4] [,5]
x 1.611366 -0.4788484 -0.2751703 0.7497987 1.46695423
y 0.000000 1.2155674 -0.2048960 1.6052914 -0.01945699
y 0.000000 0.0000000 1.1340189 -0.1501386 0.82447966
$Q
x y y
[1,] 0.4716496 0.2269299 0.8520854
[2,] -0.8253867 -0.2264252 0.5171735
[3,] 0.3102958 -0.9472246 0.0805116
$QQt
[,1] [,2] [,3]
[1,] 1 0 0
[2,] 0 1 0
[3,] 0 0 111 Matrix inverses > 11.3 Solving linear equations (p.207)
Back substitution. (p.207)
\(\textbf{R}\)を\((n\times n)\)の上三角行列(対角成分は全て非ゼロ。故に逆行列を持つ)として、\(\textbf{Rx}=\textbf{b}\)を解く。
対角成分より下は全てゼロであるため、 \[\begin{aligned} R_{11}x_1+R_{12}x_2+\cdots+R_{1,n-1}x_{n-1}+R_{1n}x_n&=b_1\\ &\,\,\,\vdots\\ R_{n-2,n-2}x_{n-2}+R_{n-2,n-1}x_{n-1}+R_{n-2,n}x_{n}&=b_{n-2}\\ R_{n-1,n-1}x_{n-1}+R_{n-1,n}x_{n}&=b_{n-1}\\ R_{nn}x_{n}&=b_{n}\\ \end{aligned}\]
最後の行は\(x_{n}=b_{n}/R_{nn}\)となり、\(b_n\)も\(R_{nn}\)も与えられているため\(x_n\)が求められる。求めた\(x_n\)を下から2行目の式に代入すると、
\[x_{n-1}=(b_{n-1}-R_{n-1,n}x_n)/R_{n-1,b-1}\]
求めた\(x_{n-1}\)を下から3行目に代入して、と繰り返すと事によって、\(x_{n-2},x_{n-3},\cdots,x_1\)が求められる(後退代入(back substitution))。
後退代入により\(\textbf{Rx}=\textbf{b},\quad \textbf{x}=\textbf{R}^{-1}\textbf{b}\)が求められる。
library(dplyr)
func_back_substitution <- function(R, b) {
n <- nrow(R)
x <- rep(0, n)
for (i in rev(seq(n))) {
x[i] <- b[i]
j <- i
while (j < n) {
x[i] <- x[i] - R[i, j + 1] * x[j + 1]
j <- j + 1
}
x[i] <- x[i] / R[i, i]
}
return(x)
}
R <- runif(n = 16) %>%
matrix(nrow = 4) %>%
{
.[lower.tri(.)] <- 0
.
}
b <- runif(n = 4)
list(R = R, b = b)$R
[,1] [,2] [,3] [,4]
[1,] 0.6354191 0.377014 0.4446053 0.9687880
[2,] 0.0000000 0.686691 0.8987399 0.2545610
[3,] 0.0000000 0.000000 0.1691899 0.4926958
[4,] 0.0000000 0.000000 0.0000000 0.2151477
$b
[1] 0.5109851 0.5065029 0.6984124 0.2275627x <- func_back_substitution(R = R, b = b)
Rx <-
{
R %*% x
} %>% as.vector()
inv_Rb <-
{
solve(R) %*% b
} %>% as.vector()
cbind(Rx, b, x, inv_Rb) Rx b x inv_Rb
[1,] 0.5109851 0.5109851 -0.9329253 -0.9329253
[2,] 0.5065029 0.5065029 -1.0259244 -1.0259244
[3,] 0.6984124 0.6984124 1.0478511 1.0478511
[4,] 0.2275627 0.2275627 1.0577045 1.057704511 Matrix inverses > 11.4 Examples (p.210)
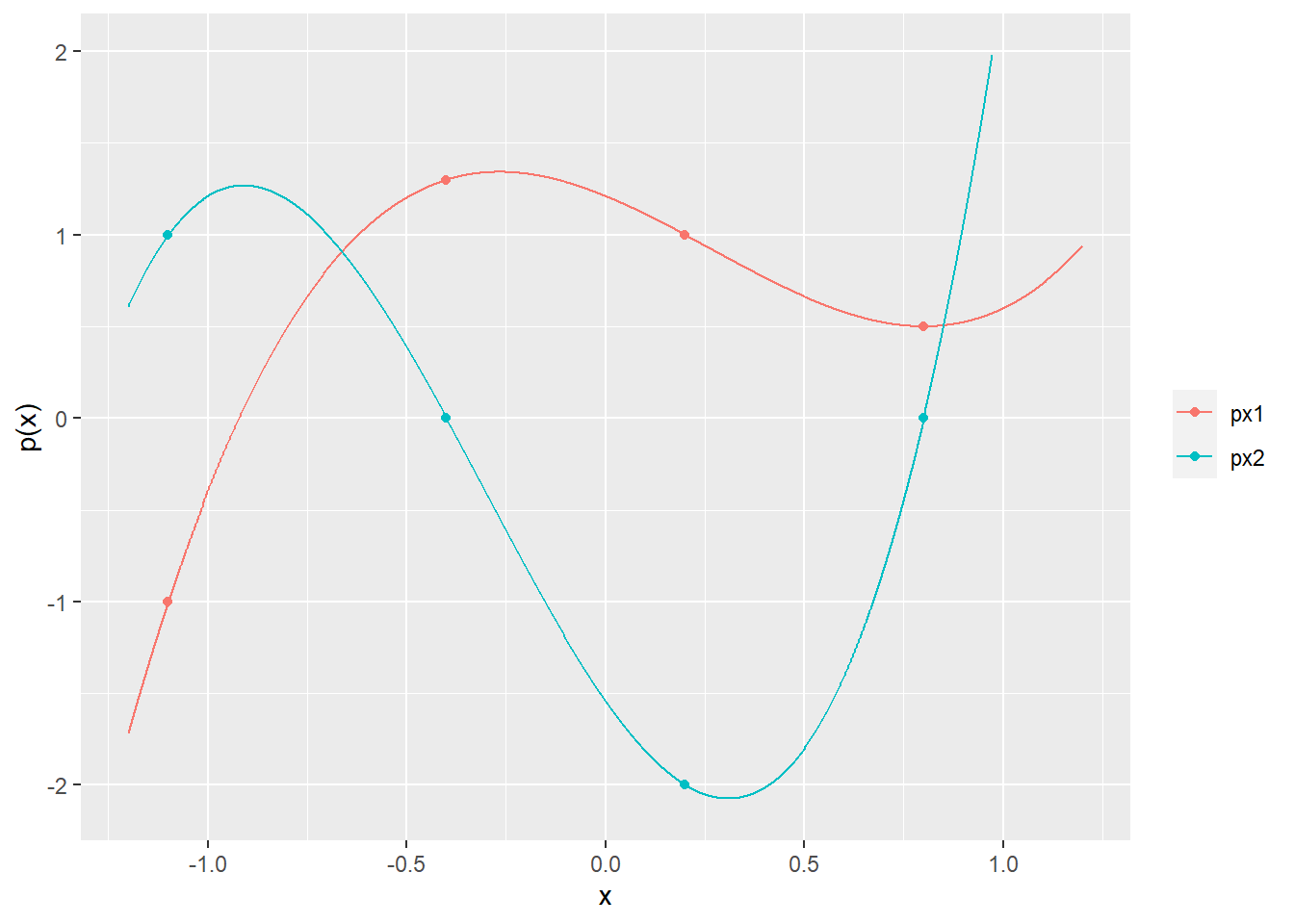
Polynomial interpolation. (p.210)
次の3次多項式について、 \[p(x)=c_1+c_2x+c_3x^2+c_4x^3\]
\[p(-1.1)=b_1,\quad p(-0.4)=b_2,\quad p(0.2)=b_3,\quad p(0.8)=b_4\]を満たす係数\(c\)を求める。
行列表現は\(\textbf{Ac}=\textbf{b}\)となり、\(\textbf{A}\)は \[\textbf{A}=\begin{bmatrix} 1&-1.1&(-1.1)^2&(-1.1)^3\\ 1&-0.4&(-0.4)^2&(-0.4)^3\\ 1&0.2&(0.2)^2&(0.2)^3\\ 1&0.8&(0.8)^2&(0.8)^3 \end{bmatrix}\]となる、ヴァンデルモンド行列。
よって、\(\textbf{c}=\textbf{A}^{-1}\textbf{b}\)を解くと、
library(dplyr)
library(tidyr)
library(ggplot2)
x0 <- c(-1.1, -0.4, 0.2, 0.8)
A <- outer(X = x0, Y = seq(3 + 1) - 1, FUN = "^")
#
b1 <- c(-1.0, 1.3, 1.0, 0.5) # x0のとき、左の点を通過するような c を求める。
c1 <- solve(A) %*% b1
#
b2 <- c(1.0, 0.0, -2.0, 0.0) # x0のとき、左の点を通過するような c を求める。
c2 <- solve(A) %*% b2
#
x <- seq(-1.2, 1.2, length.out = 1000)
A <- outer(X = x, Y = seq(3 + 1) - 1, FUN = "^")
px1 <- A %*% c1
px2 <- A %*% c2
#
tidydf <- data.frame(x, px1, px2) %>% gather(key = "key", value = "value", colnames(.)[-1])
pointdf <- data.frame(x = x0, px1 = b1, px2 = b2) %>% gather(key = "key", value = "value", colnames(.)[-1])
#
ggplot() +
geom_line(data = tidydf, mapping = aes(x = x, y = value, col = key)) +
labs(x = "x", y = "p(x)") +
theme(legend.title = element_blank()) +
geom_point(mapping = aes(x = x, y = value, col = key), data = pointdf) +
ylim(c(-2.1, 2))Balancing chemical reactions. (p.211)
次の化学反応式と解く \[a_1\textrm{Cr}_2\textrm{O}_7^{2-}+a_2\textrm{Fe}^{2+}+a_2\textrm{H}^{+}\rightarrow b_1\textrm{Cr}^{3+}+b_2\textrm{Fe}^{3+}+b_3\textrm{H}_2\textrm{O}\]
library(dplyr)
atoms <- c("Cr", "O", "Fe", "H", "イオン価")
# 反応物(Reactant)
R <- c(2, 7, 0, 0, -2, 0, 0, 1, 0, 2, 0, 0, 0, 1, 1) %>% matrix(ncol = 3)
row.names(R) <- atoms
# 生成物(product)
P <- c(1, 0, 0, 0, 3, 0, 0, 1, 0, 3, 0, 1, 0, 2, 0) %>% matrix(ncol = 3)
row.names(P) <- atoms
list(R = R, P = P)$R
[,1] [,2] [,3]
Cr 2 0 0
O 7 0 0
Fe 0 1 0
H 0 0 1
イオン価 -2 2 1
$P
[,1] [,2] [,3]
Cr 1 0 0
O 0 0 1
Fe 0 1 0
H 0 0 2
イオン価 3 3 0\(a_1=1\)を条件とした場合、
# 係数行列
A <- cbind(R, -1 * P) %>% rbind(., c(1, 0, 0, 0, 0, 0))
# 目的変数
b <- c(0, 0, 0, 0, 0, 1)
#
solve(A) %*% b %>%
{
row.names(.) <- c("a1", "a2", "a3", "b1", "b2", "b3")
t(.)
} a1 a2 a3 b1 b2 b3
[1,] 1 6 14 2 6 711 Matrix inverses > 11.5 Pseudo-inverse (p.214)
Numerical example. (p.216)
非正方行列\(\textbf{A}\)およびベクトル\(\textbf{b}\)を次のとおりとして\(\textbf{Ax}=\textbf{b}\)と解く。
library(dplyr)
A <- c(-3, 4, 1, -4, 6, 1) %>% matrix(ncol = 2)
b <- c(1, -2, 0)列ベクトルが線形独立な行列\(\textbf{A}\)をQR分解
QR <- qr(A)
Q <- qr.Q(QR)
R <- qr.R(QR)
list(Q = Q, R = R)$Q
[,1] [,2]
[1,] -0.5883484 -0.4576043
[2,] 0.7844645 -0.5229764
[3,] 0.1961161 0.7190925
$R
[,1] [,2]
[1,] 5.09902 7.2562970
[2,] 0.00000 -0.5883484擬似逆行列\(\textbf{A}^+\)を求める。
\[\textbf{A}^+=\textbf{R}^{-1}\textbf{Q}^T\]
pseudo_inverse_A <- {
solve(R) %*% t(Q)
}
pseudo_inverse_A [,1] [,2] [,3]
[1,] -1.2222222 -1.1111111 1.777778
[2,] 0.7777778 0.8888889 -1.222222# 擬似逆行列を利用して x を求める。
x <- pseudo_inverse_A %*% b
x [,1]
[1,] 1
[2,] -1# 確認
cbind(Ax = A %*% x %>% round(10) %>% as.vector(), b = b) Ax b
[1,] 1 1
[2,] -2 -2
[3,] 0 012 Least squares > 12.1 Least squares problem (p.225)
\[\textbf{A}=\textbf{xb}\]
library(dplyr)
A <- c(2, 0, -1, 1, 0, 2) %>% matrix(nrow = 3, byrow = T)
b <- c(1, 0, -1) %>% matrix(ncol = 1)
# 優決定系(over-determined)故に解無し。\[\hat{\textbf{x}}=\left(\textbf{A}^{'}\textbf{A}\right)^{-1}\textbf{A}^{'}\textbf{b}=\textbf{A}^{+}\textbf{b}\]ここで、\(\textbf{A}^{+}\)は\(\textbf{A}\)の一般化逆行列
# xの推定量
x_hat <- solve(t(A) %*% A) %*% t(A) %*% b
x_hat [,1]
[1,] 0.3333333
[2,] -0.3333333# 残差
r_hat <- A %*% x_hat - b
r_hat [,1]
[1,] -0.3333333
[2,] -0.6666667
[3,] 0.3333333# 残差のノルムの自乗
norm(r_hat, type = "2")^2[1] 0.666666712 Least squares > 12.4 Examples (p.234)
Advertising purchases. (p.234)
\(\textbf{y}=\textbf{Ax}\)
library(dplyr)
A <- c(
0.97, 1.86, 0.41,
1.23, 2.18, 0.53,
0.80, 1.24, 0.62,
1.29, 0.98, 0.51,
1.10, 1.23, 0.69,
0.67, 0.34, 0.54,
0.87, 0.26, 0.62,
1.10, 0.16, 0.48,
1.92, 0.22, 0.71,
1.29, 0.12, 0.62
) %>% matrix(ncol = 3, byrow = T)
A_ramge <- max(A) / min(A)
y <- rep(10^3, nrow(A)) %>% matrix(ncol = 1)
list(A = A, A_ramge = A_ramge, y = y)$A
[,1] [,2] [,3]
[1,] 0.97 1.86 0.41
[2,] 1.23 2.18 0.53
[3,] 0.80 1.24 0.62
[4,] 1.29 0.98 0.51
[5,] 1.10 1.23 0.69
[6,] 0.67 0.34 0.54
[7,] 0.87 0.26 0.62
[8,] 1.10 0.16 0.48
[9,] 1.92 0.22 0.71
[10,] 1.29 0.12 0.62
$A_ramge
[1] 18.16667
$y
[,1]
[1,] 1000
[2,] 1000
[3,] 1000
[4,] 1000
[5,] 1000
[6,] 1000
[7,] 1000
[8,] 1000
[9,] 1000
[10,] 1000\(\textbf{b}=\textbf{Q}^{'}\textbf{y}\)
QR <- qr(x = A)
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
b <- t(Q) %*% y
list(Q = Q, R = R, b = b)$Q
[,1] [,2] [,3]
[1,] -0.2617400 -0.48336838 0.21255760
[2,] -0.3318971 -0.54118838 0.23326187
[3,] -0.2158680 -0.28051919 -0.44193172
[4,] -0.3480872 -0.04271022 0.23104990
[5,] -0.2968185 -0.19486267 -0.30605721
[6,] -0.1807895 0.04571691 -0.47254161
[7,] -0.2347565 0.13228601 -0.45820183
[8,] -0.2968185 0.23505481 0.04529853
[9,] -0.5180832 0.43409279 0.34276081
[10,] -0.3480872 0.30283093 -0.07258117
$R
[,1] [,2] [,3]
[1,] -3.705968 -2.510005 -1.7686876
[2,] 0.000000 -2.488850 -0.0996784
[3,] 0.000000 0.000000 -0.4757187
$b
[,1]
[1,] -3032.9456
[2,] -392.6674
[3,] -686.3848\(\textbf{Rx}=\textbf{b}\)
x_hat <- solve(a = R) %*% b %>% round()
x_hat [,1]
[1,] 62
[2,] 100
[3,] 1443# RMS error
A %>%
apply(MARGIN = 1, function(x) x %*% x_hat) %>%
{
. - y
} %>%
{
sqrt(sum(.^2) / nrow(A))
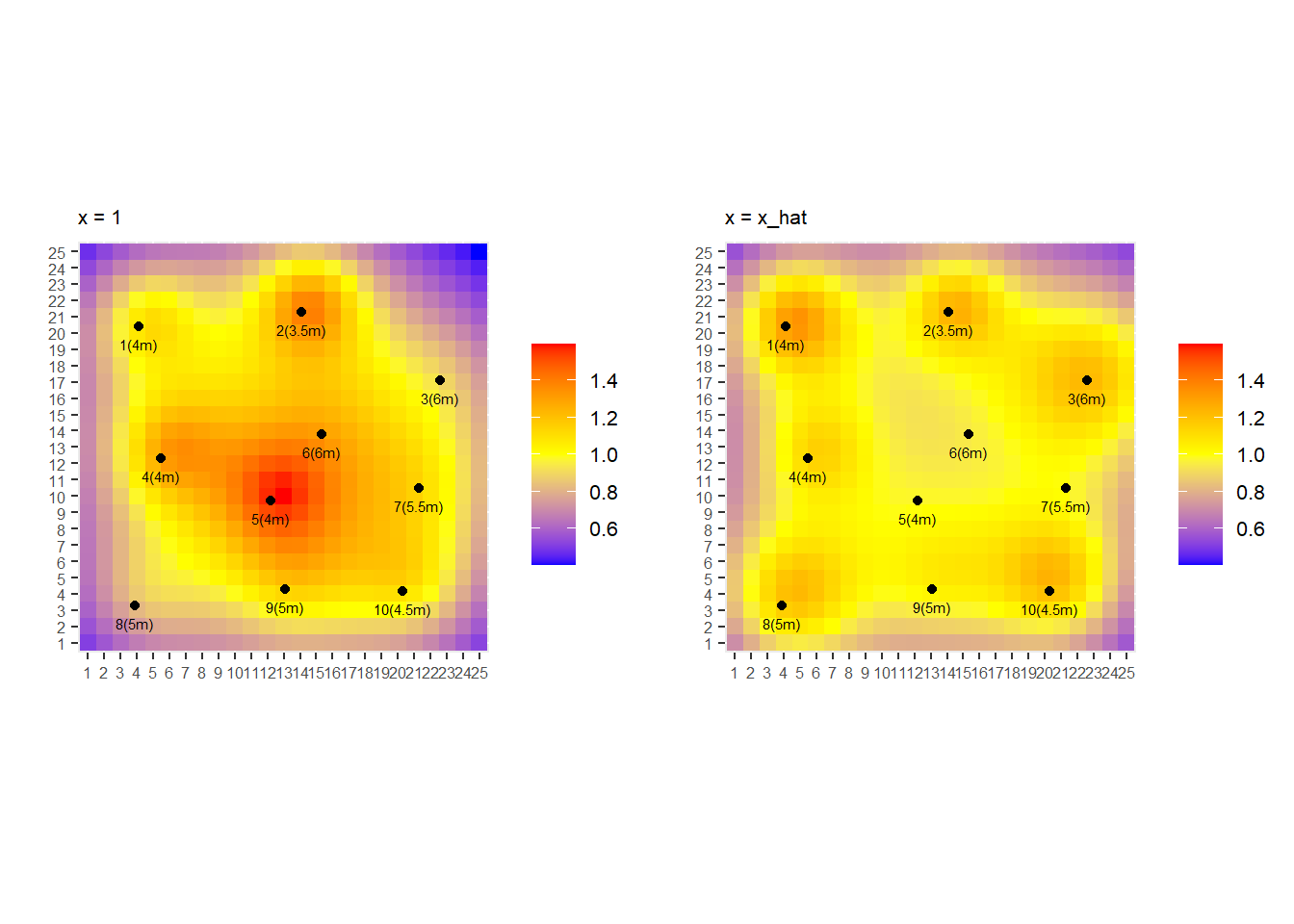
}[1] 132.6382Illumination. (p.234)
# Extracted from 『https://ses.library.usyd.edu.au/handle/2123/21370』
library(ggplot2)
library(reshape2)
library(dplyr)
library(gridExtra)
n <- 10
lamps <- c(
4.1, 20.4, 4.0,
14.1, 21.3, 3.5,
22.6, 17.1, 6.0,
5.5, 12.3, 4.0,
12.2, 9.7, 4.0,
15.3, 13.8, 6.0,
21.3, 10.5, 5.5,
3.9, 3.3, 5.0,
13.1, 4.3, 5.0,
20.3, 4.2, 4.5
) %>% matrix(nrow = n, byrow = T)N <- 25
m <- N^2
tmp <- seq(from = 0.5, by = 1, length.out = N)
pixels <- cbind(tmp %>% sapply(function(x) rep(x, length(tmp))) %>% as.vector(), rep(tmp, length(tmp)), 0)
head(pixels, 3)
tail(pixels, 3) [,1] [,2] [,3]
[1,] 0.5 0.5 0
[2,] 0.5 1.5 0
[3,] 0.5 2.5 0
[,1] [,2] [,3]
[623,] 24.5 22.5 0
[624,] 24.5 23.5 0
[625,] 24.5 24.5 0A <- matrix(data = 0, nrow = m, ncol = n)
for (i in seq(m)) {
for (j in seq(n)) {
A[i, j] <-
{
pixels[i, ] - lamps[j, ]
} %>%
matrix(nrow = 1) %>%
norm(type = "2") %>%
{
.^2
} %>%
{
1 / .
}
}
}
A <- (m / sum(A)) * A
y <- rep(1, m) %>% matrix(ncol = 1)QR <- qr(x = A)
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
b <- t(Q) %*% yx_hat <- solve(a = R) %*% b
x_hat [,1]
[1,] 1.46211018
[2,] 0.78797433
[3,] 2.96641047
[4,] 0.74358042
[5,] 0.08317333
[6,] 0.21263945
[7,] 0.21218408
[8,] 2.05114815
[9,] 0.90760315
[10,] 1.47222464# RMS error
A %>%
apply(MARGIN = 1, function(x) x %*% x_hat) %>%
{
. - y
} %>%
{
sqrt(sum(.^2) / nrow(A))
}[1] 0.1403905gg <- list()
intensity <- A %*% matrix(data = 1, nrow = 10) %>% matrix(nrow = N, byrow = T)
df <- melt(intensity)
df$Var1 <- factor(df$Var1, levels = df$Var1 %>% unique())
df$Var2 <- factor(df$Var2, levels = df$Var2 %>% unique())
valuelimits <- df$value %>% range()
g <- ggplot(df, mapping = aes(x = Var1, y = Var2, fill = value)) +
geom_tile() +
scale_fill_gradient2(
low = "blue", high = "red", mid = "yellow",
midpoint = valuelimits %>% mean(), limits = valuelimits
) +
labs(title = "x = 1", x = "", y = "") +
theme(
legend.title = element_blank(),
axis.text = element_text(size = 6),
legend.text = element_text(size = 8),
plot.title = element_text(size = 8)
) +
coord_fixed()
pointdf <- lamps %>%
data.frame() %>%
{
colnames(.) <- c("Var1", "Var2", "value")
.
}
gg[[1]] <- g + geom_point(data = pointdf, mapping = aes(x = Var1, y = Var2)) +
geom_text(
data = pointdf, mapping = aes(label = paste0(seq(nrow(pointdf)), "(", value, "m)")),
hjust = 0.5, vjust = 2, size = 2
)intensity <- A %*% x_hat %>% matrix(nrow = N, byrow = T)
df <- melt(intensity)
df$Var1 <- factor(df$Var1, levels = df$Var1 %>% unique())
df$Var2 <- factor(df$Var2, levels = df$Var2 %>% unique())
g <- ggplot(df, mapping = aes(x = Var1, y = Var2, fill = value)) +
geom_tile() +
scale_fill_gradient2(
low = "blue", high = "red", mid = "yellow",
midpoint = valuelimits %>% mean(), limits = valuelimits
) +
labs(title = "x = x_hat", x = "", y = "") +
theme(
legend.title = element_blank(),
axis.text = element_text(size = 6),
legend.text = element_text(size = 8),
plot.title = element_text(size = 8)
) +
coord_fixed()
gg[[2]] <- g + geom_point(data = pointdf, mapping = aes(x = Var1, y = Var2)) +
geom_text(
data = pointdf, mapping = aes(label = paste0(seq(nrow(pointdf)), "(", value, "m)")),
hjust = 0.5, vjust = 2, size = 2
)13 Least squares data fitting > 13.1 Least squares data fitting > 13.1.1 Fitting univariate functions (p.249)
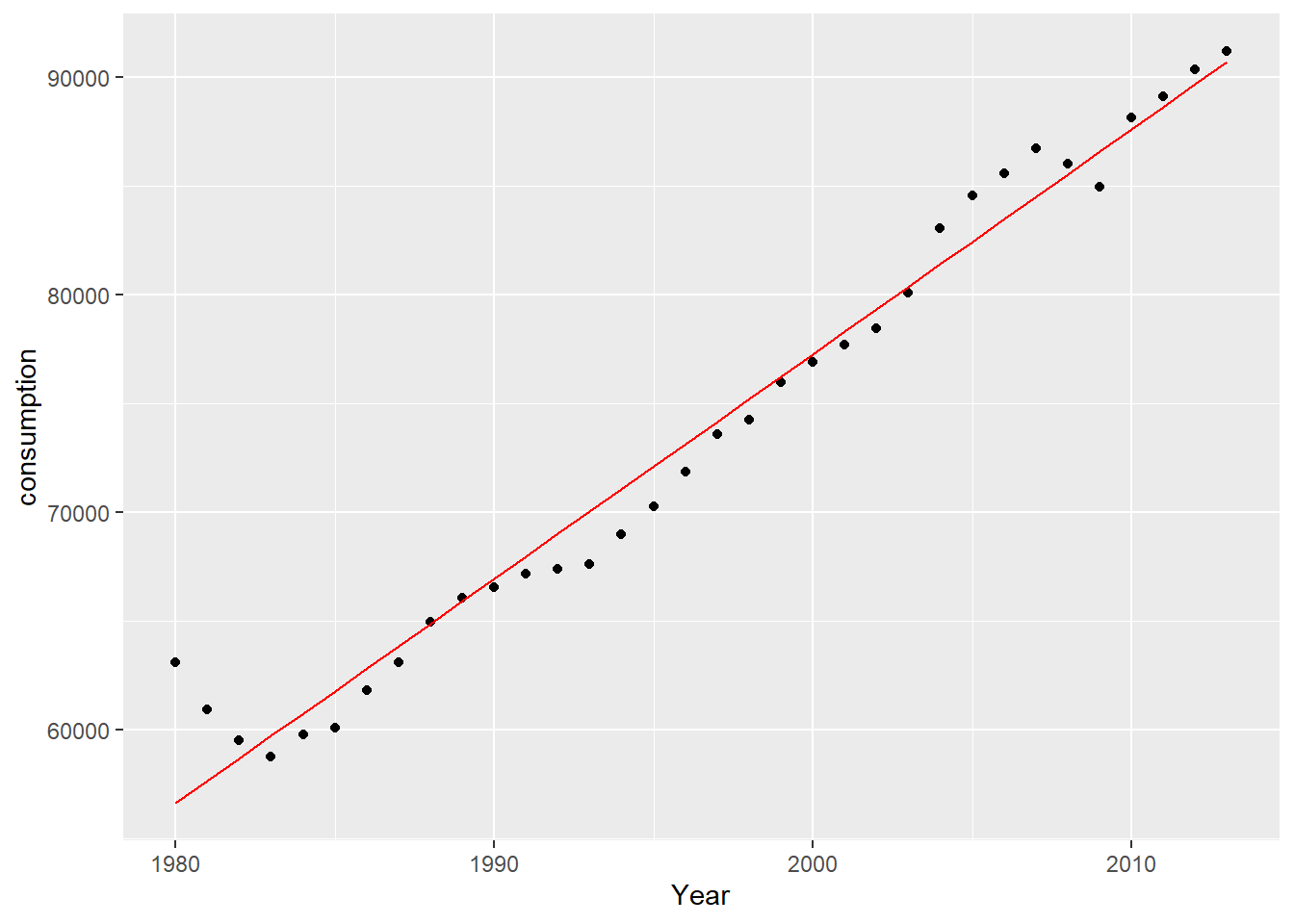
Straight-line fit. (p.249)
consumption <- c(
63122, 60953, 59551, 58785, 59795, 60083, 61819, 63107, 64978, 66090,
66541, 67186, 67396, 67619, 69006, 70258, 71880, 73597, 74274, 75975,
76928, 77732, 78457, 80089, 83063, 84558, 85566, 86724, 86046, 84972,
88157, 89105, 90340, 91195
)
n <- length(consumption)
A <- cbind(rep(1, n), seq(0, n - 1, 1))
QR <- qr(x = A)
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
b <- t(Q) %*% consumption
x_hat <- solve(a = R) %*% b
x_hat
Year <- seq(1980, 2013, 1)
fitting <- cbind(Year, A %*% x_hat)
ggplot() +
geom_point(mapping = aes(x = Year, y = consumption)) +
geom_line(mapping = aes(x = fitting[, 1], y = fitting[, 2]), color = "red") [,1]
[1,] 56637.50
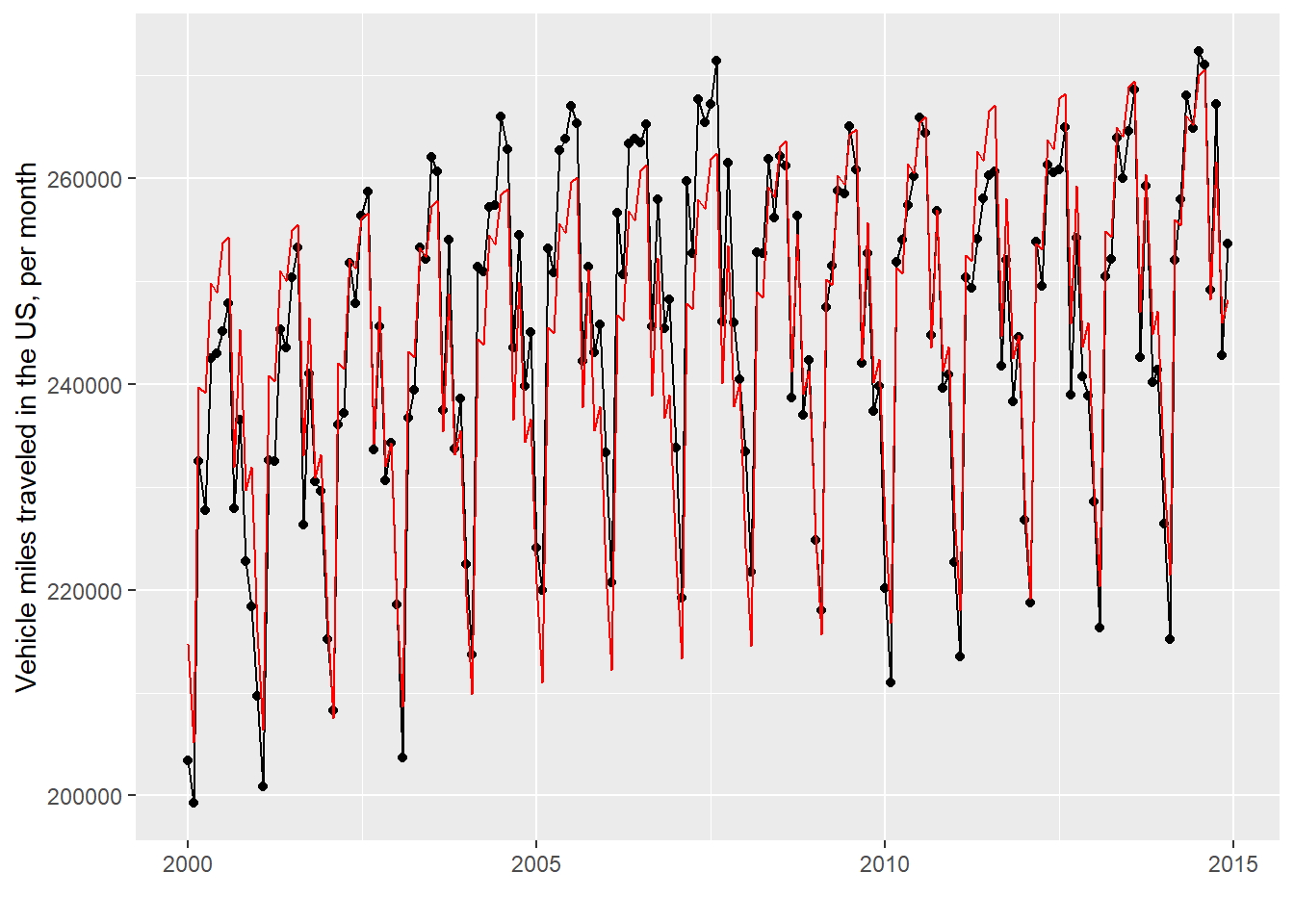
[2,] 1032.57Estimation of trend and seasonal component. (p.252)
vmt <- c(
203442, 199261, 232490, 227698, 242501, 242963, 245140, 247832, 227899, 236491, 222819, 218390, # 2000
209685, 200876, 232587, 232513, 245357, 243498, 250363, 253274, 226312, 241050, 230511, 229584, # 2001
215215, 208237, 236070, 237226, 251746, 247868, 256392, 258666, 233625, 245556, 230648, 234260, # 2002
218534, 203677, 236679, 239415, 253244, 252145, 262105, 260687, 237451, 254048, 233698, 238538, # 2003
222450, 213709, 251403, 250968, 257235, 257383, 265969, 262836, 243515, 254496, 239796, 245029, # 2004
224072, 219970, 253182, 250860, 262678, 263816, 267025, 265323, 242240, 251419, 243056, 245787, # 2005
233302, 220730, 256645, 250665, 263393, 263805, 263442, 265229, 245624, 257961, 245367, 248208, # 2006
233799, 219221, 259740, 252734, 267646, 265475, 267179, 271401, 246050, 261505, 245928, 240444, # 2007
233469, 221728, 252773, 252699, 261890, 256152, 262152, 261228, 238701, 256402, 237009, 242326, # 2008
224840, 218031, 247433, 251481, 258793, 258487, 265026, 260838, 242034, 252683, 237342, 239774, # 2009
220177, 210968, 251858, 254014, 257401, 260159, 265861, 264358, 244712, 256867, 239656, 240932, # 2010
222724, 213547, 250410, 249309, 254145, 258025, 260317, 260623, 241764, 252058, 238278, 244615, # 2011
226834, 218714, 253785, 249567, 261355, 260534, 260880, 264983, 239001, 254170, 240734, 238876, # 2012
228607, 216306, 250496, 252116, 263923, 260023, 264570, 268609, 242582, 259281, 240146, 241365, # 2013
226444, 215166, 252089, 257947, 268075, 264868, 272335, 271018, 249125, 267185, 242816, 253618 # 2014
) %>% matrix(nrow = 15, ncol = 12, byrow = T)
head(vmt)
# 15年12ヶ月。計180ヶ月分 [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 203442 199261 232490 227698 242501 242963 245140 247832 227899 236491
[2,] 209685 200876 232587 232513 245357 243498 250363 253274 226312 241050
[3,] 215215 208237 236070 237226 251746 247868 256392 258666 233625 245556
[4,] 218534 203677 236679 239415 253244 252145 262105 260687 237451 254048
[5,] 222450 213709 251403 250968 257235 257383 265969 262836 243515 254496
[6,] 224072 219970 253182 250860 262678 263816 267025 265323 242240 251419
[,11] [,12]
[1,] 222819 218390
[2,] 230511 229584
[3,] 230648 234260
[4,] 233698 238538
[5,] 239796 245029
[6,] 243056 245787m <- 15 * 12
A <- lapply(seq(15), function(x) diag(x = 1, nrow = 12)) %>%
Reduce(function(x, y) rbind(x, y), .) %>%
cbind(seq(m) - 1, .)
list(head_A = head(A), tail_A = tail(A), dim_A = dim(A))$head_A
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
[1,] 0 1 0 0 0 0 0 0 0 0 0 0 0
[2,] 1 0 1 0 0 0 0 0 0 0 0 0 0
[3,] 2 0 0 1 0 0 0 0 0 0 0 0 0
[4,] 3 0 0 0 1 0 0 0 0 0 0 0 0
[5,] 4 0 0 0 0 1 0 0 0 0 0 0 0
[6,] 5 0 0 0 0 0 1 0 0 0 0 0 0
$tail_A
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
[175,] 174 0 0 0 0 0 0 1 0 0 0 0 0
[176,] 175 0 0 0 0 0 0 0 1 0 0 0 0
[177,] 176 0 0 0 0 0 0 0 0 1 0 0 0
[178,] 177 0 0 0 0 0 0 0 0 0 1 0 0
[179,] 178 0 0 0 0 0 0 0 0 0 0 1 0
[180,] 179 0 0 0 0 0 0 0 0 0 0 0 1
$dim_A
[1] 180 13y <- t(vmt) %>%
as.vector() %>%
matrix(ncol = 1)
list(head_y = head(y), tail_y = tail(y))$head_y
[,1]
[1,] 203442
[2,] 199261
[3,] 232490
[4,] 227698
[5,] 242501
[6,] 242963
$tail_y
[,1]
[175,] 272335
[176,] 271018
[177,] 249125
[178,] 267185
[179,] 242816
[180,] 253618QR <- qr(x = A)
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
b <- t(Q) %*% y
x_hat <- solve(a = R) %*% b
list(Q = dim(Q), R = dim(R), b = dim(b), x_hat = dim(x_hat))$Q
[1] 180 13
$R
[1] 13 13
$b
[1] 13 1
$x_hat
[1] 13 1Date <- seq(as.Date("2000-1-1"), as.Date("2014-12-1"), by = "+1 month")
ggplot(mapping = aes(x = Date)) +
geom_point(mapping = aes(y = y)) +
geom_line(mapping = aes(y = y)) +
geom_line(mapping = aes(y = A %*% x_hat), col = "red") +
labs(x = "", y = "Vehicle miles traveled in the US, per month")Polynomial fit. (p.255)
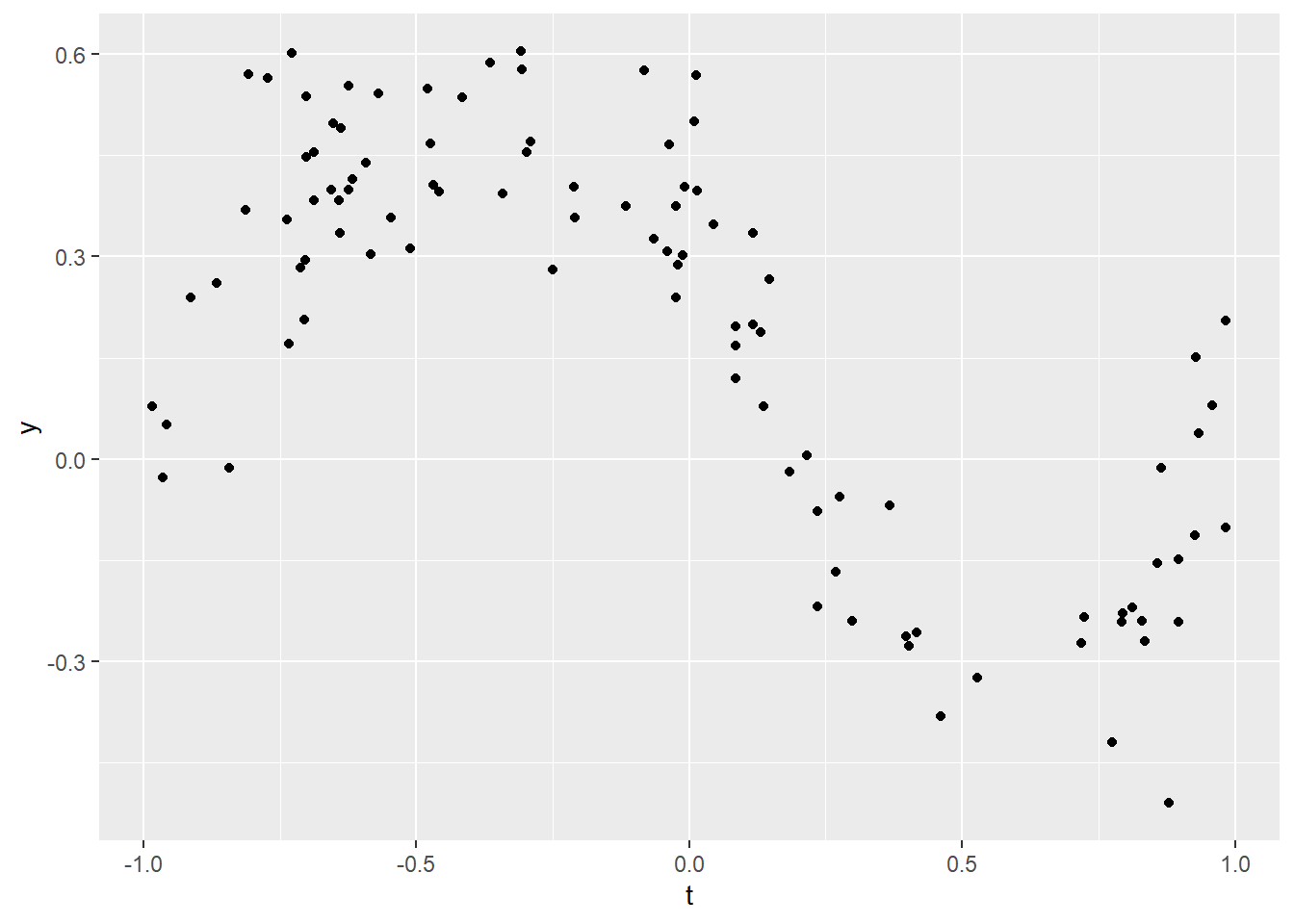
# サンプルデータ
m <- 100
t <- -1 + 2 * runif(n = m)
y <- t^3 - t + 0.4 / (1 + 25 * t^2) + 0.10 * rnorm(n = m)
ggplot(mapping = aes(x = t, y = y)) +
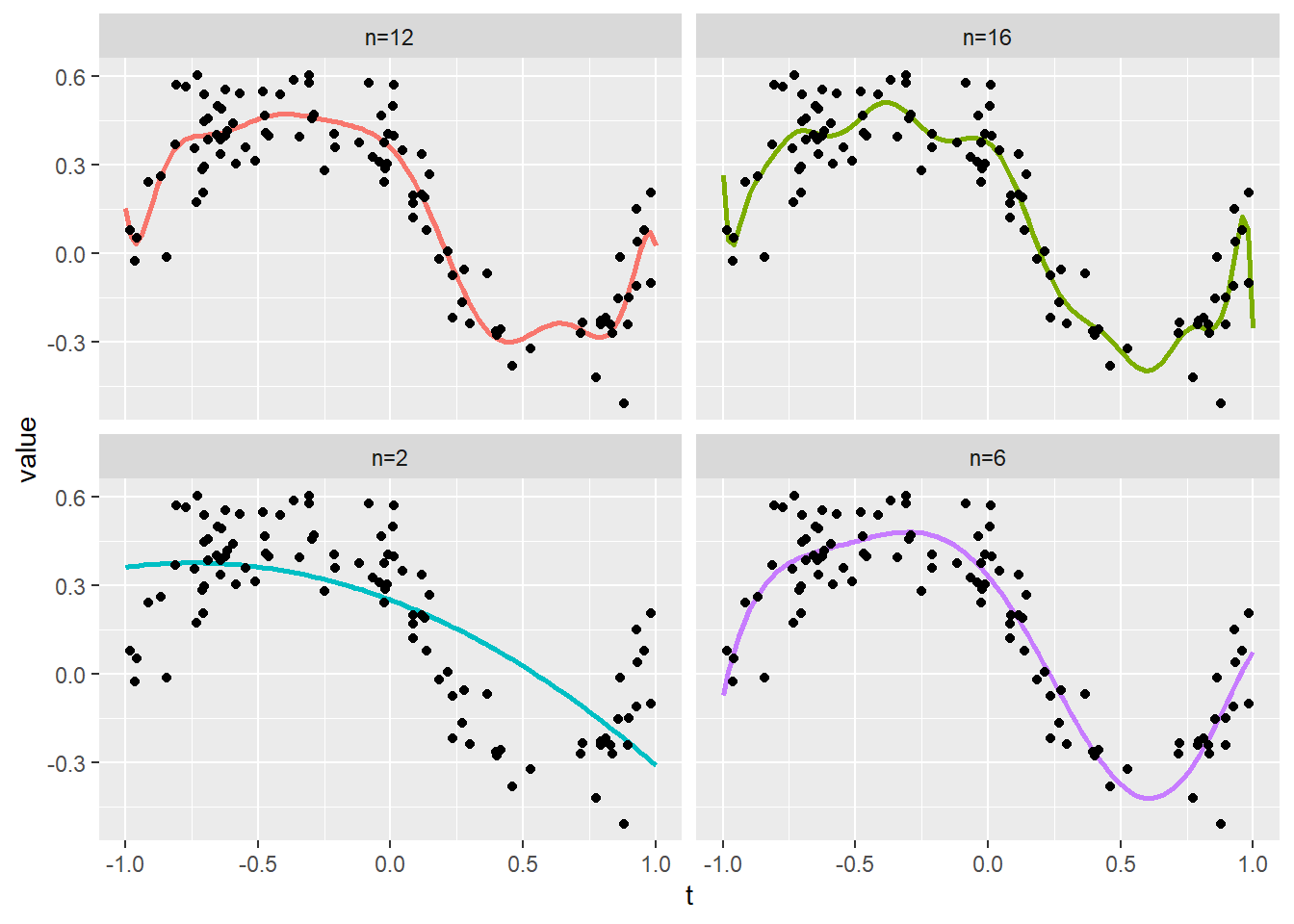
geom_point()# 多項式回帰関数
func_polynomial_regression <- function(n, t, y, t_plot) {
# https://stackoverflow.com/questions/61207545/create-a-vandermonde-matrix-in-r
vandermonde_matrix <- outer(X = t, Y = seq(n + 1) - 1, FUN = "^")
#
QR <- qr(x = vandermonde_matrix)
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
b <- t(Q) %*% y
x_hat <- solve(a = R) %*% b
#
polyeval <- outer(X = t_plot, Y = seq(length(x_hat)) - 1, FUN = "^") %*% x_hat
return(polyeval)
}# 対象多項式次数
n <- c(2, 6, 12, 16)# プロット
t_plot <- seq(-1, 1, length.out = 100)
polyeval <- sapply(n, function(x) func_polynomial_regression(n = x, y = y, t_plot = t_plot, t = t)) %>%
data.frame(t = t_plot, .)
colnames(polyeval)[-1] <- paste0("n=", n)
tidydf <- gather(data = polyeval, key = "key", value = "value", colnames(polyeval)[-1])
pointdf <- data.frame(t, y)
ggplot() +
geom_line(data = tidydf, mapping = aes(x = t, y = value, color = key), size = 1) +
facet_wrap(facets = ~key, nrow = 2, scales = "fixed") +
geom_point(data = pointdf, mapping = aes(x = t, y = y)) +
theme(legend.position = "none") +
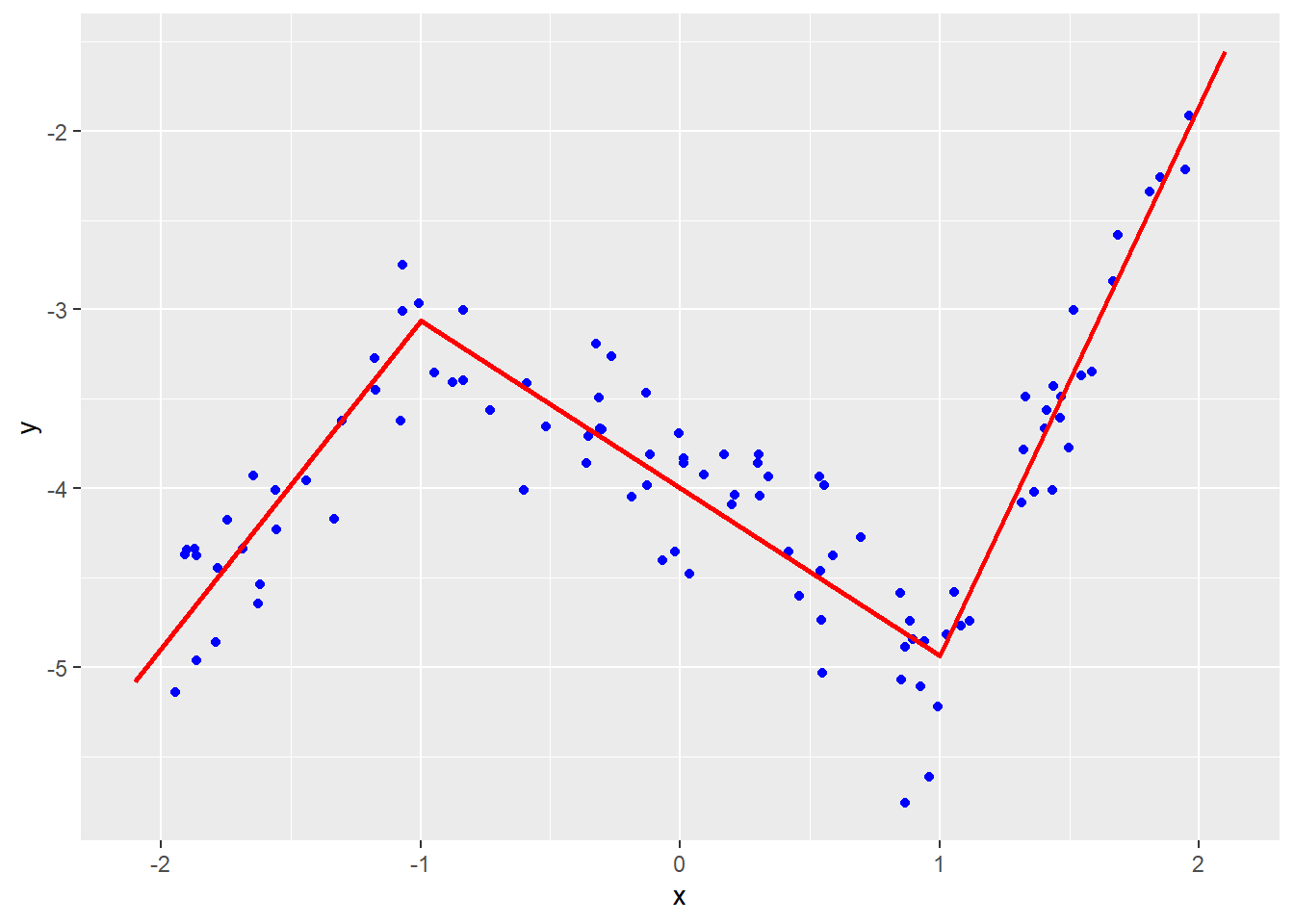
ylim(range(pointdf$y))Piecewise-linear fit. (p.256)
# サンプルデータ
m <- 100
x <- -2 + 4 * runif(n = m)
tmp1 <- sapply(X = x, function(x) max(x + 1, 0))
tmp2 <- sapply(X = x, function(x) max(x - 1, 0))
y <- 1 + 2 * (x - 1) - 3 * tmp1 + 4 * tmp2 + 0.3 * rnorm(n = m)# 区分線形関数
A <- cbind(rep(1, m), x, tmp1, tmp2)
QR <- qr(x = A)
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
b <- t(Q) %*% y
x_hat <- solve(a = R) %*% b
t <- c(-2.1, -1, 1, 2.1)
y_hat <-
x_hat[1] +
x_hat[2] * t +
x_hat[3] * sapply(X = t + 1, FUN = function(x) max(x, 0)) +
x_hat[4] * sapply(X = t - 1, FUN = function(x) max(x, 0))
ggplot() +
geom_point(mapping = aes(x = x, y = y), color = "blue") +
geom_line(mapping = aes(x = t, y = y_hat), color = "red", size = 1)13 Least squares data fitting > 13.1 Least squares data fitting > 13.1.2 Regression (p.257)
House price regression. (p.258)
# 重回帰分析
list(area = summary(area), beds = table(beds), price = summary(price))$area
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.539 1.146 1.419 1.583 1.836 4.303
$beds
beds
1 2 3 4 5 6
8 116 380 223 46 1
$price
Min. 1st Qu. Median Mean 3rd Qu. Max.
55.42 150.00 208.00 228.77 284.84 699.00 # 係数の推定
m <- length(price)
A <- cbind(constant = rep(1, m), area, beds)
QR <- qr(x = A)
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
b <- t(Q) %*% price
x_hat <- solve(a = R) %*% b
x_hat [,1]
constant 54.40167
area 148.72507
beds -18.85336# 誤差の二乗平均平方根(RMS)
(sum((price - A %*% x_hat)^2) / m)^0.5[1] 74.84572# 標本標準偏差
sqrt(var(price) * (length(price) - 1) / length(price))[1] 112.7822Auto-regressive time series model. (p.259)
# サンプルデータ
library(ggplot2)
summary(t)
N <- length(t) Min. 1st Qu. Median Mean 3rd Qu. Max.
54.00 59.00 61.00 61.76 64.00 70.00 # 標準偏差
sqrt(var(t) * (length(t) - 1) / length(t))[1] 3.050559# ラグ次数=1の場合の二乗平均平方根
{
sum((tail(t, -1) - head(t, -1))^2) / (N - 1)
}^0.5[1] 1.160243# ラグ次数=24の場合の二乗平均平方根
{
sum((tail(t, -24) - head(t, -24))^2) / (N - 24)
}^0.5[1] 1.733894# 自己回帰ラグ次数を 8 とした最小二乗法
M <- 8
y <- tail(t, -M)
A <- sapply(rev(seq(M)), function(i) t[i:(i + N - M - 1)])
list(dim_A = dim(A), head_A = head(A), tail_A = tail(A))$dim_A
[1] 736 8
$head_A
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,] 60.1 57.0 57.0 55.9 57.0 57.0 57.9 59.0
[2,] 62.1 60.1 57.0 57.0 55.9 57.0 57.0 57.9
[3,] 64.0 62.1 60.1 57.0 57.0 55.9 57.0 57.0
[4,] 64.9 64.0 62.1 60.1 57.0 57.0 55.9 57.0
[5,] 66.0 64.9 64.0 62.1 60.1 57.0 57.0 55.9
[6,] 69.1 66.0 64.9 64.0 62.1 60.1 57.0 57.0
$tail_A
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[731,] 63.0 64.9 66.0 68.0 68.0 68.0 64.9 63.0
[732,] 62.1 63.0 64.9 66.0 68.0 68.0 68.0 64.9
[733,] 62.1 62.1 63.0 64.9 66.0 68.0 68.0 68.0
[734,] 62.1 62.1 62.1 63.0 64.9 66.0 68.0 68.0
[735,] 62.1 62.1 62.1 62.1 63.0 64.9 66.0 68.0
[736,] 62.1 62.1 62.1 62.1 62.1 63.0 64.9 66.0# QR分解による最小二乗法
QR <- qr(x = A)
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
b <- t(Q) %*% y
x_hat <- solve(a = R) %*% b
y_predict <- A %*% x_hat
list(x_hat = x_hat)$x_hat
[,1]
[1,] 1.233765489
[2,] 0.007910523
[3,] -0.214893749
[4,] 0.043416077
[5,] -0.118176365
[6,] -0.131813798
[7,] 0.091479893
[8,] 0.088167609# 予測誤差の二乗平均平方根
(sum((y_predict - y)^2) / length(y))^0.5[1] 1.01296313 Least squares data fitting > 13.2. Validation (p.260)
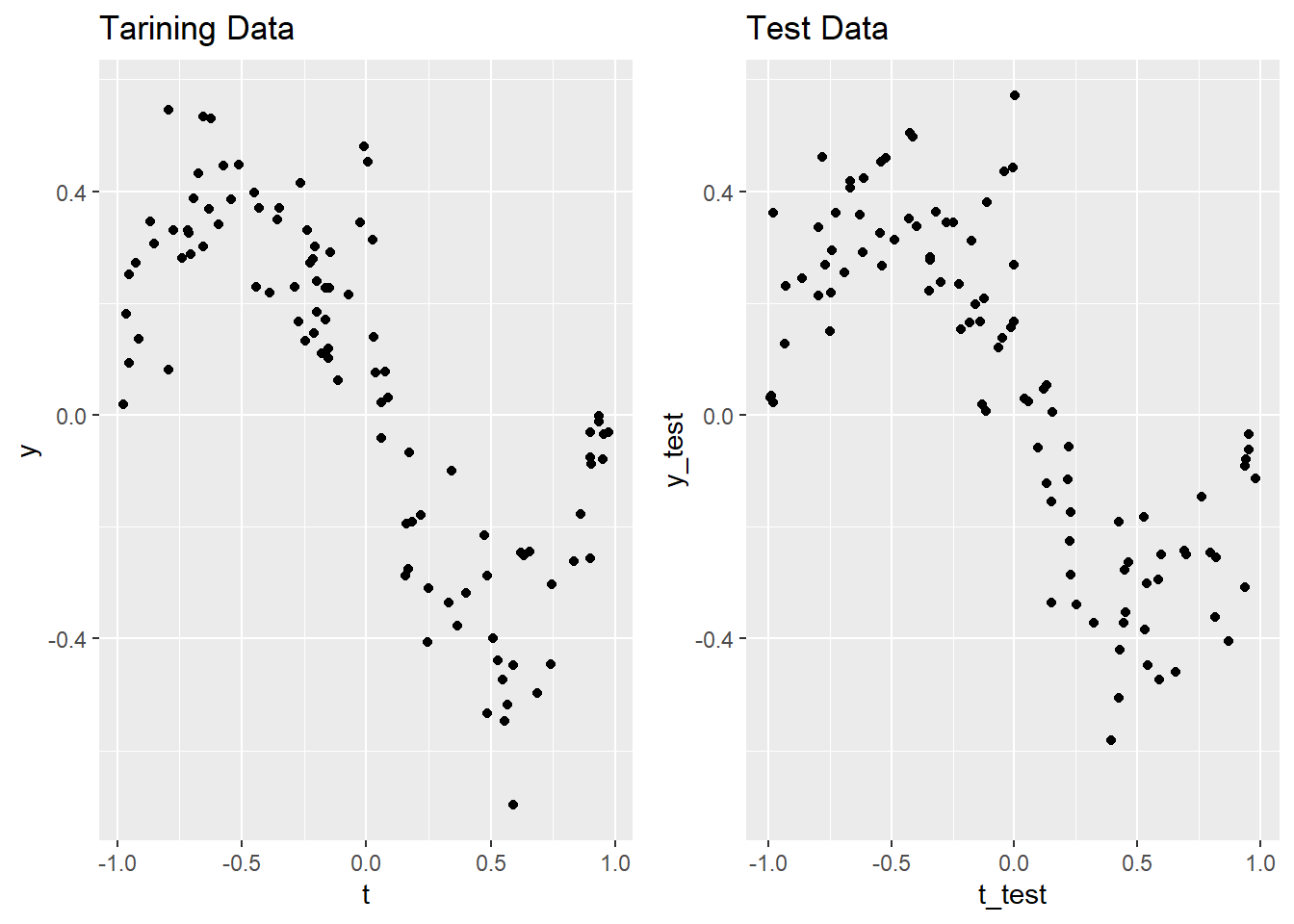
Example. (p.263)
library(dplyr)
library(ggplot2)
library(tidyr)
library(gridExtra)
# サンプルデータ作成
func_generate_sample <- function(m) {
t <- -1 + 2 * runif(n = m)
y <- t^3 - t + 0.4 / (1 + (25 * t)^2) + 0.10 * rnorm(n = m)
return(list(t = t, y = y))
}
m <- 100
tmp <- func_generate_sample(m = m)
t <- tmp$t
y <- tmp$y
tmp <- func_generate_sample(m = m)
t_test <- tmp$t
y_test <- tmp$yg <- list()
g[[1]] <- ggplot(mapping = aes(x = t, y = y)) +
geom_point() +
labs(title = "Tarining Data") +
ylim(range(y, y_test))
g[[2]] <- ggplot(mapping = aes(x = t_test, y = y_test)) +
geom_point() +
labs(title = "Test Data") +
ylim(range(y, y_test))
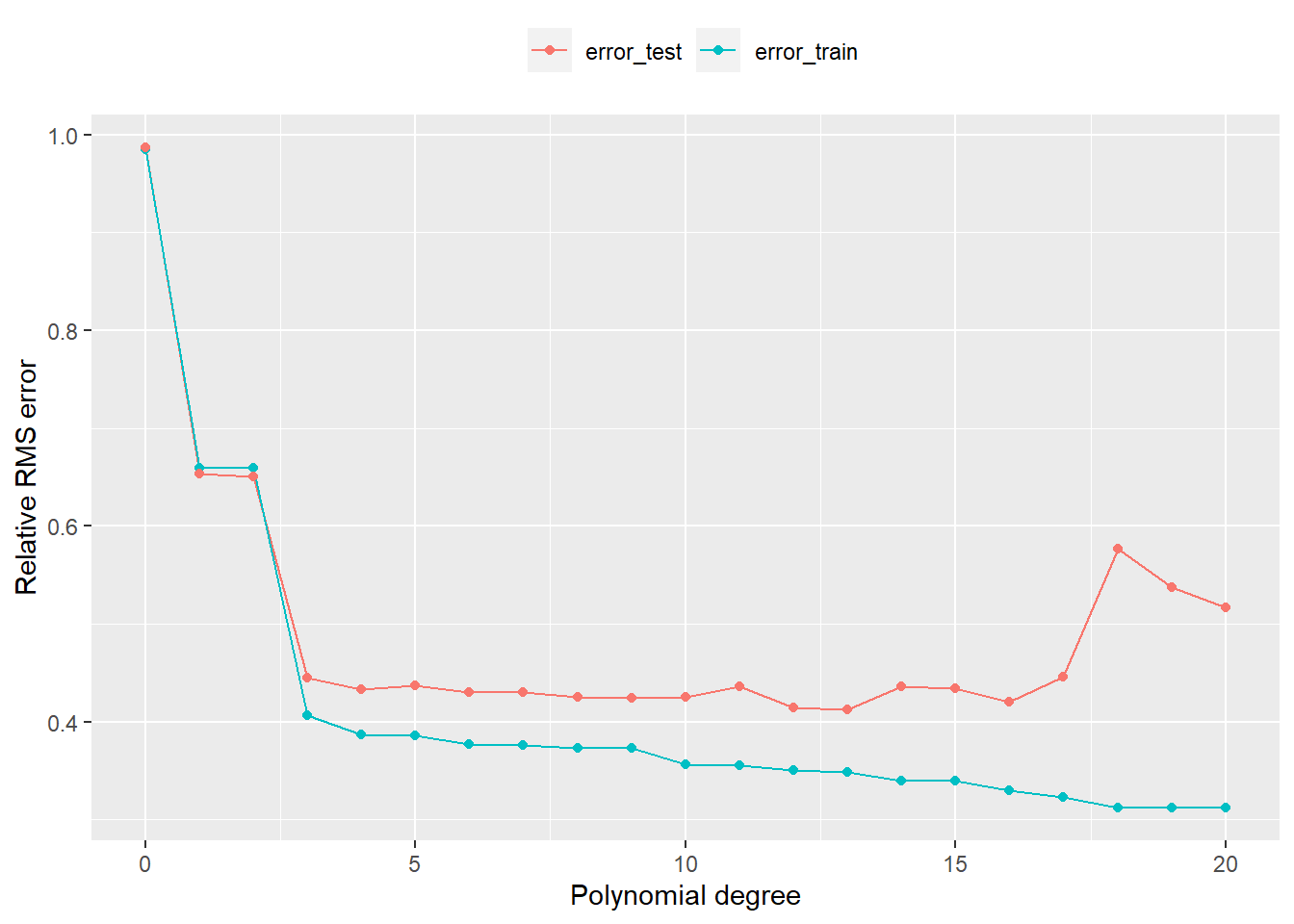
arrangeGrob(grobs = g, ncol = 2, nrow = 1, widths = c(1, 1)) %>% ggpubr::as_ggplot()error_train <- error_test <- vector()
for (p in 1:21) {
A <- outer(X = t, Y = seq(p) - 1, FUN = "^")
A_test <- outer(X = t_test, Y = seq(p) - 1, FUN = "^")
QR <- qr(x = A)
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
b <- t(Q) %*% y
x_hat <- solve(a = R) %*% b
error_train[p] <- norm(x = A %*% x_hat - matrix(y, ncol = 1), type = "2") /
norm(x = y, type = "2")
error_test[p] <- norm(x = A_test %*% x_hat - matrix(y_test, ncol = 1), type = "2") /
norm(x = y_test, type = "2")
}
data.frame(`polynomial degree` = seq(p) - 1, error_train, error_test, check.names = F) %>%
gather(key = "key", value = "value", colnames(.)[-1]) %>%
ggplot(mapping = aes(x = .[, 1], y = .[, 3], color = .[, 2])) +
geom_line() +
geom_point() +
labs(x = "Polynomial degree", y = "Relative RMS error") +
theme(legend.title = element_blank(), legend.position = "top")House price regression model. (p.265)
# 重回帰分析
list(
baths = table(baths), location = table(location), price = summary(price),
beds = table(beds), area = summary(area), condo = table(condo)
)$baths
baths
1 2 3 4 5
166 493 106 8 1
$location
location
1 2 3 4
26 340 338 70
$price
Min. 1st Qu. Median Mean 3rd Qu. Max.
55.42 150.00 208.00 228.77 284.84 699.00
$beds
beds
1 2 3 4 5 6
8 116 380 223 46 1
$area
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.539 1.146 1.419 1.583 1.836 4.303
$condo
condo
0 1
735 39 N <- length(price)
X <- cbind(rep(1, length(price)), area, beds)
split_n <- 5
I <- sample(x = seq(N), size = N, replace = F) %>% split(f = 1:split_n)
rms_train <- rms_test <- vector()
coeff <- matrix()
result_train <- result_test <- list()
for (k in seq(split_n)) {
Itest <- I[[k]]
Itrain <- sapply(setdiff(seq(split_n), k), function(x) I[[x]]) %>% Reduce(function(x, y) c(x, y), .)
#
QR <- qr(x = X[Itrain, ])
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
b <- t(Q) %*% price[Itrain]
x_hat <- solve(a = R) %*% b
x_hat
#
if (k == 1) {
coeff <- x_hat %>% t()
} else {
coeff <- rbind(coeff, x_hat %>% t())
}
rms_train[k] <- (sum((X[Itrain, ] %*% x_hat - price[Itrain])^2) / N)^0.5
rms_test[k] <- (sum((X[Itest, ] %*% x_hat - price[Itest])^2) / N)^0.5
tmp01 <- data.frame(price[Itrain], X[Itrain, ] %*% x_hat)
colnames(tmp01) <- c("Actual Price for training", "Predicted price(Training)")
result_train[[k]] <- tmp01
head(tmp01) %>% print()
tmp02 <- data.frame(price[Itest], X[Itest, ] %*% x_hat)
colnames(tmp02) <- c("Actual Price for test", "Predicted price(Test)")
result_test[[k]] <- tmp02
head(tmp02) %>% print()
}
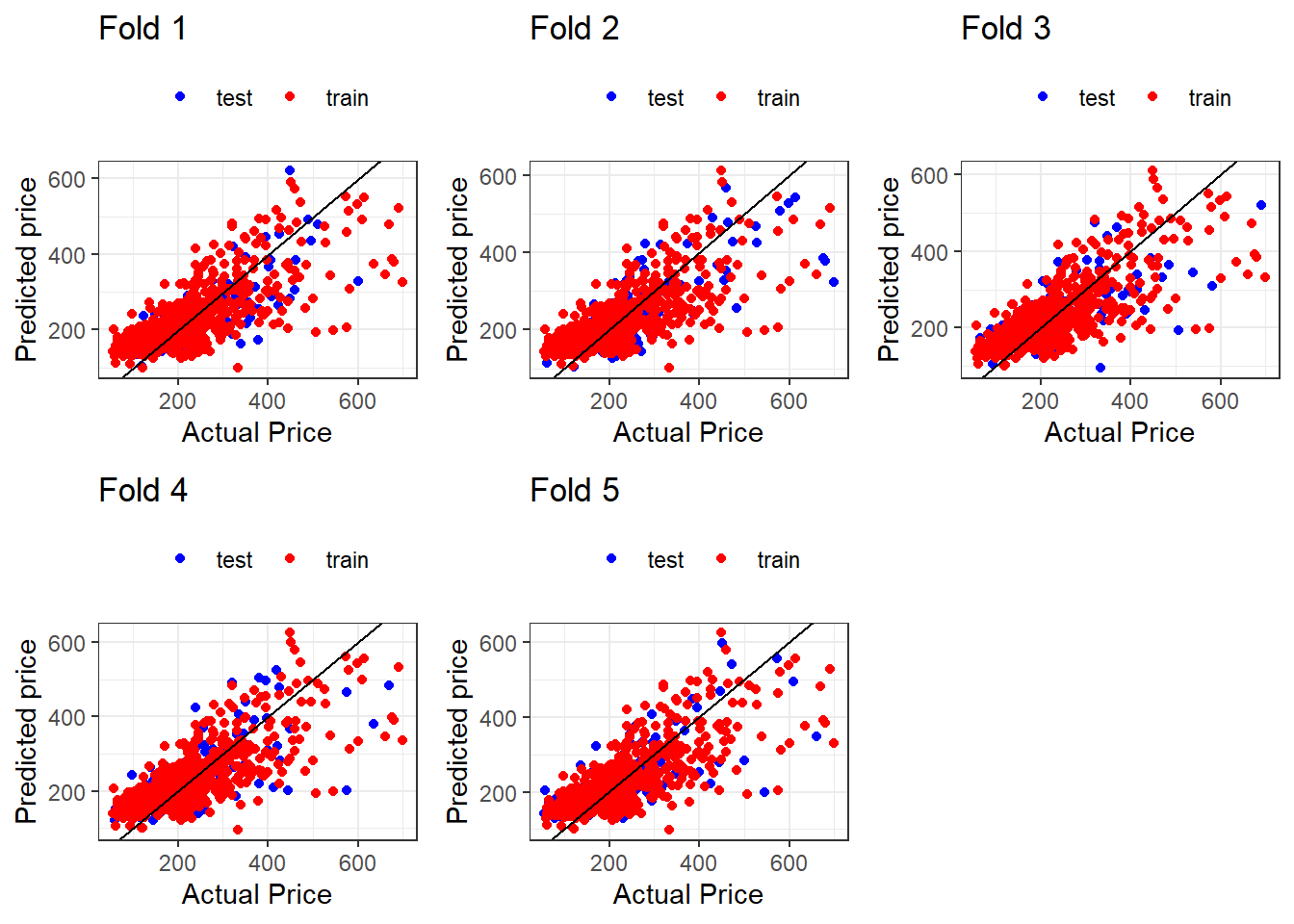
colnames(coeff)[1] <- "constant"coeff constant area beds
[1,] 59.84812 150.3868 -21.52018
[2,] 62.51126 146.9928 -20.71722
[3,] 46.17634 144.4939 -14.61995
[4,] 46.62748 150.1279 -16.72811
[5,] 57.01122 151.2613 -20.57694cbind(rms_train, rms_test) rms_train rms_test
[1,] 68.71690 29.71196
[2,] 66.59759 34.24948
[3,] 66.60560 34.24997
[4,] 66.03077 35.35007
[5,] 66.57772 34.23061func_plot <- function(k) {
g <- ggplot() +
geom_point(mapping = aes(x = result_test[[k]][, 1], y = result_test[[k]][, 2], color = "test")) +
geom_point(mapping = aes(x = result_train[[k]][, 1], y = result_train[[k]][, 2], color = "train")) +
geom_abline(intercept = 0, slope = 1) +
labs(title = paste("Fold", k), x = "Actual Price", y = "Predicted price") +
scale_color_manual(values = c("test" = "blue", "train" = "red")) +
theme_bw() +
theme(legend.title = element_blank(), legend.position = "top")
return(g)
}
g <- list()
for (k in seq(split_n)) {
g[[k]] <- func_plot(k = k)
}
arrangeGrob(grobs = g, ncol = 3, widths = c(1, 1, 1)) %>% ggpubr::as_ggplot()Validating time series predictions. (p.266)
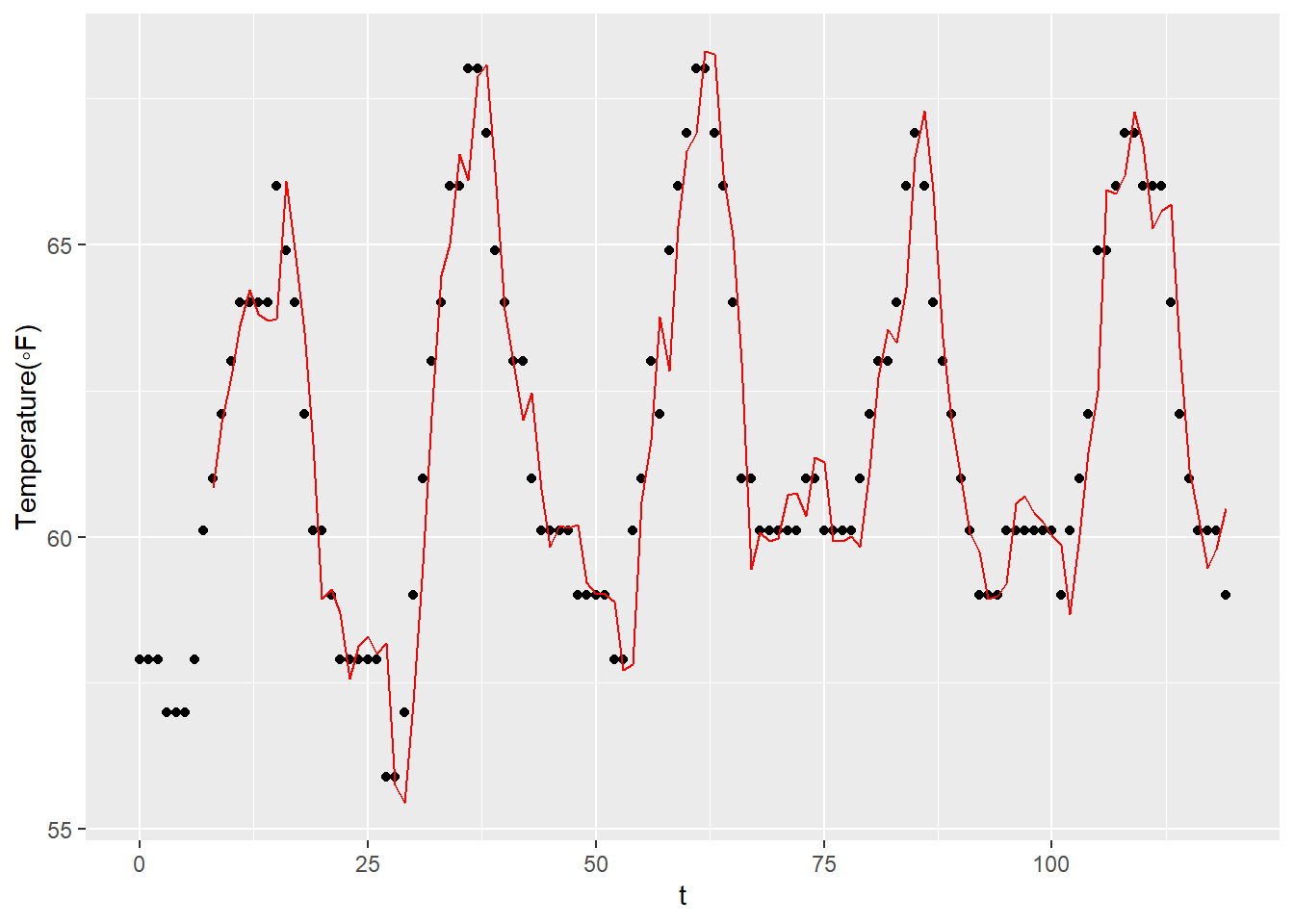
# サンプルデータ
summary(t) Min. 1st Qu. Median Mean 3rd Qu. Max.
54.00 59.00 61.00 61.76 64.00 70.00 N <- length(t)
# 最初の24日分(24日×24時間)のデータを訓練データとして利用
Ntrain <- 24 * 24
t_train <- t %>% head(Ntrain) # ;head(t_train);tail(t_train)
t_test <- t %>% tail(-Ntrain) # ;head(t_test);tail(t_test)
# 自己回帰のラグ次数を 8 とした線形回帰
M <- 8
m <- Ntrain - M
y <- t_train %>% tail(-M)
A <- sapply(rev(seq(M)), function(i) t[c(i:(i + m - 1))]) # ;head(A);tail(A)
#
QR <- qr(x = A)
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
b <- t(Q) %*% y
x_hat <- solve(a = R) %*% b
rms_train <- (sum((A %*% x_hat - y)^2) / length(y))^0.5
ytest <- t_test %>% tail(-M)
mtest <- length(ytest)
ypred <- sapply(rev(seq(M)), function(i) t_test[c(i:(i + mtest - 1))]) %*% x_hat
rms_test <- (sum((ypred - ytest)^2) / length(ytest))^0.5
list(x_hat = x_hat, rms_test = rms_test, rms_train = rms_train)$x_hat
[,1]
[1,] 1.20868426
[2,] 0.05067080
[3,] -0.23411924
[4,] 0.05710085
[5,] -0.14244840
[6,] -0.14097707
[7,] 0.13142279
[8,] 0.06944674
$rms_test
[1] 0.9755114
$rms_train
[1] 1.02535813 Least squares data fitting > 13.3. Feature engineering > 13.3.5 House price prediction (p.274)
The resulting model. (p.275)
# 重回帰分析
list(
baths = table(baths), location = table(location), price = summary(price),
beds = table(beds), area = summary(area), condo = table(condo)
)$baths
baths
1 2 3 4 5
166 493 106 8 1
$location
location
1 2 3 4
26 340 338 70
$price
Min. 1st Qu. Median Mean 3rd Qu. Max.
55.42 150.00 208.00 228.77 284.84 699.00
$beds
beds
1 2 3 4 5 6
8 116 380 223 46 1
$area
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.539 1.146 1.419 1.583 1.836 4.303
$condo
condo
0 1
735 39 N <- length(price)
X <- cbind(
constant = rep(1, N),
area,
`area exceeds 1.5` = sapply(area - 1.5, function(x) max(x, 0)),
beds,
condo,
location2 = {
location == 2
} %>% as.numeric(),
location3 = {
location == 3
} %>% as.numeric(),
location4 = {
location == 4
} %>% as.numeric()
)
QR <- qr(x = X)
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
b <- t(Q) %*% price
x_hat <- solve(a = R) %*% b
x_hat [,1]
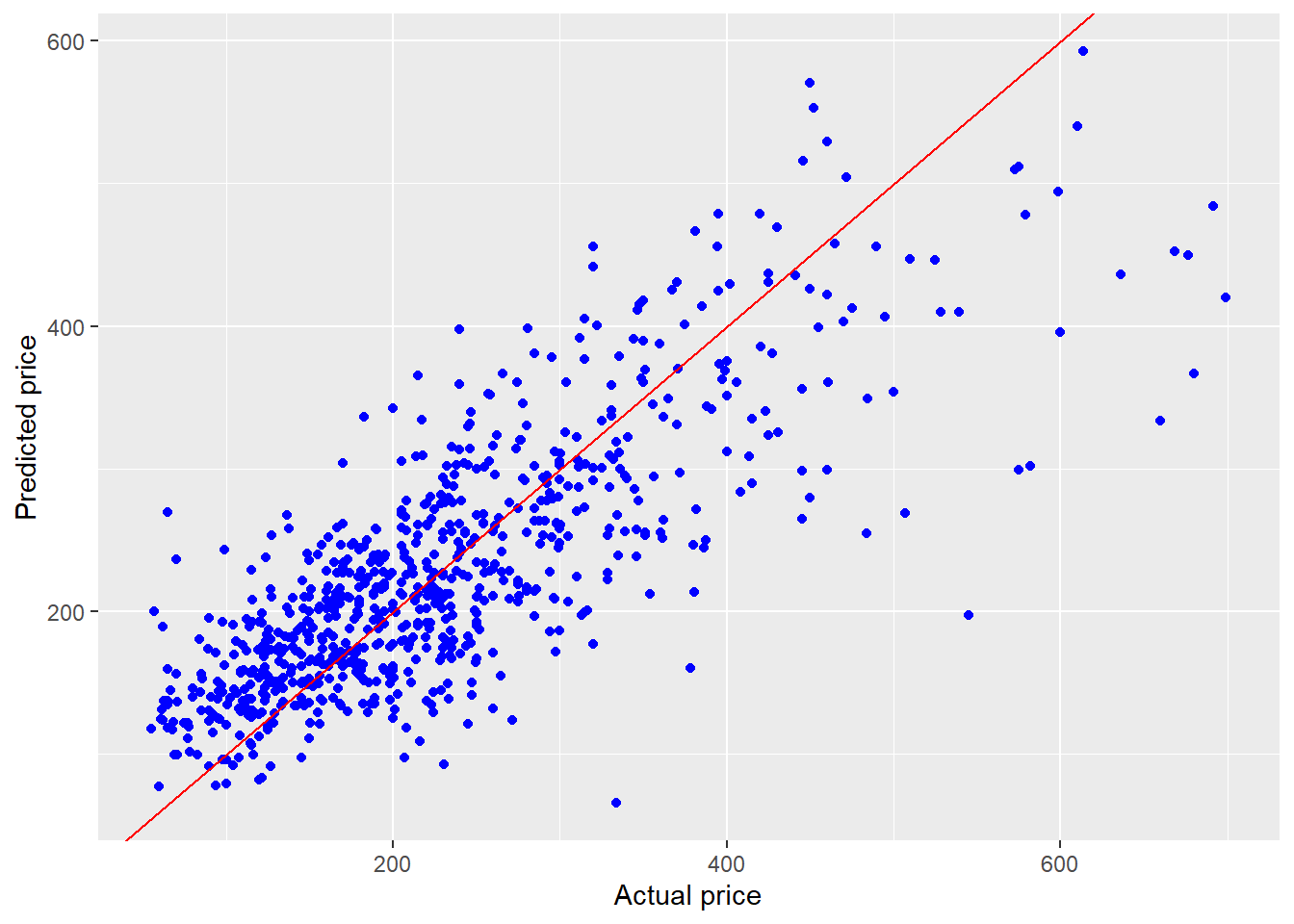
constant 115.61682
area 175.41314
area exceeds 1.5 -42.74777
beds -17.87836
condo -19.04473
location2 -100.91050
location3 -108.79112
location4 -24.76525# 予測値のRMS
(sum((X %*% x_hat - price)^2) / N)^0.5[1] 68.34429ggplot() +
geom_point(mapping = aes(x = price, y = X %*% x_hat), color = "blue") +
geom_abline(intercept = 0, slope = 1, color = "red") +
labs(x = "Actual price", y = "Predicted price")split_n <- 5
I <- sample(x = seq(N), size = N, replace = F) %>% split(f = 1:split_n)
rms_train <- rms_test <- vector()
coeff <- matrix()
result_train <- result_test <- list()
for (k in seq(split_n)) {
Itest <- I[[k]]
Itrain <- sapply(setdiff(seq(split_n), k), function(x) I[[x]]) %>% Reduce(function(x, y) c(x, y), .)
#
QR <- qr(x = X[Itrain, ])
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
b <- t(Q) %*% price[Itrain]
x_hat <- solve(a = R) %*% b
x_hat
#
if (k == 1) {
coeff <- x_hat %>% t()
} else {
coeff <- rbind(coeff, x_hat %>% t())
}
rms_train[k] <- (sum((X[Itrain, ] %*% x_hat - price[Itrain])^2) / N)^0.5
rms_test[k] <- (sum((X[Itest, ] %*% x_hat - price[Itest])^2) / N)^0.5
tmp01 <- data.frame(price[Itrain], X[Itrain, ] %*% x_hat)
colnames(tmp01) <- c("Actual Price for training", "Predicted price(Training)")
result_train[[k]] <- tmp01
head(tmp01) %>% print()
tmp02 <- data.frame(price[Itest], X[Itest, ] %*% x_hat)
colnames(tmp02) <- c("Actual Price for test", "Predicted price(Test)")
result_test[[k]] <- tmp02
head(tmp02) %>% print()
}
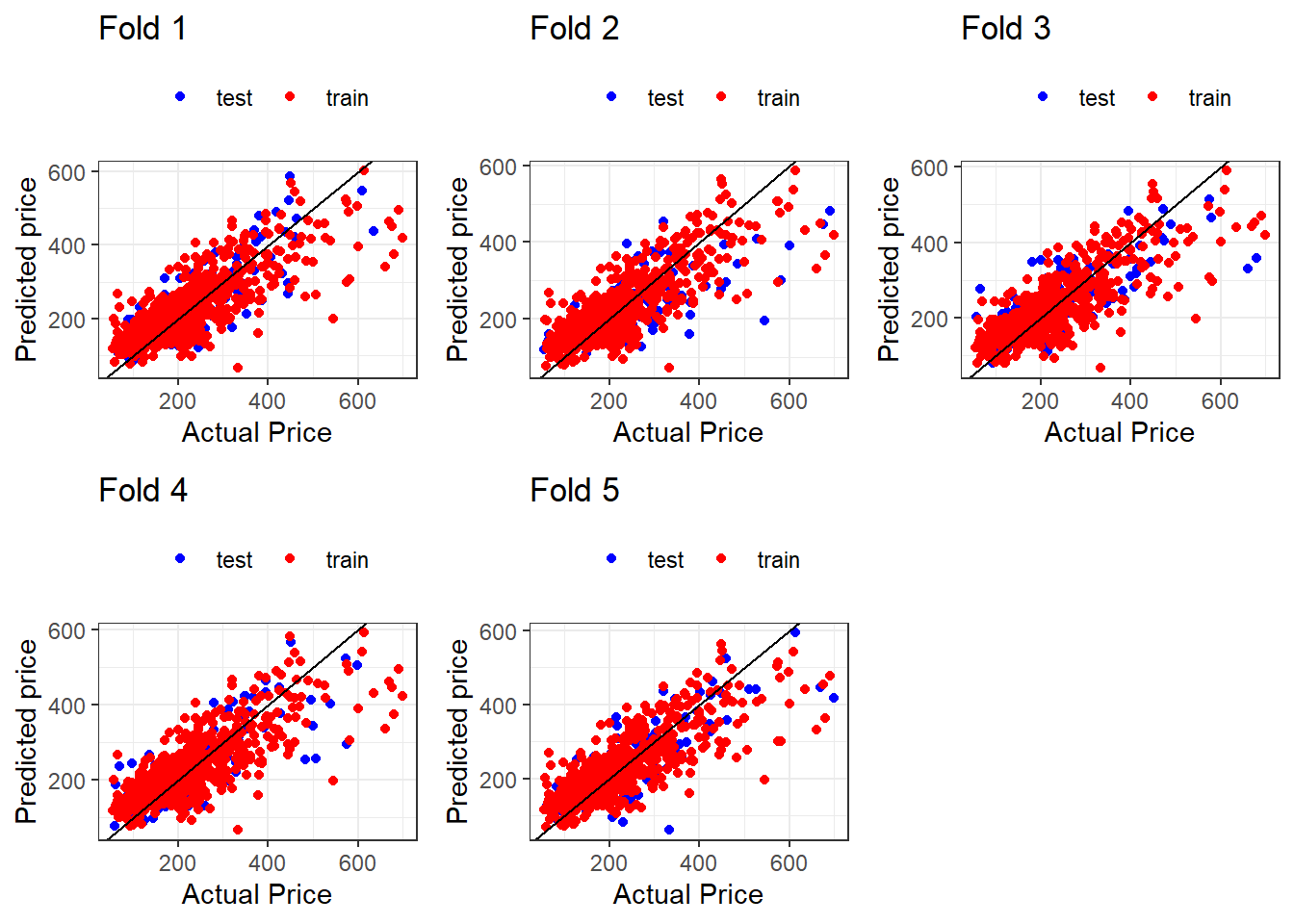
colnames(coeff)[1] <- "constant"coeff constant area area exceeds 1.5 beds condo location2
[1,] 113.7676 178.6647 -39.56686 -19.70668 -14.71673 -96.28126
[2,] 123.3538 163.4534 -31.54539 -15.86756 -21.35463 -100.51723
[3,] 122.0812 179.1469 -52.46999 -19.06668 -19.10166 -107.97952
[4,] 112.6868 172.4583 -35.89811 -16.51583 -17.39511 -98.54583
[5,] 107.2806 184.2586 -54.30090 -18.71864 -23.81243 -102.39729
location3 location4
[1,] -105.7506 -26.00201
[2,] -109.4503 -26.71720
[3,] -113.8584 -20.72117
[4,] -106.4789 -33.09194
[5,] -108.9944 -18.19249cbind(rms_train, rms_test) rms_train rms_test
[1,] 63.14063 26.41506
[2,] 58.52871 35.42335
[3,] 60.07720 32.89232
[4,] 61.62543 29.78823
[5,] 61.73048 29.50860func_plot <- function(k) {
g <- ggplot() +
geom_point(mapping = aes(x = result_test[[k]][, 1], y = result_test[[k]][, 2], color = "test")) +
geom_point(mapping = aes(x = result_train[[k]][, 1], y = result_train[[k]][, 2], color = "train")) +
geom_abline(intercept = 0, slope = 1) +
labs(title = paste("Fold", k), x = "Actual Price", y = "Predicted price") +
scale_color_manual(values = c("test" = "blue", "train" = "red")) +
theme_bw() +
theme(legend.title = element_blank(), legend.position = "top")
return(g)
}
g <- list()
for (k in seq(split_n)) {
g[[k]] <- func_plot(k = k)
}
arrangeGrob(grobs = g, ncol = 3, widths = c(1, 1, 1)) %>% ggpubr::as_ggplot()14 Least squares classification > 14.2. Least squares classifier > 14.2.1 Iris flower classification (p.289)
data("iris")iris$Species %>% unique()[1] setosa versicolor virginica
Levels: setosa versicolor virginicalapply(iris$Species %>% unique(), function(x) iris[x == iris$Species, ] %>% nrow())[[1]]
[1] 50
[[2]]
[1] 50
[[3]]
[1] 50# setosa または versicolor:-1、virginica:1
y <- c(rep(-1, 50 * 2), rep(1, 50))
A <- cbind(constant = rep(1, 50 * 3), iris[, -5])
QR <- qr(x = A)
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
# setosa または versicolor:-1、virginica:1
b <- t(Q) %*% y
x_hat <- solve(a = R) %*% b
x_hat [,1]
constant -2.390563727
Sepal.Length -0.091752169
Sepal.Width 0.405536771
Petal.Length 0.007975822
Petal.Width 1.103558650# 混同行列
# 予測結果が 0 を超えている場合を TRUE、0 以下の場合を FALSE とする。
yhat <- {
A %>% as.matrix(ncol = 5)
} %*% {
x_hat %>% matrix(ncol = 1)
} > 0
result <- matrix(nrow = 3, ncol = 3)
result[1, 1] <- {
{
y > 0
} & yhat
} %>% sum()
result[1, 2] <- {
{
y > 0
} & !yhat
} %>% sum()
result[2, 1] <- {
{
y <= 0
} & yhat
} %>% sum()
result[2, 2] <- {
{
y <= 0
} & !yhat
} %>% sum()
result[1, 3] <- sum(result[1, ], na.rm = T)
result[2, 3] <- sum(result[2, ], na.rm = T)
result[3, 1] <- sum(result[, 1], na.rm = T)
result[3, 2] <- sum(result[, 2], na.rm = T)
result[3, 3] <- sum(result[, 3], na.rm = T)
result [,1] [,2] [,3]
[1,] 46 4 50
[2,] 7 93 100
[3,] 53 97 150# エラーレート(混同行列より)
(result[2, 1] + result[1, 2]) / result[3, 3] * 100[1] 7.333333# エラーレート(直接)
{
{
y > 0
} != yhat
} %>%
{
sum(.) / length(.)
} * 100[1] 7.33333315 Multi-objective least squares > 15.1 Multi-objective least squares (p.309)
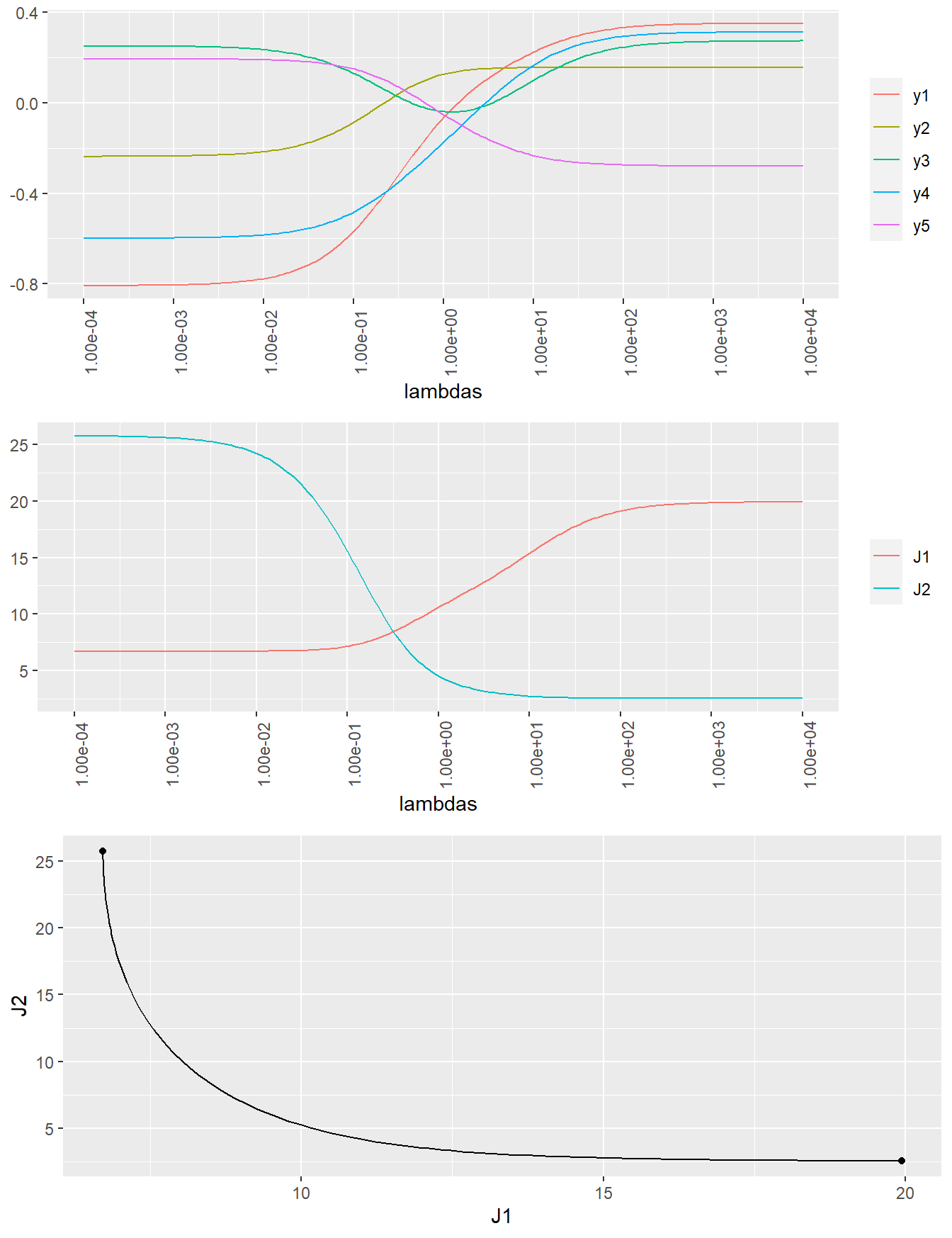
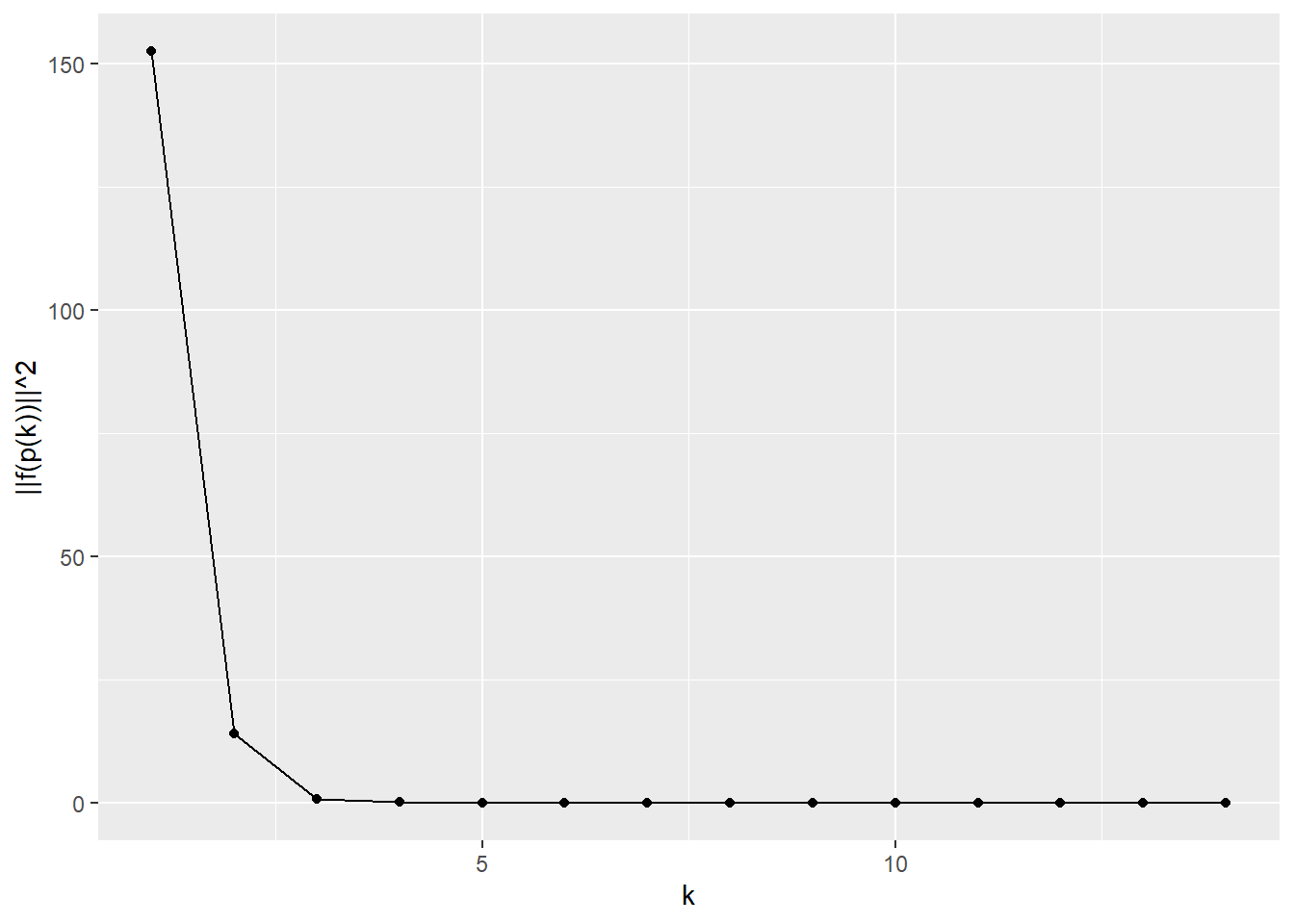
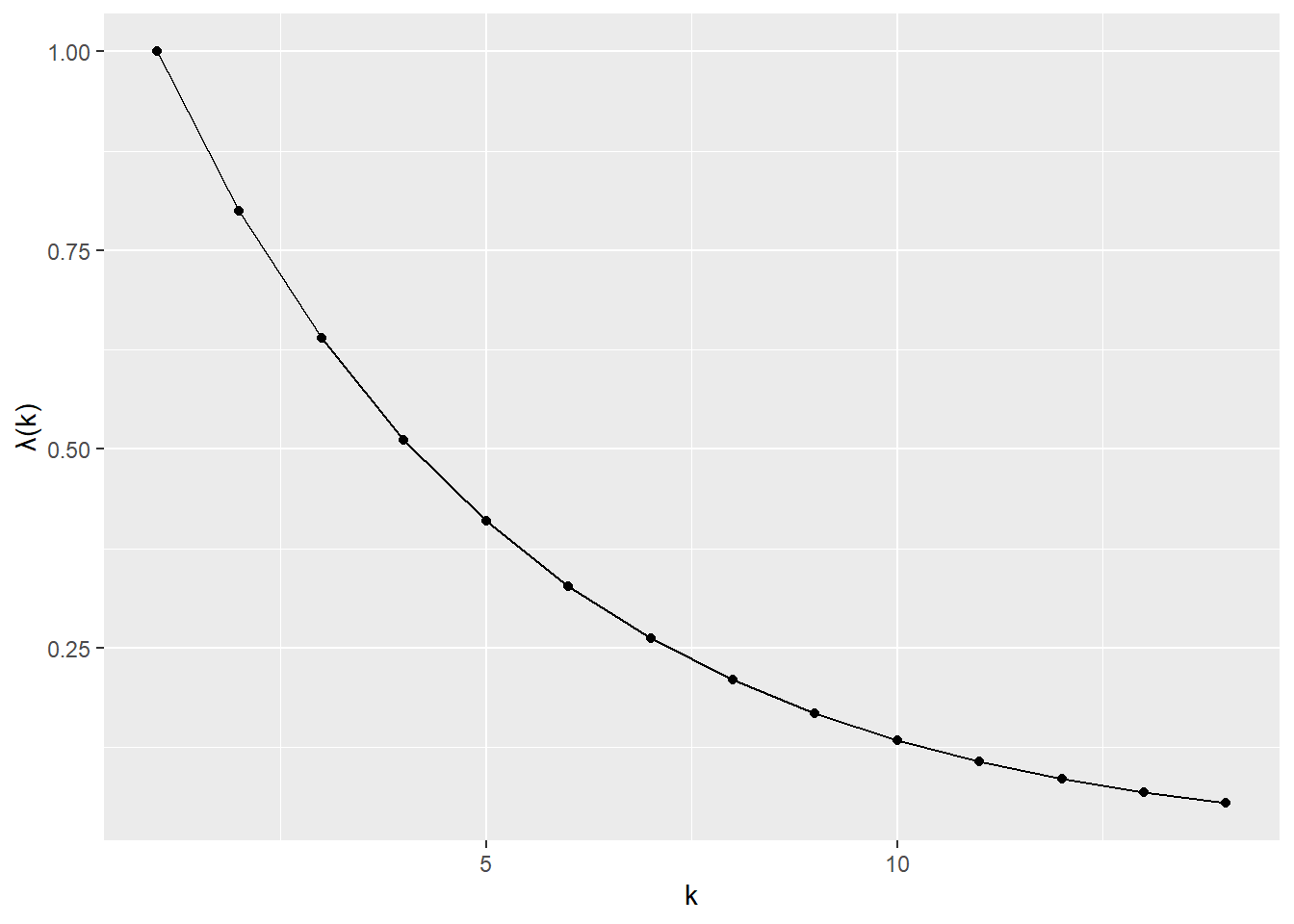
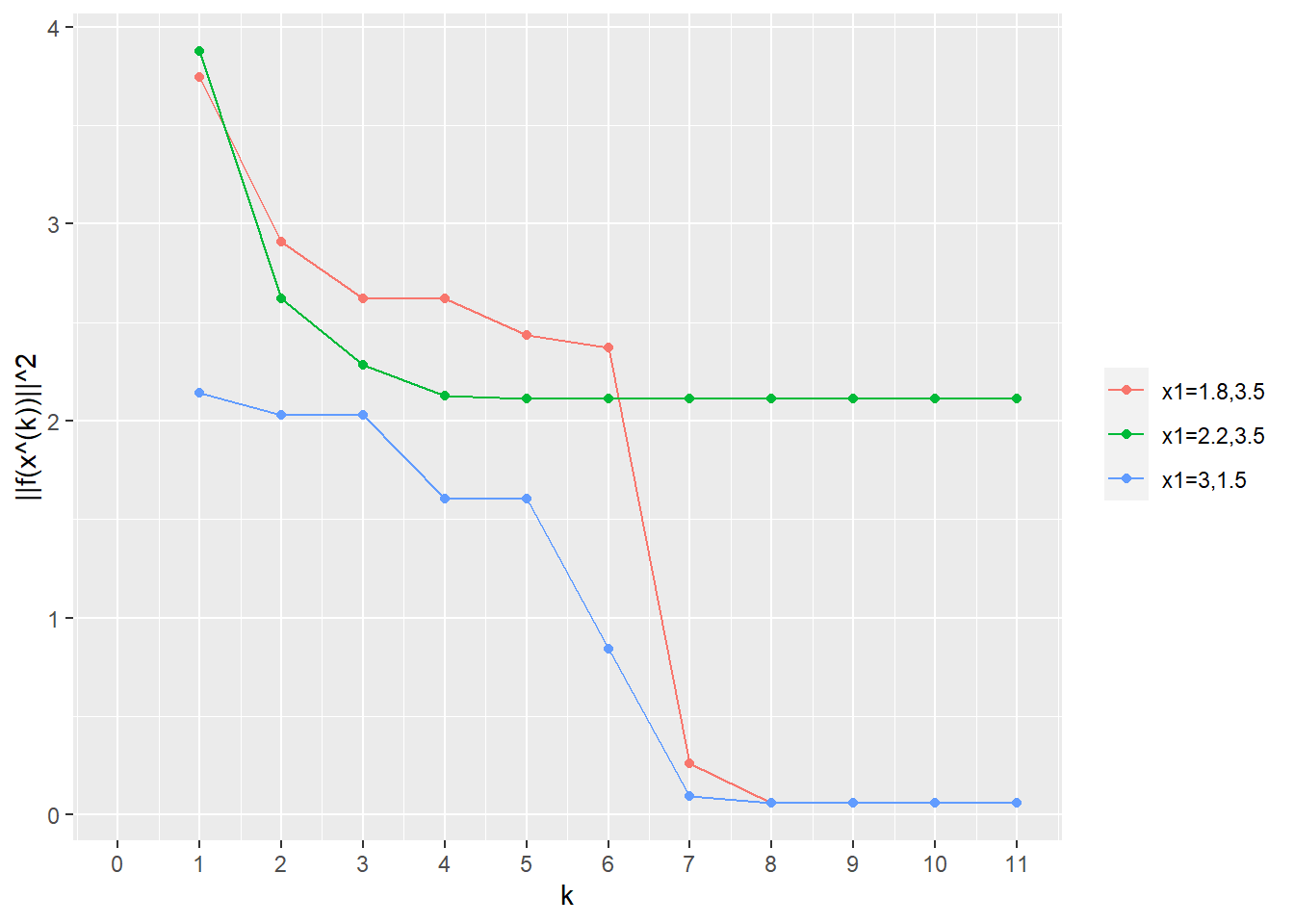
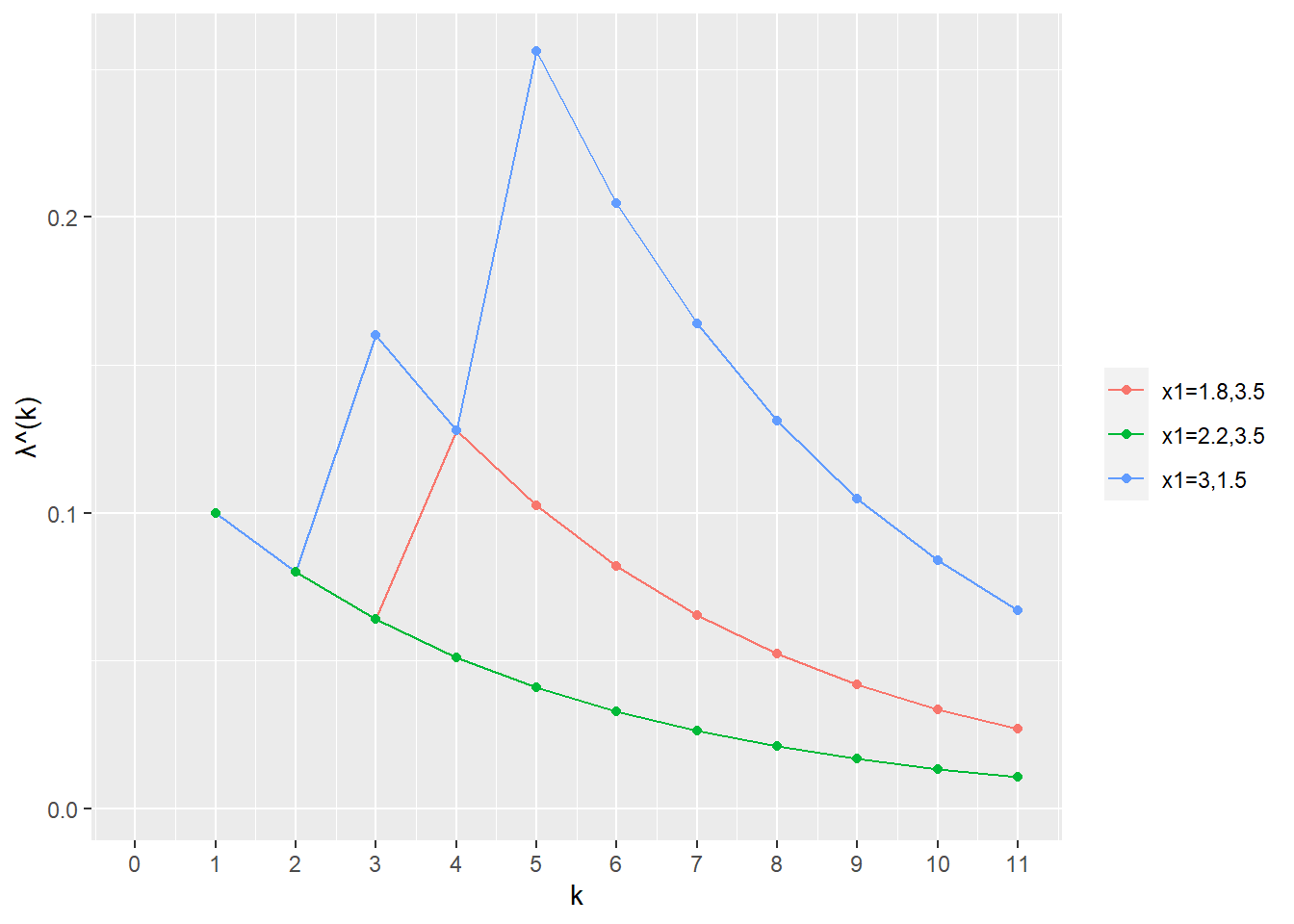
Simple example. (p.311)
\[\textbf{J}_1+\pmb{\lambda}\,\textbf{J}_2=\|\textbf{A}_1\textbf{x}-\textbf{b}_1\|^2+\pmb{\lambda}\|\textbf{A}_2\textbf{x}-\textbf{b}_2\|^2\]
# 各成分を正規分布に従う乱数とする、10行5列の係数行列Asを2つ作成。A1,A2。
As <- lapply(1:2, function(x) rnorm(n = 10 * 5) %>% matrix(nrow = 10))
As[[1]]
[,1] [,2] [,3] [,4] [,5]
[1,] -0.5764545 -1.2517794 -1.3194900 0.18314402 0.5819281
[2,] -0.3555892 -0.2350122 0.6910679 0.80742416 1.7557272
[3,] -0.2114378 0.2855546 -0.2730222 0.08816272 -0.1411785
[4,] -0.1265300 -1.0962285 -1.4525525 0.09323329 1.0301720
[5,] 0.3060832 -0.1173152 2.4873203 -0.81418482 0.4714445
[6,] -1.5783925 -0.8069189 -0.1399969 0.05974993 -0.8550522
[7,] 1.1555883 -1.8666035 -1.0254329 0.21135256 0.1310137
[8,] -0.3858997 -0.7980896 -1.9238427 -1.45321751 -0.2958475
[9,] -1.9126730 0.7222369 -1.5591818 0.86685282 -1.0525068
[10,] 0.3190208 0.4045224 -0.9810830 -2.47484050 -0.6824009
[[2]]
[,1] [,2] [,3] [,4] [,5]
[1,] -0.1192845080 0.09184665 -0.44677671 0.92305104 1.09375793
[2,] 0.0398167849 0.47012014 1.03793019 0.02403625 0.11670805
[3,] -0.0120158994 -0.41944969 -1.41912126 -0.03405822 -0.04802264
[4,] -0.5286360872 -0.47469296 -0.36026265 0.25609285 0.02248308
[5,] 1.8154152537 0.11621730 -0.81834900 -0.55309170 -1.66909138
[6,] -1.9669145494 -0.91310054 0.91149666 0.25743373 0.14615414
[7,] 0.0007931109 -1.27830980 0.01939041 1.61988551 1.12395816
[8,] 0.2012440621 0.78542964 -0.64569148 1.43332374 1.12957959
[9,] -0.2799596661 -0.36944560 0.36293862 -0.49902198 -2.61827575
[10,] -1.2678346877 -1.57077281 1.14957028 -1.15634153 -0.27903538# 各成分を正規分布に従う乱数とする、2行10列の目的変数行列bsを1つ作成。b1,b2。
bs <- rnorm(n = 2 * 10) %>% matrix(nrow = 2)
bs [,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0.9828555 0.08449577 1.0097209 0.25264180 -0.10292107 2.127883
[2,] -0.1374668 1.24323172 0.2357958 0.01651677 0.09162188 -1.200878
[,7] [,8] [,9] [,10]
[1,] -1.6337884 0.1521818 -1.1949303 0.9391474
[2,] 0.2111483 -0.2835552 0.8503887 -0.7893407# 係数ラムダ。200次元。
N <- 200
lambdas <- 10^seq(-4, 4, length.out = N)
head(lambdas)
tail(lambdas)[1] 0.0001000000 0.0001096986 0.0001203378 0.0001320088 0.0001448118
[6] 0.0001588565
[1] 6294.989 6905.514 7575.250 8309.942 9115.888 10000.000# 5行200列のゼロ行列xを1つ作成。
x <- matrix(0, 5, 200)
# ゼロベクトル(N次元)J1、j2を作成。
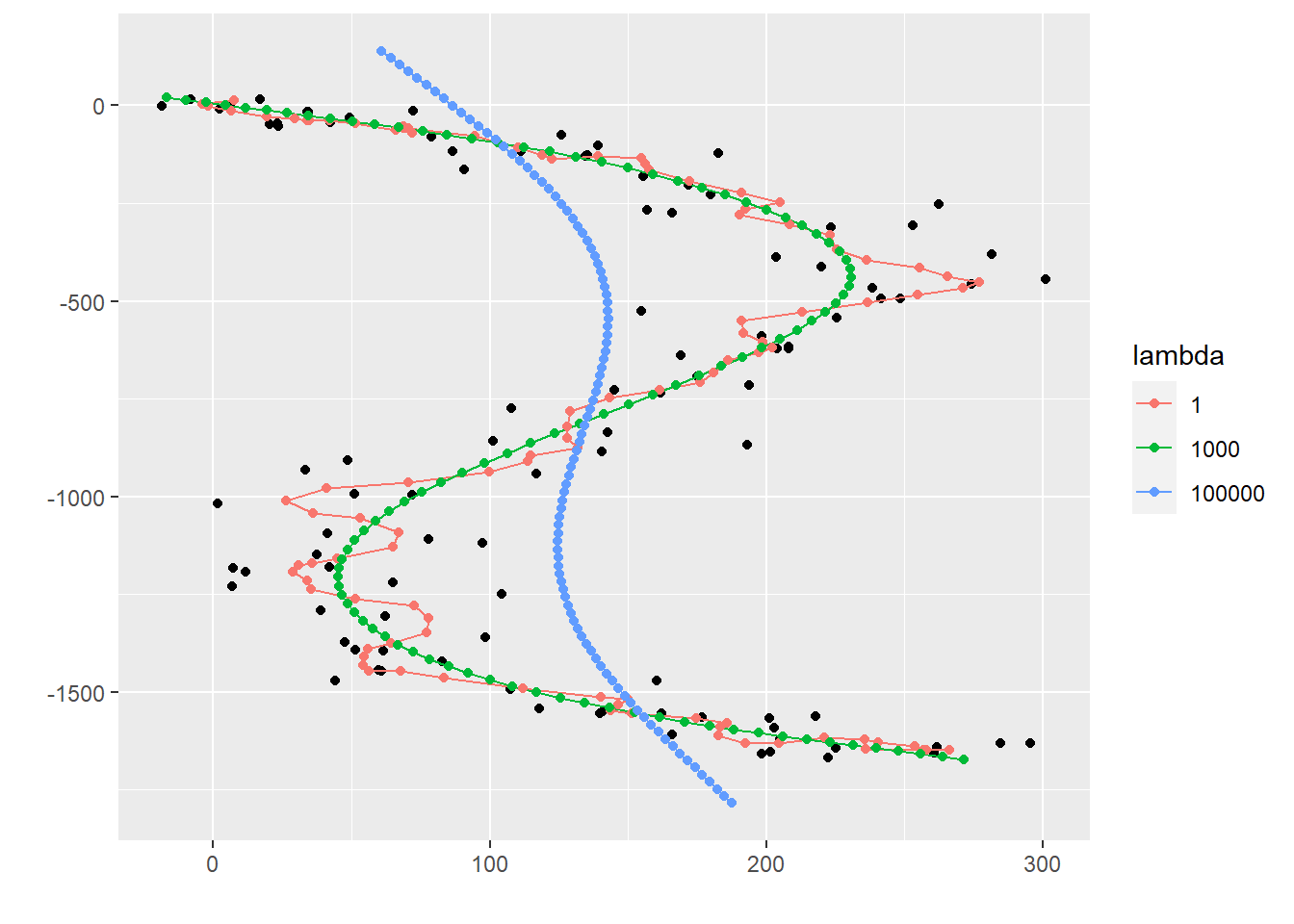
J1 <- J2 <- rep(0, N)func_mols_solve <- function(As, bs, lambdas) {
k <- length(lambdas)
# Atill 20(10*2)行5列の行列Atilを作成。
Atil <- lapply(seq(k), function(i) (lambdas[i]^0.5) * As[[i]]) %>% Reduce(function(x, y) rbind(x, y), .)
# btill 1行20列の行列btilを作成。
btil <- lapply(seq(k), function(i) (lambdas[i]^0.5) * bs[i, ]) %>% Reduce(function(x, y) c(x, y), .)
#
QR <- qr(x = Atil)
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
b <- t(Q) %*% btil
x_hat <- solve(a = R) %*% b
return(x_hat)
}
for (k in seq(N)) {
# xのk列目に推定量を代入
x[, k] <- func_mols_solve(As = As, bs = bs, lambdas = c(1, lambdas[k]))
J1[k] <- norm(As[[1]] %*% x[, k] - bs[1, ], type = "2")^2
J2[k] <- norm(As[[2]] %*% x[, k] - bs[2, ], type = "2")^2
}
x_t <- t(x)
colnames(x_t) <- c("y1", "y2", "y3", "y4", "y5")
df <- data.frame(lambdas, x_t) %>% gather(key = "key", value = "value", colnames(.)[-1])
# https://stackoverflow.com/questions/55113333/ggplot2-introduce-breaks-on-a-x-log-scale
x_breaks <- 10^pretty(log10(lambdas), n = 10)
x_labels <- formatC(x_breaks, format = "e", digits = 2)
g1 <- ggplot(data = df, mapping = aes(x = lambdas, y = value, color = key)) +
geom_line() +
scale_x_log10(breaks = x_breaks, labels = x_labels) +
theme(
axis.title.y = element_blank(), legend.title = element_blank(),
axis.text.x = element_text(angle = 90)
)df <- data.frame(lambdas, J1, J2) %>% gather(key = "key", value = "value", colnames(.)[-1])
g2 <- ggplot(data = df, mapping = aes(x = lambdas, y = value, color = key)) +
geom_line() +
scale_x_log10(breaks = x_breaks, labels = x_labels) +
theme(
axis.title.y = element_blank(), legend.title = element_blank(),
axis.text.x = element_text(angle = 90)
)QR <- qr(x = As[[1]])
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
b <- t(Q) %*% bs[1, ]
x1 <- solve(a = R) %*% b
#
QR <- qr(x = As[[2]])
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
b <- t(Q) %*% bs[2, ]
x2 <- solve(a = R) %*% b
#
J1p <- c(norm(As[[1]] %*% x1 - bs[1, ], type = "2")^2, norm(As[[1]] %*% x2 - bs[1, ], type = "2")^2)
J2p <- c(norm(As[[2]] %*% x1 - bs[2, ], type = "2")^2, norm(As[[2]] %*% x2 - bs[2, ], type = "2")^2)
#
g3 <- ggplot() +
geom_line(mapping = aes(x = J1, y = J2)) +
geom_point(mapping = aes(x = J1p, y = J2p))15 Multi-objective least squares > 15.3 Estimation and inversion > 15.3.2 Estimating a periodic time series (p.318)
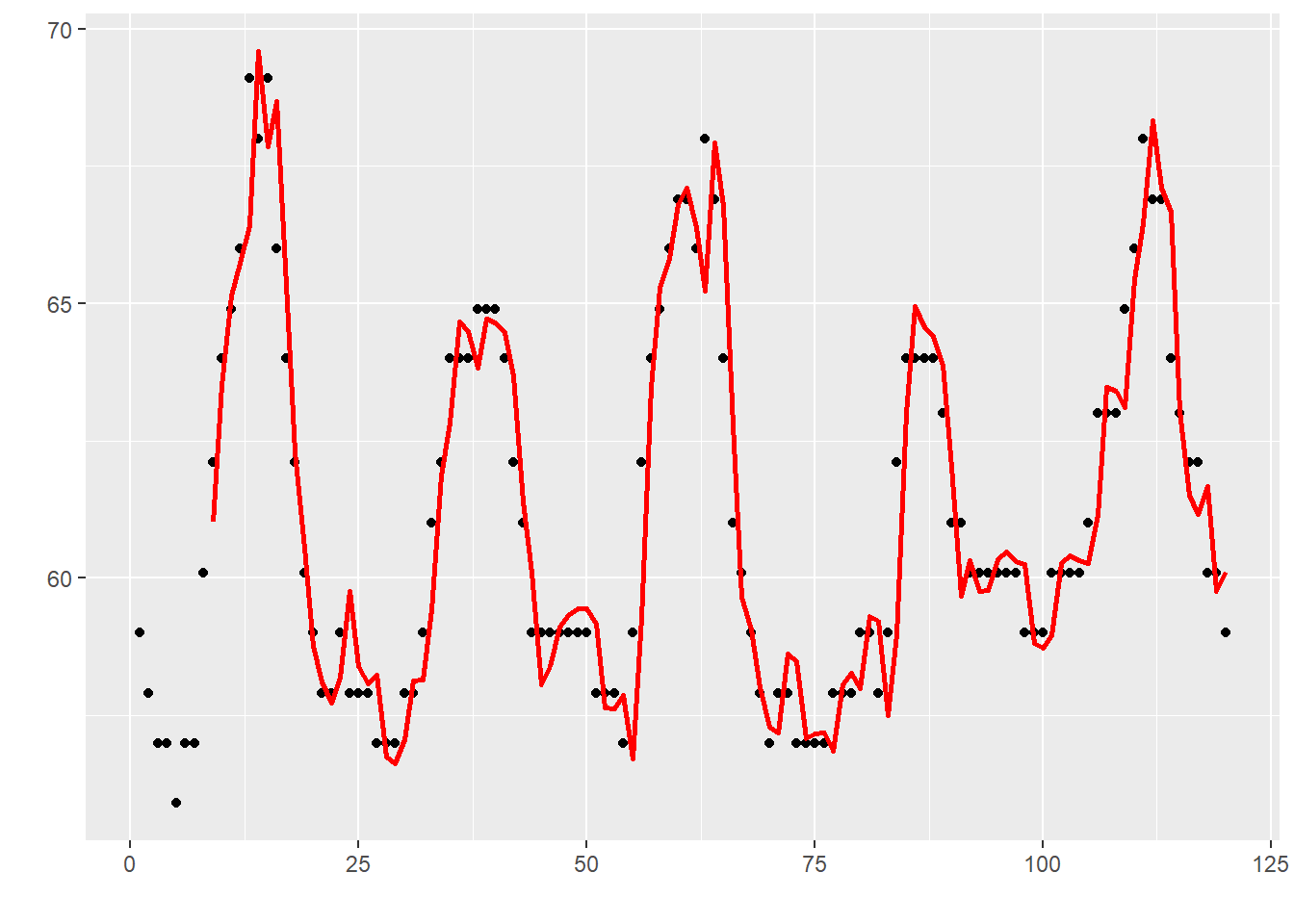
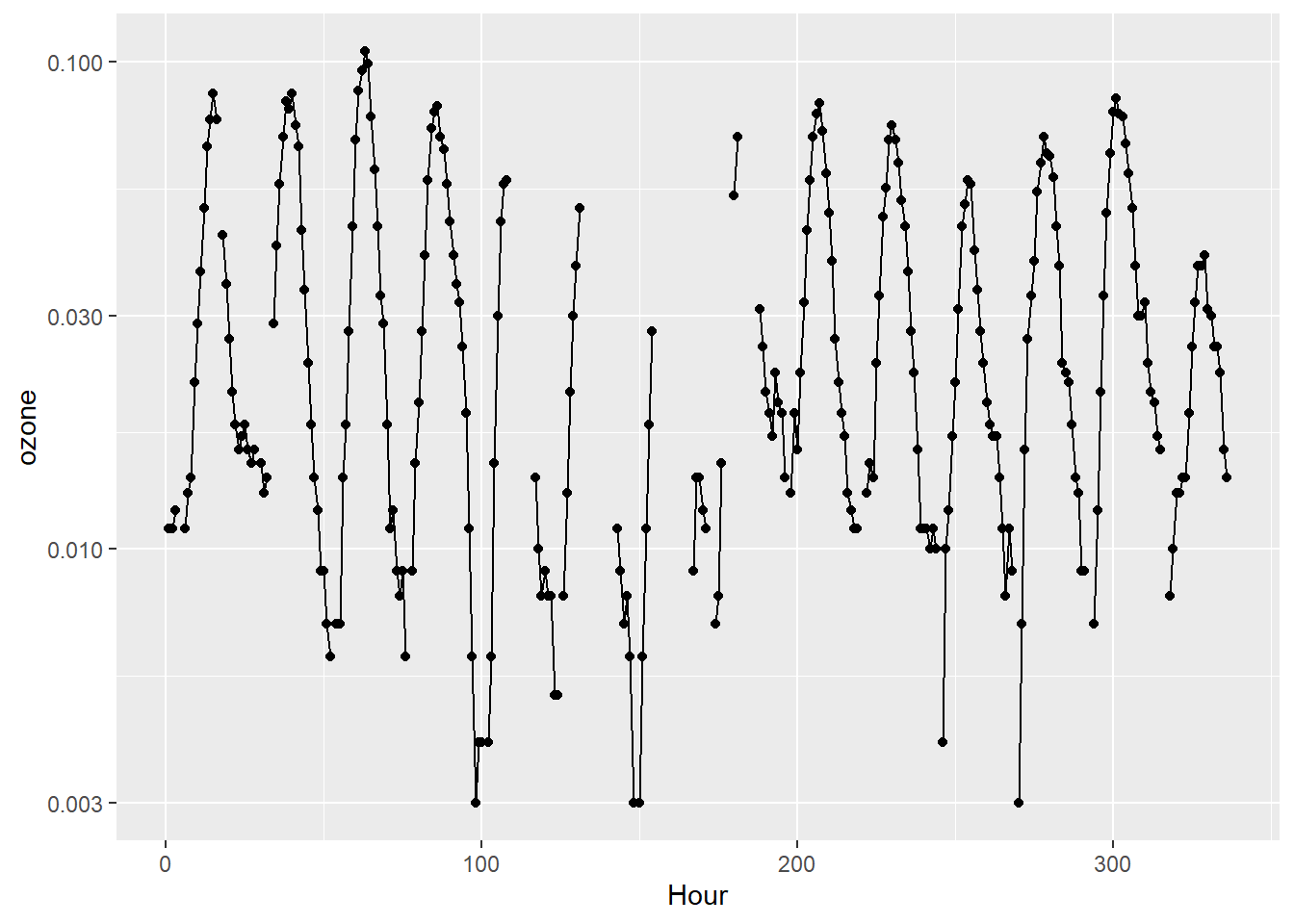
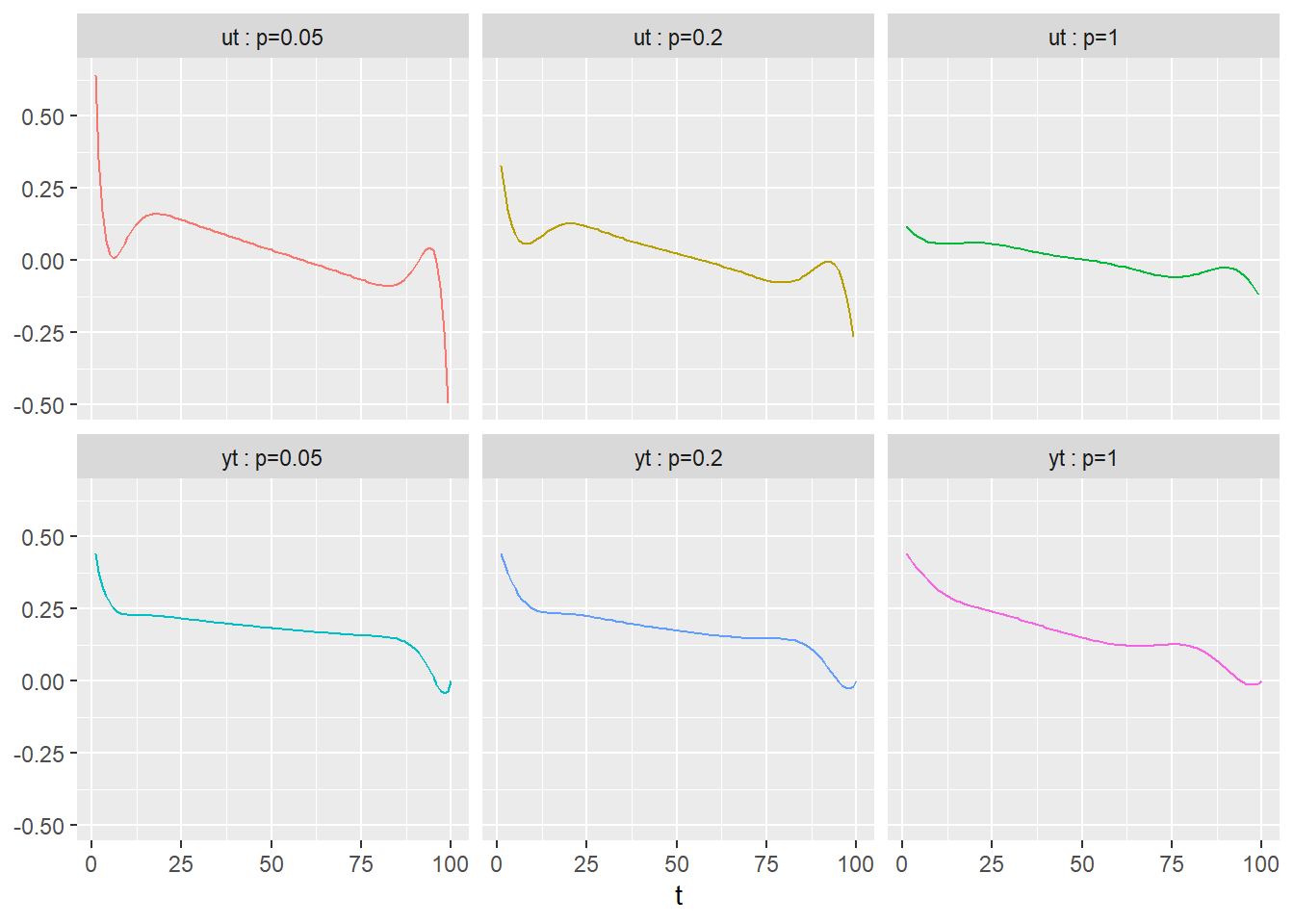
Example. (p.319)
# サンプルデータ
# カリフォルニア州アズサ 2014年6月最初の14日間の1時間毎オゾン量データ
summary(ozone)
length(ozone) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
0.00300 0.01200 0.02100 0.03046 0.04600 0.10500 61
[1] 336以下を最小にする。 \[\|\textbf{Ax}-\textbf{y}\|^2+\lambda\|\textbf{Dx}\|^2\]
library(ggplot2)
library(dplyr)
k <- 14
N <- k * 24
Hour <- seq(N)
g0 <- ggplot(mapping = aes(x = Hour, y = ozone)) +
geom_line() +
geom_point() +
scale_y_log10()
g0正規方程式 \[\textbf{x}=\left(\textbf{A}^{'}\textbf{A}\right)^{-1}\textbf{A}^{'}\textbf{b}\]
A <- lapply(seq(k), function(x) diag(1, 24)) %>% Reduce(function(x, y) rbind(x, y), .)
D <- diag(-1, 24) + rbind(cbind(rep(0, 23), diag(1, 23)), c(1, rep(0, 23)) %>% matrix(nrow = 1))
ind <-
{
!is.na(ozone)
} %>% which()
As <- list(A[ind, ], D)
bs <- list(log(ozone[ind]), rep(0, 24))
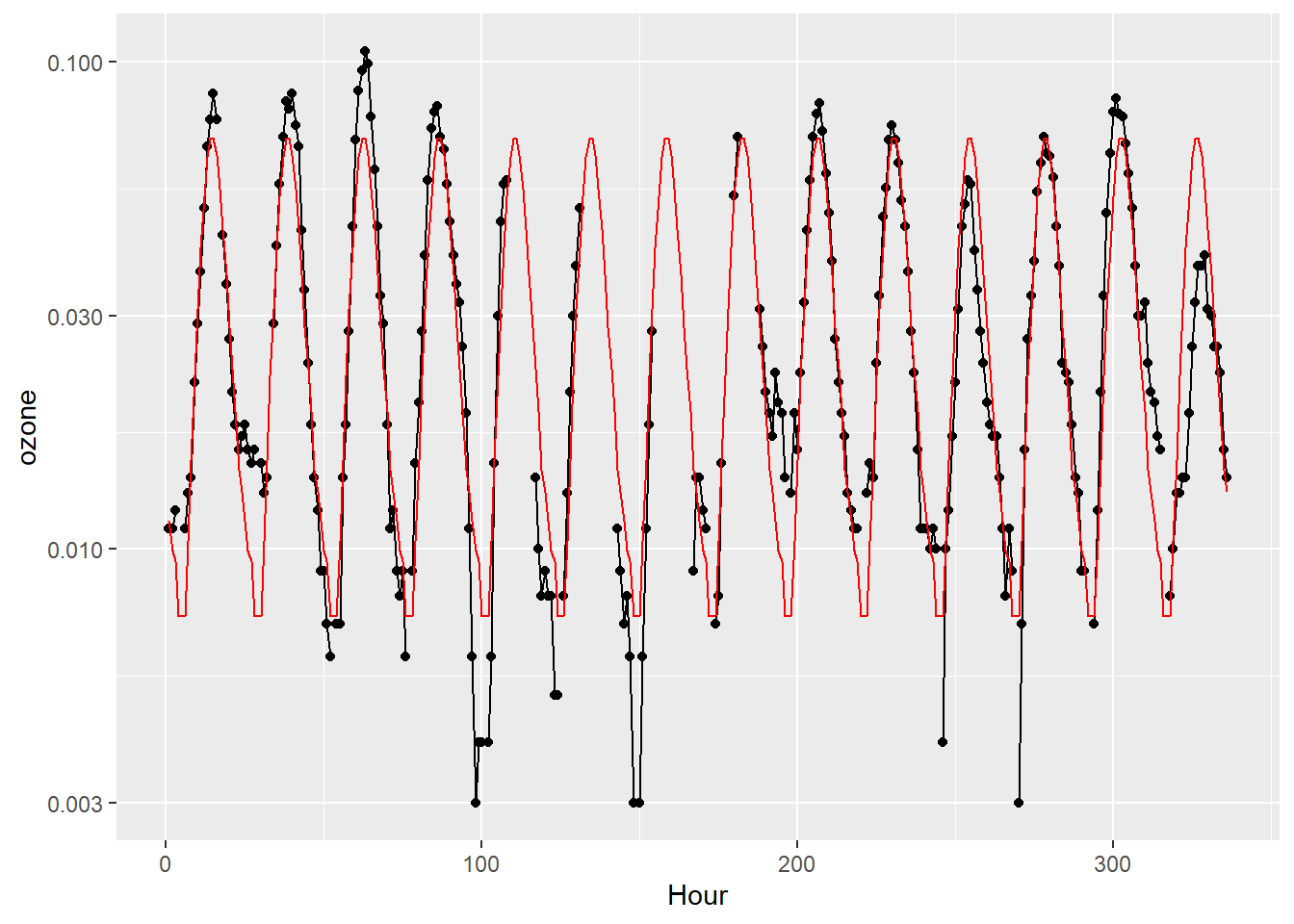
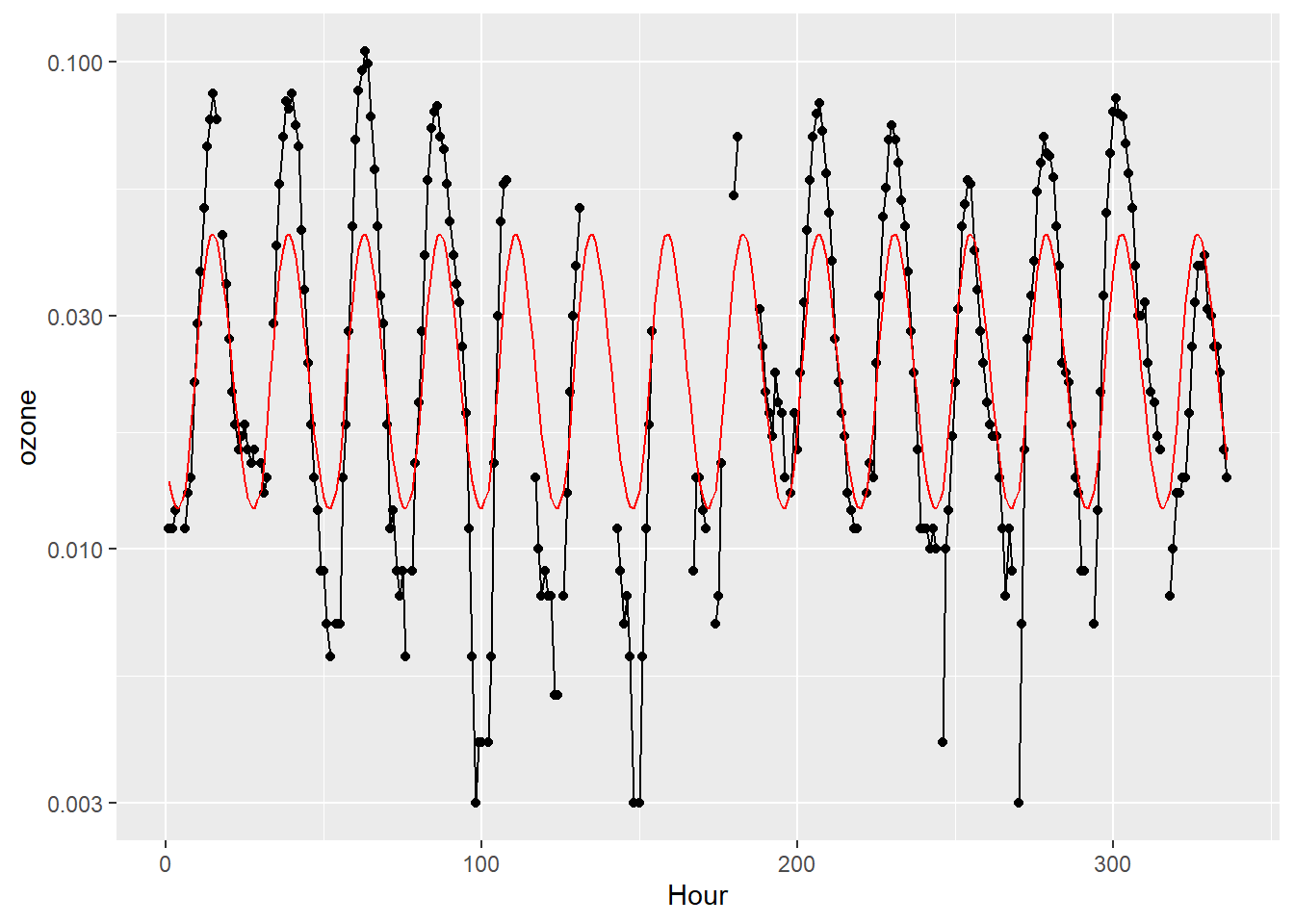
func_plot <- function(lambdas) {
n <- length(lambdas)
Atil <- lapply(seq(n), function(i) sqrt(lambdas[i]) * As[[i]]) %>% Reduce(function(x, y) rbind(x, y), .)
btil <- lapply(seq(n), function(i) sqrt(lambdas[i]) * bs[[i]]) %>% Reduce(function(x, y) c(x, y), .)
x <- {
{
t(Atil) %*% Atil
} %>% solve()
} %*% {
t(Atil) %*% btil
}
{
g0 + geom_line(mapping = aes(x = seq(N), y = rep(exp(x) %>% as.vector(), k)), color = "red")
} %>% print()
}
list(
head_A = head(A) %>% data.frame(), tail_A = tail(A) %>% data.frame(),
head_D = head(D) %>% data.frame(), tail_D = tail(D) %>% data.frame(), dim_A = dim(A), dim_D = dim(D)
)$head_A
X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11 X12 X13 X14 X15 X16 X17 X18 X19 X20 X21
1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
2 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
3 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
4 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
5 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
6 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
X22 X23 X24
1 0 0 0
2 0 0 0
3 0 0 0
4 0 0 0
5 0 0 0
6 0 0 0
$tail_A
X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11 X12 X13 X14 X15 X16 X17 X18 X19 X20
[331,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
[332,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
[333,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
[334,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
[335,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
[336,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
X21 X22 X23 X24
[331,] 0 0 0 0
[332,] 0 0 0 0
[333,] 1 0 0 0
[334,] 0 1 0 0
[335,] 0 0 1 0
[336,] 0 0 0 1
$head_D
X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11 X12 X13 X14 X15 X16 X17 X18 X19 X20 X21
1 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
2 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
3 0 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
4 0 0 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
5 0 0 0 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
6 0 0 0 0 0 -1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
X22 X23 X24
1 0 0 0
2 0 0 0
3 0 0 0
4 0 0 0
5 0 0 0
6 0 0 0
$tail_D
X1 X2 X3 X4 X5 X6 X7 X8 X9 X10 X11 X12 X13 X14 X15 X16 X17 X18 X19 X20
[19,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1 1
[20,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1
[21,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
[22,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
[23,] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
[24,] 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
X21 X22 X23 X24
[19,] 0 0 0 0
[20,] 1 0 0 0
[21,] -1 1 0 0
[22,] 0 -1 1 0
[23,] 0 0 -1 1
[24,] 0 0 0 -1
$dim_A
[1] 336 24
$dim_D
[1] 24 2415 Multi-objective least squares > 15.4 Regularized data fitting (p.325)
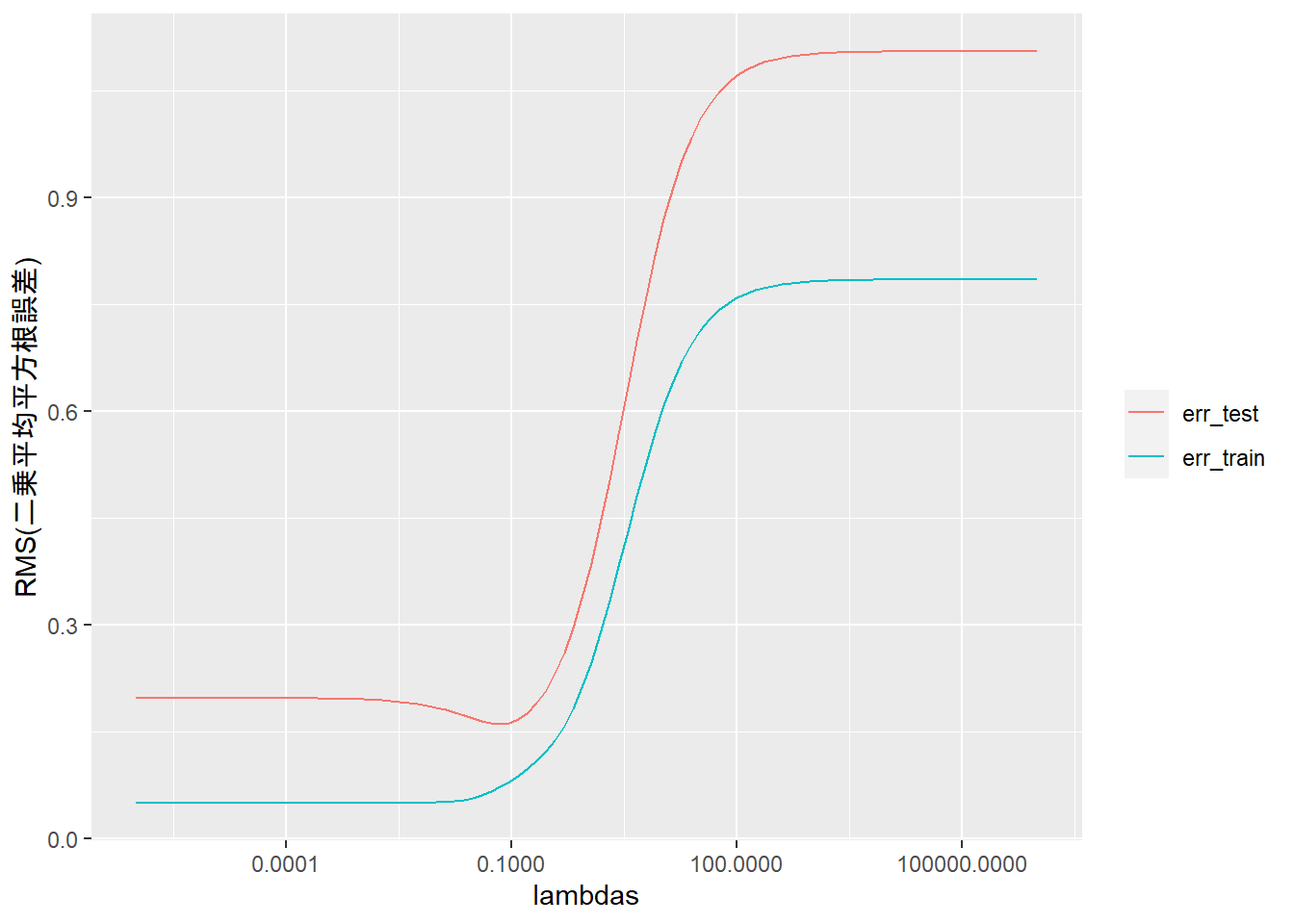
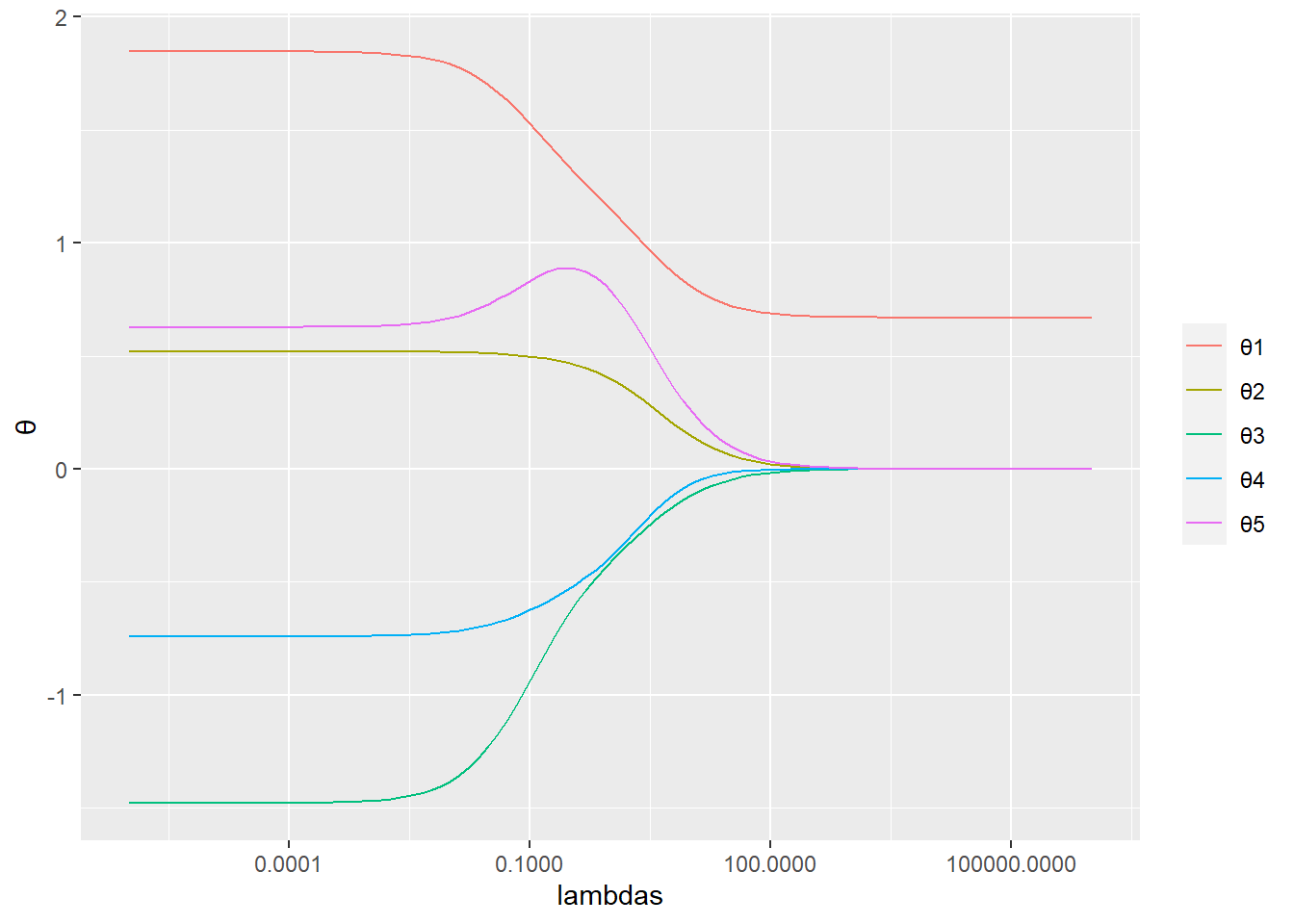
Example. (p.329)
モデルは以下の通り。 \[\hat{f}(x)=\displaystyle\sum_{k=1}^5\theta_k\,f_k(x)\] ここで、\[f_1(x)=1,\quad f_{k+1}(x)=\textrm{sin}(\omega_k\,x+\phi_k)\]
以下を最小にする。 \[\displaystyle\sum_{i=1}^N\left(y^{(i)}-\displaystyle\sum_{k=1}^5\theta_k\,f_k\left(x^{(i)}\right)\right)^2+\lambda\displaystyle\sum_{k=2}^5\theta_k^2\]
# サンプルデータ
xtrain <-
c(0.10683, 0.25578, 0.27112, 0.30299, 0.50204, 0.65845, 0.68423, 0.70259, 0.73406, 0.94035)
ytrain <-
c(1.82422, 0.813549, 0.92406, 0.42067, 0.446178, -0.0373407, -0.210935, -0.103327, 0.332097, 2.29278)
xtest <-
c(
0.396674, 0.777517, 0.1184, 0.223266, 0.901463, 0.358033, 0.260402, 0.804281, 0.631664, 0.149704,
0.551333, 0.663999, 0.164948, 0.651698, 0.123026, 0.337066, 0.083208, 0.204422, 0.978, 0.403676
)
ytest <-
c(
-1.05772, 0.879117, 1.98136, 0.867012, 2.1365, -0.701948, 0.941469, 1.49755, 0.550205, 1.34245,
1.21445, 0.00449111, 0.957535, 0.077864, 1.73558, -0.325244, 2.56555, 1.10081, 2.70644, -1.10049
)
sapply(list(xtrain, ytrain, xtest, ytest), function(x) length(x))[1] 10 10 20 20library(tensor)
N <- length(ytrain)
Ntest <- length(ytest)
p <- 5
# 本例では ω と Φ は以下の通りに設定。
omega <- c(13.69, 3.55, 23.25, 6.03)
phi <- c(0.21, 0.02, -1.87, 1.72)
A <- cbind(rep(1, N), {
tensor(xtrain, omega) + tensor(rep(1, N), phi)
} %>% sin())
Atest <- cbind(rep(1, Ntest), {
tensor(xtest, omega) + tensor(rep(1, Ntest), phi)
} %>% sin())
npts <- 100
lambdas <- 10^(seq(-6, 6, length.out = npts))
err_train <- rep(0, npts)
err_test <- rep(0, npts)
thetas <- matrix(0, nrow = p, ncol = npts)
As <- bs <- list()
As[[1]] <- A
As[[2]] <- cbind(rep(0, p - 1), diag(1, p - 1))
bs[[1]] <- ytrain
bs[[2]] <- rep(0, p - 1)
list(As = As, bs = bs)$As
$As[[1]]
[,1] [,2] [,3] [,4] [,5]
[1,] 1 0.9948324 0.3887242 0.5759759 0.7014342
[2,] 1 -0.5396620 0.8004341 -0.8047726 -0.1204674
[3,] 1 -0.7033080 0.8318740 -0.9613729 -0.2116481
[4,] 1 -0.9378355 0.8892096 -0.8951055 -0.3944204
[5,] 1 0.7171765 0.9733358 -0.3687390 -0.9993906
[6,] 1 0.1992548 0.7061848 0.7659977 -0.5586289
[7,] 1 -0.1517423 0.6385219 0.9951213 -0.4234755
[8,] 1 -0.3928044 0.5870404 0.9466722 -0.3207939
[9,] 1 -0.7409631 0.4931262 0.4891093 -0.1363772
[10,] 1 0.4942926 -0.2149590 0.9101233 0.8944167
$As[[2]]
[,1] [,2] [,3] [,4] [,5]
[1,] 0 1 0 0 0
[2,] 0 0 1 0 0
[3,] 0 0 0 1 0
[4,] 0 0 0 0 1
$bs
$bs[[1]]
[1] 1.8242200 0.8135490 0.9240600 0.4206700 0.4461780 -0.0373407
[7] -0.2109350 -0.1033270 0.3320970 2.2927800
$bs[[2]]
[1] 0 0 0 0for (k in seq(npts)) {
lam <- c(1, lambdas[k])
n <- length(lam)
Atil <- lapply(seq(n), function(i) sqrt(lam[i]) * As[[i]]) %>% Reduce(function(x, y) rbind(x, y), .)
btil <- lapply(seq(n), function(i) sqrt(lam[i]) * bs[[i]]) %>% Reduce(function(x, y) c(x, y), .)
# 正規方程式
theta <- solve(t(Atil) %*% Atil) %*% (t(Atil) %*% btil)
err_train[k] <- (sum((ytrain - A %*% theta)^2) / length(ytrain))^0.5
err_test[k] <- (sum((ytest - Atest %*% theta)^2) / length(ytest))^0.5
thetas[, k] <- theta
}
data.frame(lambdas, err_train, err_test) %>%
gather(key = "key", value = "value", colnames(.)[-1]) %>%
ggplot(mapping = aes(x = lambdas, y = value, color = key)) +
geom_line() +
scale_x_log10() +
labs(y = "RMS(二乗平均平方根誤差)") +
theme(legend.title = element_blank())16 Constrained least squares > 16.1 Constrained least squares problem (p.339)
Example. (p.340)
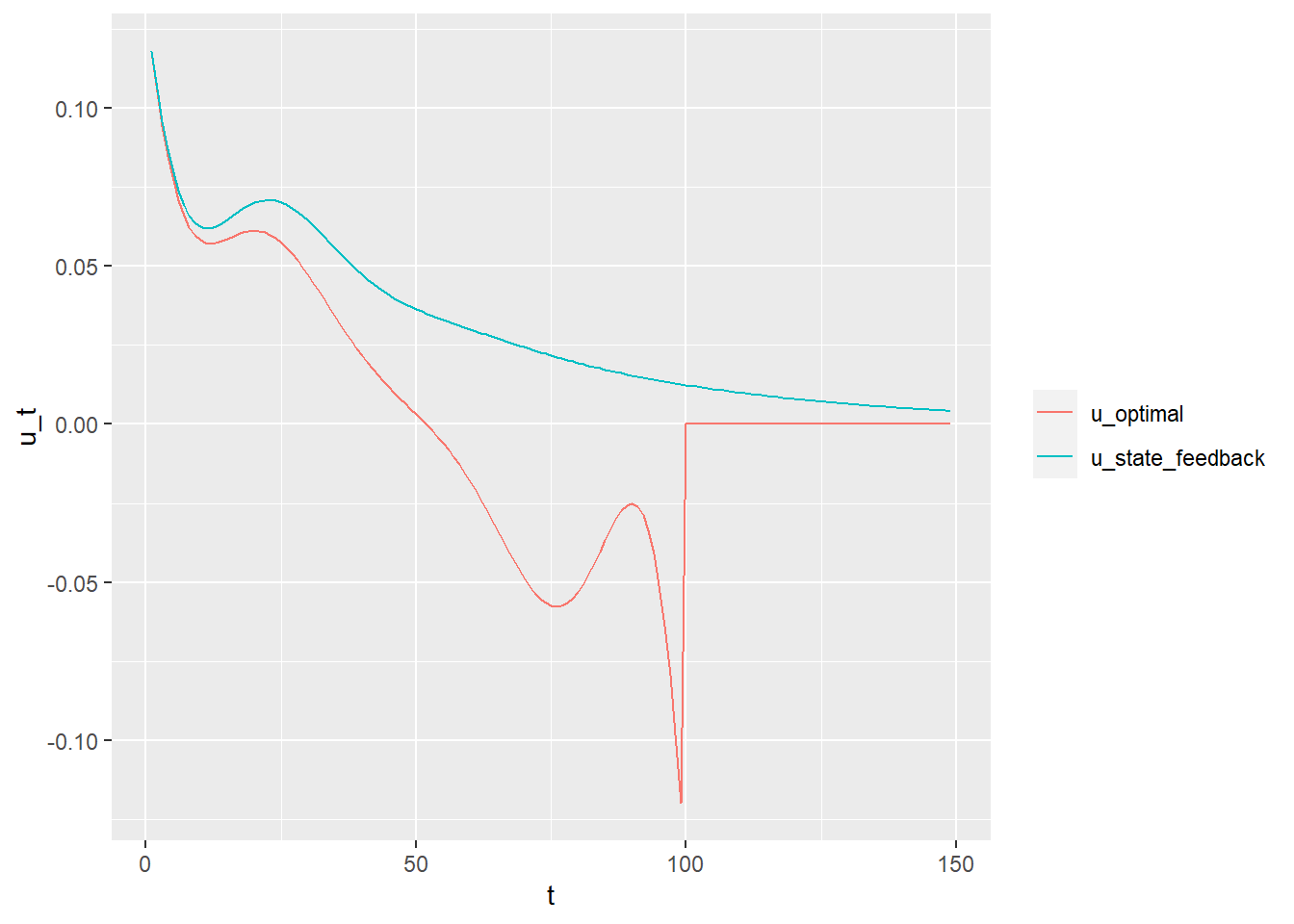
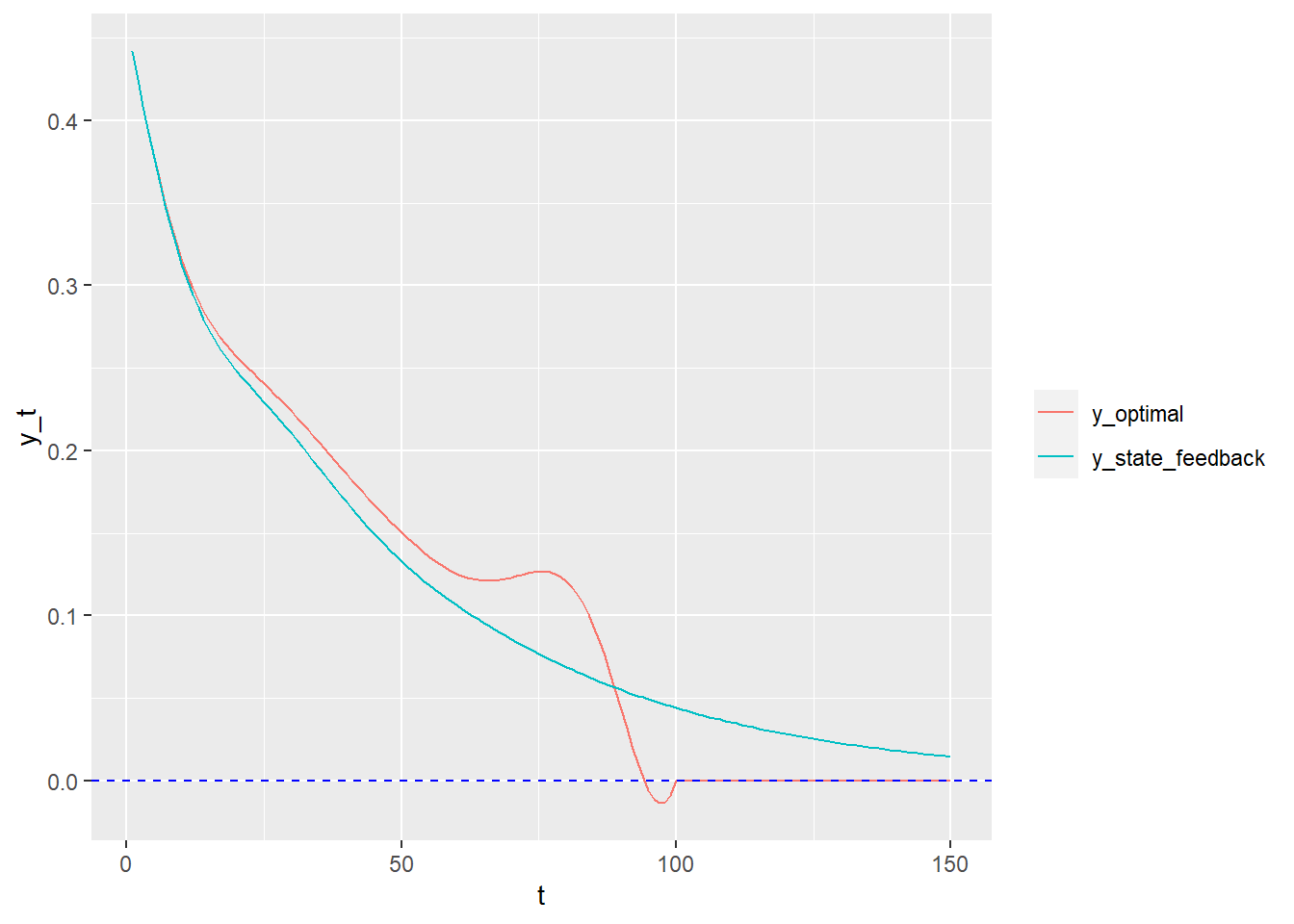
\(\textbf{Cx}=\textbf{d}\)を制約条件とした上で\[\|\textbf{Ax}-\textbf{b}\|^2+\lambda\|\textbf{Cx}-\textbf{d}\|^2\]を最小にする\(\hat{\textbf{x}}\)を求める。
M <- 70
N <- 2 * M
xleft <- runif(n = M) - 1 # 左半分 <= 0
xright <- runif(n = M) # 右半分 > 0
x <- c(xleft, xright)
y <- x^3 - x + 0.4 / (1 + 25 * (x^2)) + 0.05 * rnorm(n = N)
n <- 4 # (n-1)次多項式回帰
vandermonde_matrix_l <- outer(X = xleft, Y = seq(n) - 1, FUN = "^")
vandermonde_matrix_r <- outer(X = xright, Y = seq(n) - 1, FUN = "^")
A <- rbind(cbind(vandermonde_matrix_l, matrix(0, M, n)), cbind(matrix(0, M, n), vandermonde_matrix_r))
b <- y
# 制約条件
C <- rbind(c(1, rep(0, n - 1), -1, rep(0, n - 1)), c(0, 1, rep(0, n - 2), 0, -1, rep(0, n - 2)))
d <- rep(0, 2) # p(a)=q(a) かつ p'(a)=q'(a)
list(A_head = head(A), A_tail = tail(A), b_head = head(b), b_tail = tail(b), C = C, d = d)$A_head
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,] 1 -0.22584533 0.051006113 -0.0115194923 0 0 0 0
[2,] 1 -0.93850066 0.880783494 -0.8266158924 0 0 0 0
[3,] 1 -0.82990560 0.688743308 -0.5715919297 0 0 0 0
[4,] 1 -0.12982116 0.016853534 -0.0021879453 0 0 0 0
[5,] 1 -0.07648605 0.005850116 -0.0004474523 0 0 0 0
[6,] 1 -0.83134750 0.691138662 -0.5745763970 0 0 0 0
$A_tail
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[135,] 0 0 0 0 1 0.08709203 0.007585021 0.0006605948
[136,] 0 0 0 0 1 0.71907624 0.517070641 0.3718132130
[137,] 0 0 0 0 1 0.74376411 0.553185047 0.4114391830
[138,] 0 0 0 0 1 0.93150453 0.867700695 0.8082671305
[139,] 0 0 0 0 1 0.16058614 0.025787909 0.0041411809
[140,] 0 0 0 0 1 0.33064966 0.109329197 0.0361496619
$b_head
[1] 0.48326432 0.06828323 0.32857088 0.38150143 0.45600392 0.30391248
$b_tail
[1] 0.19722631 -0.29644311 -0.31285371 -0.07743325 0.10955205 -0.15481355
$C
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,] 1 0 0 0 -1 0 0 0
[2,] 0 1 0 0 0 -1 0 0
$d
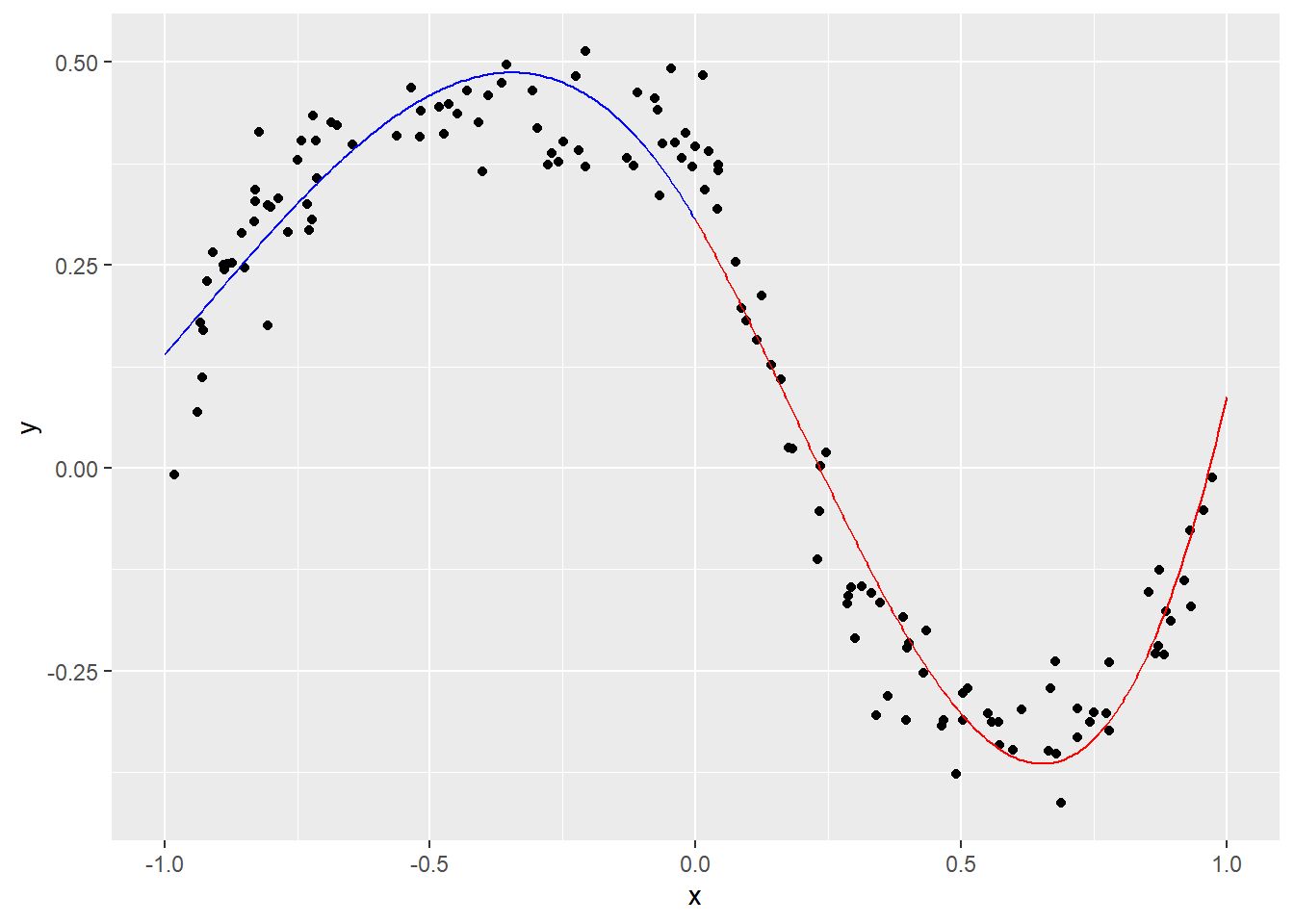
[1] 0 0\(\hat{f}(x)\)は\(x=a\)を境に以下の2式からなる(本例では\(a=0\))。
\[\begin{aligned}p(x|x\leq a)=\theta_1+\theta_2x+\theta_3x^2+\theta_4x^3\\ q(x|x>a)=\theta_5+\theta_6x+\theta_7x^2+\theta_8x^3\end{aligned}\]
よって誤差自乗平方和は、
\[\displaystyle\sum_{i=1}^M\left(\theta_1+\theta_2x_i+\theta_3x_i^2+\theta_4x_i^3-y_i\right)^2+\displaystyle\sum_{i=M+1}^N\left(\theta_5+\theta_6x_i+\theta_7x_i^2+\theta_8x_i^3-y_i\right)^2\]であり、連続データであるため\[p(x=a)-q(x=a)=0\]かつ\[p^{'}(x=a)-q^{'}(x=a)=0\]から\[p(a)-q(a)=0\,\therefore \theta_1+\theta_2a+\theta_3a^2+\theta_4a^3-\theta_5-\theta_6a-\theta_7a^2-\theta_8a^3=0\]および\[p^{'}(x=a)-q^{'}(x=a)=0\,\therefore \theta_2+2\theta_3a+3\theta_4a^2-\theta_6-2\theta_7a-3\theta_8a^2=0\]を満たす必要があり(スプライン)、行列で表すと\[C\theta=\begin{bmatrix}1&a&a^2&a^3&-1&-a&-a^2&-a^3\\0&1&2a&3a^2&0&-1&-2a&-3a^2\end{bmatrix}\theta=\begin{bmatrix}0\\0\end{bmatrix}\]
# step1
QR <- qr(x = rbind(A, C))
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
Q1 <- head(Q, nrow(A))
Q2 <- tail(Q, -nrow(A))
# step2
QR <- qr(x = t(Q2))
Qtil <- qr.Q(qr = QR)
Rtil <- qr.R(qr = QR)
# step3
QR <- qr(x = t(Rtil))
Q0 <- qr.Q(qr = QR)
R0 <- qr.R(qr = QR)
b0 <- t(Q0) %*% d
x_hat <- solve(a = R0) %*% b0
# step4
QR <- qr(x = Rtil)
Q0 <- qr.Q(qr = QR)
R0 <- qr.R(qr = QR)
b0 <- t(Q0) %*% ({
(2 * t(Qtil)) %*% (t(Q1) %*% b)
} - 2 * x_hat)
x_hat <- solve(a = R0) %*% b0
w <- x_hat
# step5
QR <- qr(x = R)
Q0 <- qr.Q(qr = QR)
R0 <- qr.R(qr = QR)
b0 <- t(Q0) %*% {{
t(Q1) %*% b
} - {
t(Q2) %*% (w / 2)
}}
theta <- solve(a = R0) %*% b0
theta [,1]
[1,] 0.3055131
[2,] -1.1355761
[3,] -2.0067202
[4,] -0.7055567
[5,] 0.3055131
[6,] -1.1355761
[7,] -1.2440561
[8,] 2.1613579Npl <- 200
#
xpl_left <- seq(-1, 0, length.out = Npl)
ypl_left <- outer(X = xpl_left, Y = seq(n) - 1, FUN = "^") %*% head(theta, n)
#
xpl_right <- seq(0, 1, length.out = Npl)
ypl_right <- outer(X = xpl_right, Y = seq(n) - 1, FUN = "^") %*% tail(theta, -n)
#
ggplot() +
geom_point(mapping = aes(x = x, y = y)) +
geom_line(mapping = aes(x = xpl_left, y = ypl_left), color = "blue") +
geom_line(mapping = aes(x = xpl_right, y = ypl_right), color = "red")Advertising budget allocation. (p.341)
n <- 3 # チャンネル数
m <- 10 # 属性数
R <- c( # 1ドル当たり視聴数(単位:1000views)
0.97, 1.86, 0.41,
1.23, 2.18, 0.53,
0.80, 1.24, 0.62,
1.29, 0.98, 0.51,
1.10, 1.23, 0.69,
0.67, 0.34, 0.54,
0.87, 0.26, 0.62,
1.10, 0.16, 0.48,
1.92, 0.22, 0.71,
1.29, 0.12, 0.62
) %>% matrix(ncol = 3, byrow = T)
# s:広告支出
# v^des:目標視聴数
B <- 1284以下を最小にする。 \[\|Rs-v^{\textrm{des}}\|^2\]
但し制約として広告総予算を\(B\)とする。
\[\textbf{1}^{'}s=B\]
なお本例では\(B=1284\)とする。
A <- R
b <- rep(10^3, m) # 百万視聴/チャンネル
C <- rep(1, n)
d <- B# step1
QR <- qr(x = rbind(A, C))
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
Q1 <- head(Q, nrow(A))
Q2 <- tail(Q, -nrow(A))
# step2
QR <- qr(x = t(Q2))
Qtil <- qr.Q(qr = QR)
Rtil <- qr.R(qr = QR)
# step3
QR <- qr(x = t(Rtil))
Q0 <- qr.Q(qr = QR)
R0 <- qr.R(qr = QR)
b0 <- t(Q0) %*% d
x_hat <- solve(a = R0) %*% b0
# step4
QR <- qr(x = Rtil)
Q0 <- qr.Q(qr = QR)
R0 <- qr.R(qr = QR)
b0 <- t(Q0) %*% ({
(2 * t(Qtil)) %*% (t(Q1) %*% b)
} - 2 * x_hat)
x_hat <- solve(a = R0) %*% b0
w <- x_hat
# step5
QR <- qr(x = R)
Q0 <- qr.Q(qr = QR)
R0 <- qr.R(qr = QR)
b0 <- t(Q0) %*% {{
t(Q1) %*% b
} - {
t(Q2) %*% (w / 2)
}}
theta <- solve(a = R0) %*% b0
theta [,1]
[1,] 315.1682
[2,] 109.8664
[3,] 858.9654result <- A %*% theta %>%
data.frame() %>%
{
tmp <- add_column(.data = ., Group = paste0("Group ", seq(nrow(.))), .before = 1)
tmp
} %>%
{
colnames(.)[2] <- "Impressions"
.
}
result$Group <- factor(result$Group, levels = result$Group)
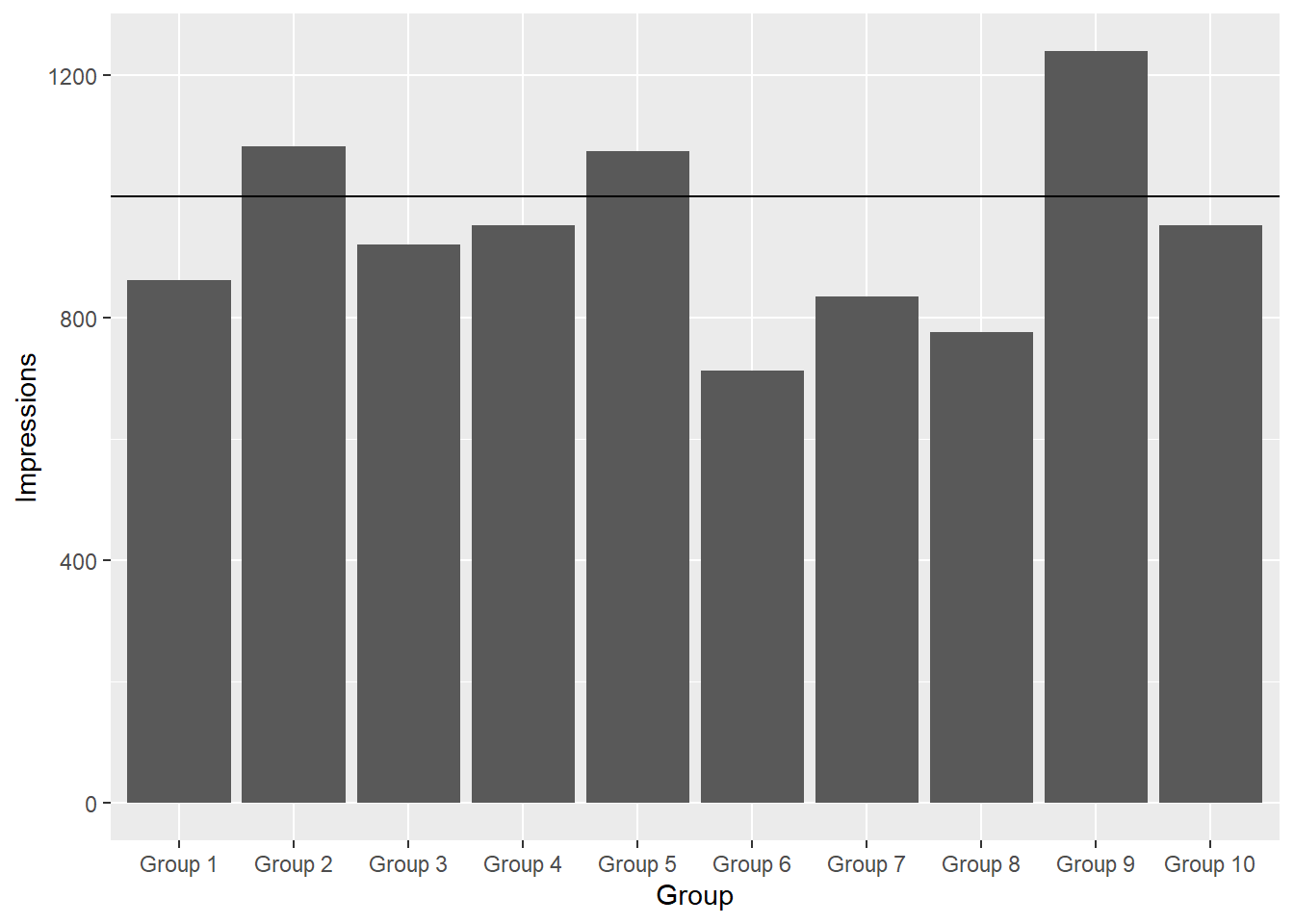
ggplot(data = result) +
geom_bar(mapping = aes(x = Group, y = Impressions), stat = "identity", ) +
geom_hline(yintercept = 1000)
result Group Impressions
1 Group 1 862.2405
2 Group 2 1082.4173
3 Group 3 920.9275
4 Group 4 952.3084
5 Group 5 1074.5068
6 Group 6 712.3586
7 Group 7 835.3201
8 Group 8 776.5670
9 Group 9 1239.1590
10 Group 10 952.309516 Constrained least squares > 16.1 Constrained least squares problem > 16.1.1 Least norm problem (p.342)
Example. (p.343)
最小ノルム問題は、\[\textbf{Cx}=\textbf{d}\]の制約を満たし、\[\|\textbf{Ax}-\textbf{b}\|^2=\|\textbf{Ix}-\textbf{0}\|^2=\|\textbf{x}\|^2\]が最小となる\(\hat{x}\)を求める問題。
A <- diag(1, nrow = 10, ncol = 10)
b <- rep(0, 10)
C <- rbind(rep(1, 10), seq(9.5, 0.4, -1))
d <- c(0, 1)# step1
QR <- qr(x = rbind(A, C))
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
Q1 <- head(Q, nrow(A))
Q2 <- tail(Q, -nrow(A))
# step2
QR <- qr(x = t(Q2))
Qtil <- qr.Q(qr = QR)
Rtil <- qr.R(qr = QR)
# step3
QR <- qr(x = t(Rtil))
Q0 <- qr.Q(qr = QR)
R0 <- qr.R(qr = QR)
b0 <- t(Q0) %*% d
x_hat <- solve(a = R0) %*% b0
# step4
QR <- qr(x = Rtil)
Q0 <- qr.Q(qr = QR)
R0 <- qr.R(qr = QR)
b0 <- t(Q0) %*% ({
(2 * t(Qtil)) %*% (t(Q1) %*% b)
} - 2 * x_hat)
x_hat <- solve(a = R0) %*% b0
w <- x_hat
# step5
QR <- qr(x = R)
Q0 <- qr.Q(qr = QR)
R0 <- qr.R(qr = QR)
b0 <- t(Q0) %*% {{
t(Q1) %*% b
} - {
t(Q2) %*% (w / 2)
}}
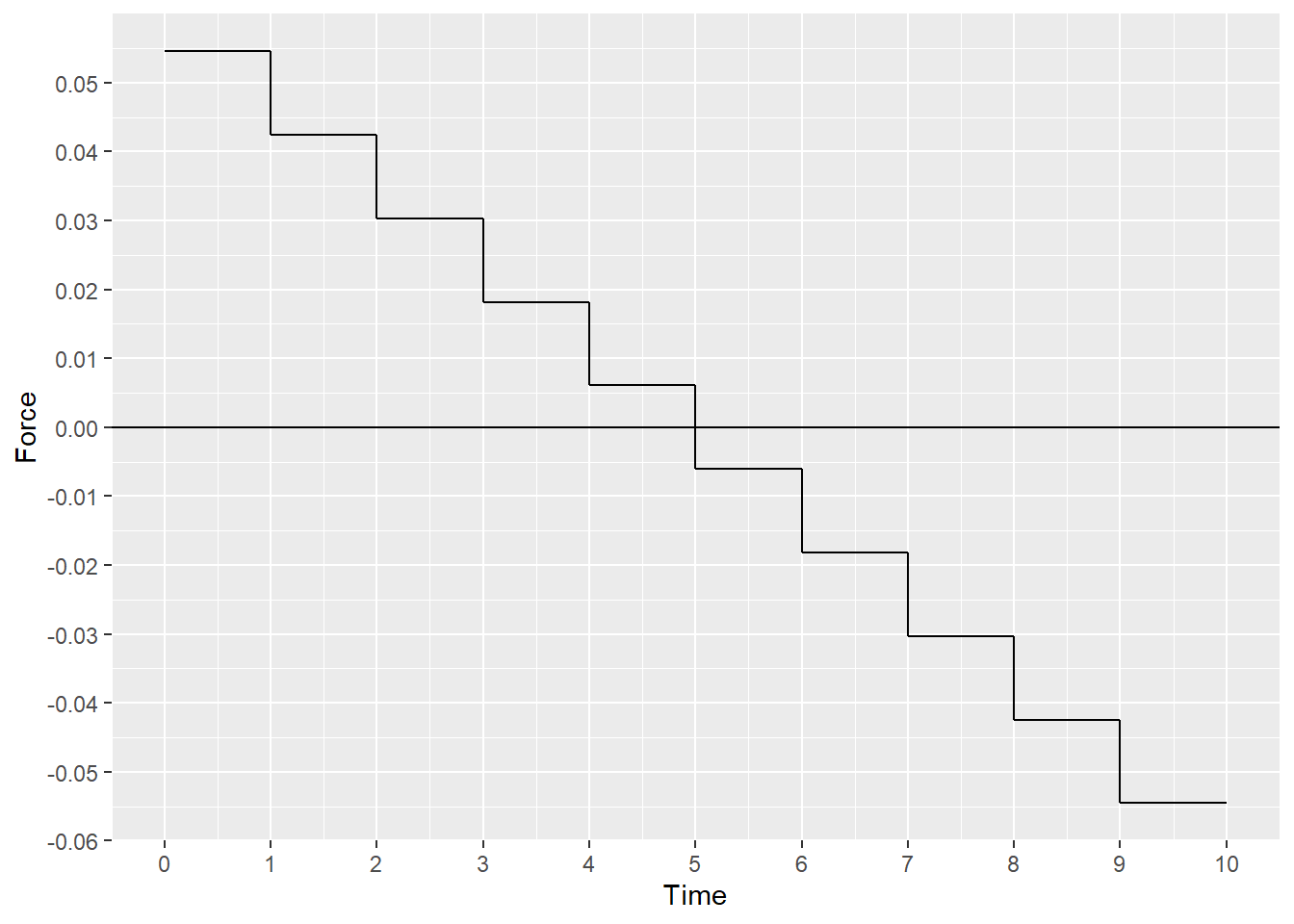
theta <- solve(a = R0) %*% b0
theta [,1]
[1,] 0.054545455
[2,] 0.042424242
[3,] 0.030303030
[4,] 0.018181818
[5,] 0.006060606
[6,] -0.006060606
[7,] -0.018181818
[8,] -0.030303030
[9,] -0.042424242
[10,] -0.054545455ggplot() +
geom_step(mapping = aes(x = seq(11) - 1, y = c(theta, tail(theta, 1))), direction = "hv") +
scale_x_continuous(breaks = scales::pretty_breaks(10)) +
scale_y_continuous(breaks = scales::pretty_breaks(10)) +
geom_hline(yintercept = 0) +
labs(x = "Time", y = "Force")\(v^{\textrm{fin}}=0\)
C[1, ] %*% theta [,1]
[1,] -0.0000000000000001595946\(p^{\textrm{fin}}=1\)
C[2, ] %*% theta [,1]
[1,] 1\(\|f^{\textrm{least norm}}\|^2\)
theta %>%
norm(type = "2") %>%
{
.^2
}[1] 0.0121212116 Constrained least squares > 16.2 Solution (p.344)
Optimality conditions via Lagrange multipliers. (p.344)
\(\textbf{Cx}=\textbf{d}\)を制約として、\(\|\textbf{Ax}-\textbf{b}\|^2\)が最小となる\(\hat{\textbf{x}}\)を求める。
ここで\(\textbf{A}\)は\((m\times n)\)行列、\(\textbf{b}\)は\(m\)次元ベクトル\(\begin{bmatrix}b_1\cdots b_m\end{bmatrix}^{T}\)、\(\textbf{C}\)は\((p\times n)\)行列、\(\textbf{d}\)は\(p\)次元ベクトル\(\begin{bmatrix}d_1\cdots d_p\end{bmatrix}^{T}\)、\(\textbf{c}^{T}_i\)は\(\textbf{C}\)の\(i\)行目、\(\textbf{x}\)は\(n\)次元ベクトル\(\begin{bmatrix}x_1\cdots x_n\end{bmatrix}^{T}\)。
ラグランジュ乗数を\(p\)次元ベクトル\(\textbf{z}=\begin{bmatrix}z_1\cdots z_p\end{bmatrix}\)とすると、ラグランジュ関数は \[L(\textbf{x},\textbf{z})=\|\textbf{Ax}-\textbf{b}\|^2+z_1(\textbf{c}^{T}_1\textbf{x}-d_1)+\cdots+z_p(\textbf{c}^{T}_p\textbf{x}-d_p)\]
\(\hat{\textbf{x}}\)が上記制約のもとでの最小化解ならば、推定されたラグランジュ乗数\(\hat{\textbf{z}}\)は \[\dfrac{\partial L}{\partial x_i}\left(\hat{\textbf{x}},\hat{\textbf{z}}\right)=0,\quad i=1,\cdots,n\]および\[\dfrac{\partial L}{\partial z_i}\left(\hat{\textbf{x}},\hat{\textbf{z}}\right)=0,\quad i=1,\cdots,p\]を満たす。
後者は\[\dfrac{\partial L}{\partial z_i}\left(\hat{\textbf{x}},\hat{\textbf{z}}\right)=\textbf{c}^{T}_i\hat{\textbf{x}}-d_i=0,\quad i=1,\cdots,p\]と表され、\(\hat{\textbf{x}}\)は\[\textbf{C}\hat{\textbf{x}}=\textbf{d}\]を満たす。
前者は最小化を求める\[\|\textbf{Ax}-\textbf{b}\|^2=\displaystyle\sum_{i=1}^m\left(\displaystyle\sum_{j=1}^n\textbf{A}_{ij}\textbf{x}_j-\textbf{b}_i\right)^2\]を\(x_i\)で偏微分して
\[\dfrac{\partial L}{\partial x_i}\left(\hat{\textbf{x}},\hat{\textbf{z}}\right)=2\displaystyle\sum_{j=1}^n\left(\textbf{A}^{T}\textbf{A}\right)_{ij}\hat{x}_j-2\left(\textbf{A}^{T}\textbf{b}\right)_i+\displaystyle\sum_{j=1}^p{\hat{\textbf{z}}_j(\textbf{c}_j)_i}=0\]と変形し、行列表現にすると、\[2\left(\textbf{A}^{T}\textbf{A}\right)\hat{x}-2\textbf{A}^{T}\textbf{b}+\textbf{C}^{T}\hat{\textbf{z}}=0\]と表せられる。
ここに制約条件\[\textbf{C}\hat{\textbf{x}}=\textbf{d}\]を組み合わせると、次の\((n+p)\)元連立方程式となる。 \[\begin{bmatrix}2\textbf{A}^{T}\textbf{A} & \textbf{C}^{T}\\\textbf{C}&\textbf{0}\end{bmatrix}\begin{bmatrix}\hat{\textbf{x}}\\\hat{\textbf{z}}\end{bmatrix}=\begin{bmatrix}2\textbf{A}^{T}\textbf{b}\\\textbf{d}\end{bmatrix}\]
これはカルーシュ・クーン・タッカー条件(KKT matrix)と呼ばれ、制約なしの場合の正規方程式の拡張であり、制約付き最小二乗法問題は変数が\((n+p)\)個の\((n+p)\)連立方程式を解くことになる。
Invertibility of KKT matrix. (p.345)
また上記\((n+p)\times(n+p)\)行列はカルーシュ・クーン・タッカー行列と呼ばれ、\(\textbf{C}\)の行が線形独立かつ\(\begin{bmatrix}\textbf{A}\\\textbf{C}\end{bmatrix}\)の列が線形独立の場合に限り、逆行列を持つ。
なお\(\textbf{C}\)の行が線形独立であるには\(\textbf{C}\)は横長行列または正方行列(\(p\leq n\))である必要があり、\(\textbf{A}\)の列が線形独立の場合でも、\(\begin{bmatrix}\textbf{A}\\\textbf{C}\end{bmatrix}\)の列が線形独立となることがある。
\[\begin{bmatrix}\hat{\textbf{x}}\\\hat{\textbf{z}}\end{bmatrix}=\begin{bmatrix}2\textbf{A}^{T}\textbf{A} & \textbf{C}^{T}\\\textbf{C}&\textbf{0}\end{bmatrix}^{-1}\begin{bmatrix}2\textbf{A}^{T}\textbf{b}\\\textbf{d}\end{bmatrix}\]
上記式より\(\hat{\textbf{x}}\)は\(\textbf{b},\,\textbf{d}\)の線形関数となることがわかる。
16 Constrained least squares > 16.3 Solving constrained least squares problems (p.347)
Solving constrained least squares problems via QR factorization. (p.348)
次に\(\pmb{\omega}=\hat{\textbf{z}}-2\textbf{d}\)とし、カルーシュ・クーン・タッカー条件を変形する。 \[\begin{aligned} &2\left(\textbf{A}^{T}\textbf{A}\right)\hat{\textbf{x}}+\textbf{C}^{T}\hat{\textbf{z}}\\ &=2\left(\textbf{A}^{T}\textbf{A}\right)\hat{\textbf{x}}+\textbf{C}^{T}(\pmb{\omega}+2\textbf{d})\\ &=2\left(\textbf{A}^{T}\textbf{A}\right)\hat{\textbf{x}}+\textbf{C}^{T}\pmb{\omega}+\textbf{C}^{T}2\textbf{d}\\ &=2\left(\textbf{A}^{T}\textbf{A}\right)\hat{\textbf{x}}+\textbf{C}^{T}\pmb{\omega}+\textbf{C}^{T}2\textbf{C}\hat{\textbf{x}}\\ &=2\left(\textbf{A}^{T}\textbf{A}+\textbf{C}^{T}\textbf{C}\right)\hat{\textbf{x}}+\textbf{C}^{T}\pmb{\omega}\\ &=2\textbf{A}^{T}\textbf{b},\quad \textbf{C}\hat{\textbf{x}}=\textbf{d}\end{aligned}\]
Step 1
続いて\(\begin{bmatrix}\textbf{A}\\\textbf{C}\end{bmatrix}\)をQR分解し、さらに\(\textbf{Q}\)を\(\textbf{Q}_1(m\times n)\)と\(\textbf{Q}_2(p\times n)\)に分割する。\[\begin{bmatrix}\textbf{A}\\\textbf{C}\end{bmatrix}=\textbf{QR}=\begin{bmatrix}\textbf{Q}_1\\\textbf{Q}_2\end{bmatrix}\textbf{R}\]
その後\(\textbf{A}=\textbf{Q}_1\textbf{R}\)、\(\textbf{C}=\textbf{Q}_2\textbf{R}\)および \[\begin{aligned} \textbf{A}^{T}\textbf{A}+\textbf{C}^{T}\textbf{C}&=(\textbf{Q}_1\textbf{R})^{T}(\textbf{Q}_1\textbf{R})+(\textbf{Q}_2\textbf{R})^{T}(\textbf{Q}_2\textbf{R})\\ &=\textbf{R}^{T}\textbf{Q}_1^{T}\textbf{Q}_1\textbf{R}+\textbf{R}^{T}\textbf{Q}_2^{T}\textbf{Q}_2\textbf{R}\\ &=\textbf{R}^{T}\left(\textbf{Q}_1^{T}\textbf{Q}_1+\textbf{Q}_2^{T}\textbf{Q}_2\right)\textbf{R}\\ &=\textbf{R}^{T}\left(\textbf{Q}^{T}\textbf{Q}\right)\textbf{R}\\ &=\textbf{R}^{T}\textbf{I}\textbf{R}=\textbf{R}^{T}\textbf{R} \end{aligned}\]を代入して、 \[2\textbf{R}^{T}\textbf{R}\hat{\textbf{x}}+\textbf{R}^{T}\textbf{Q}_2^T\omega=2\textbf{R}^T\textbf{Q}_1^T\textbf{b},\quad \textbf{Q}_2\textbf{R}\hat{\textbf{x}}=\textbf{d}\]が得られる。
- \(\textbf{Q}\)は直交行列であるため\(\textbf{Q}^T\textbf{Q}=\textbf{I}\)
\(\textbf{Q}_1^{T}\textbf{Q}_1+\textbf{Q}_2^{T}\textbf{Q}_2=\textbf{Q}^{T}\textbf{Q}\)の例
Q <- sample(seq(100), 36, replace = F) %>% matrix(nrow = 6)
Q1 <- Q[1:4, ] # 4行6列
Q2 <- Q[5:6, ] # 2行6列
a <- (t(Q1) %*% Q1) + (t(Q2) %*% Q2)
b <- t(Q) %*% Q
a == b [,1] [,2] [,3] [,4] [,5] [,6]
[1,] TRUE TRUE TRUE TRUE TRUE TRUE
[2,] TRUE TRUE TRUE TRUE TRUE TRUE
[3,] TRUE TRUE TRUE TRUE TRUE TRUE
[4,] TRUE TRUE TRUE TRUE TRUE TRUE
[5,] TRUE TRUE TRUE TRUE TRUE TRUE
[6,] TRUE TRUE TRUE TRUE TRUE TRUE前者の式に左から\(\left(\textbf{R}^T\right)^{-1}\)を乗じると、
\[\begin{aligned} \left(\textbf{R}^T\right)^{-1}\left(2\textbf{R}^{T}\textbf{R}\hat{\textbf{x}}+\textbf{R}^{T}\textbf{Q}_2^T\omega\right)&=\left(\textbf{R}^T\right)^{-1}2\textbf{R}^T\textbf{Q}_1^T\textbf{b}\\ \left(\textbf{R}^T\right)^{-1}\left(2\textbf{R}^{T}\textbf{R}\hat{\textbf{x}}\right)+\left(\textbf{R}^T\right)^{-1}\left(\textbf{R}^{T}\textbf{Q}_2^T\omega\right)&=2\left(\textbf{R}^T\right)^{-1}\textbf{R}^T\textbf{Q}_1^T\textbf{b}\\ 2\left(\textbf{R}^T\right)^{-1}\textbf{R}^{T}\textbf{R}\hat{\textbf{x}}+\left(\textbf{R}^T\right)^{-1}\textbf{R}^{T}\textbf{Q}_2^T\omega&=2\textbf{I}\textbf{Q}_1^T\textbf{b}\\ 2\textbf{I}\textbf{R}\hat{\textbf{x}}+\textbf{I}\textbf{Q}_2^T\omega&=2\textbf{I}\textbf{Q}_1^T\textbf{b}\\ \textbf{R}\hat{\textbf{x}}&=\textbf{I}\textbf{Q}_1^T\textbf{b}-(1/2)\textbf{I}\textbf{Q}_2^T\omega\\ \textbf{R}\hat{\textbf{x}}&=\textbf{Q}_1^T\textbf{b}-(1/2)\textbf{Q}_2^T\omega\\ \end{aligned}\]
これを\(\textbf{C}\hat{\textbf{x}}=\textbf{d}\)に代入すると、 \[\textbf{C}\hat{\textbf{x}}=\textbf{Q}_2\textbf{R}\hat{\textbf{x}}=\textbf{Q}_2\left(\textbf{Q}_1^T\textbf{b}-(1/2)\textbf{Q}_2^T\omega\right)=\textbf{Q}_2\textbf{Q}_1^T\textbf{b}-\textbf{Q}_2(1/2)\textbf{Q}_2^T\omega=\textbf{d}\]より、\[\textbf{Q}_2\textbf{Q}_2^T\omega=2\textbf{Q}_2\textbf{Q}_1^T\textbf{b}-2\textbf{d}\]
- \(\begin{bmatrix}\textbf{A}\\\textbf{C}\end{bmatrix}\)の列ベクトルは線形独立(フルランク)を仮定しているため、そのQR分解による行列Rは、対角成分が非ゼロ(すべて正の値)であり、行列式(対角成分の積)もゼロではなく、つまり特異行列ではない(正則行列である)。よってRの逆行列は存在し、Rの転置の逆行列(Rのランクは変わらない)も存在する。
Step 2
次に\(\textbf{Q}_2^T\)(線形独立の行列(証明はVMLSのp.348)。故に以下の\(\tilde{\textbf{R}}\)は逆行列を持つ)をQR分解し、\(\textbf{Q}_2^T=\tilde{\textbf{Q}}\tilde{\textbf{R}}\Leftrightarrow \textbf{Q}_2=\tilde{\textbf{R}}^T\tilde{\textbf{Q}}^T\)を代入すると
\[\begin{aligned} \textbf{Q}_2\textbf{Q}_2^T\omega&=2\textbf{Q}_2\textbf{Q}_1^T\textbf{b}-2\textbf{d}\\ \tilde{\textbf{R}}^T\tilde{\textbf{Q}}^T\tilde{\textbf{Q}}\tilde{\textbf{R}}\omega&=2\tilde{\textbf{R}}^T\tilde{\textbf{Q}}^T\textbf{Q}_1^T\textbf{b}-2\textbf{d}\\ \tilde{\textbf{R}}^T\textbf{I}\tilde{\textbf{R}}\omega&=2\tilde{\textbf{R}}^T\tilde{\textbf{Q}}^T\textbf{Q}_1^T\textbf{b}-2\textbf{d}\\ \tilde{\textbf{R}}^T\tilde{\textbf{R}}\omega&=2\tilde{\textbf{R}}^T\tilde{\textbf{Q}}^T\textbf{Q}_1^T\textbf{b}-2\textbf{d}\\ \left(\tilde{\textbf{R}}^T\right)^{-1} \tilde{\textbf{R}}^T\tilde{\textbf{R}}\omega&=2\left(\tilde{\textbf{R}}^T\right)^{-1}\tilde{\textbf{R}}^T\tilde{\textbf{Q}}^T\textbf{Q}_1^T\textbf{b}-2\left(\tilde{\textbf{R}}^T\right)^{-1}\textbf{d}\\ \textbf{I}\tilde{\textbf{R}}\omega&=2\textbf{I}\tilde{\textbf{Q}}^T\textbf{Q}_1^T\textbf{b}-2\left(\tilde{\textbf{R}}^T\right)^{-1}\textbf{d}\\ \tilde{\textbf{R}}\omega&=2\tilde{\textbf{Q}}^T\textbf{Q}_1^T\textbf{b}-2\left(\tilde{\textbf{R}}^T\right)^{-1}\textbf{d}\\ \end{aligned}\] が得られる。
\(\textbf{Q}_2^T=\tilde{\textbf{Q}}\tilde{\textbf{R}}\Leftrightarrow\textbf{Q}_2=\tilde{\textbf{R}}^T\tilde{\textbf{Q}}^T\)の例
A <- sample(seq(100), 36, replace = F) %>% matrix(nrow = 6)
QR <- qr(t(A))
Q <- qr.Q(QR)
R <- qr.R(QR)
list(A_t = t(A), QR = Q %*% R, A = A, R_tQ_t = t(R) %*% t(Q))$A_t
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 3 8 17 1 18 21
[2,] 46 100 14 97 62 27
[3,] 7 43 36 24 68 88
[4,] 55 73 86 98 28 50
[5,] 31 15 38 45 64 49
[6,] 16 41 80 87 57 76
$QR
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 3 8 17 1 18 21
[2,] 46 100 14 97 62 27
[3,] 7 43 36 24 68 88
[4,] 55 73 86 98 28 50
[5,] 31 15 38 45 64 49
[6,] 16 41 80 87 57 76
$A
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 3 46 7 55 31 16
[2,] 8 100 43 73 15 41
[3,] 17 14 36 86 38 80
[4,] 1 97 24 98 45 87
[5,] 18 62 68 28 64 57
[6,] 21 27 88 50 49 76
$R_tQ_t
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 3 46 7 55 31 16
[2,] 8 100 43 73 15 41
[3,] 17 14 36 86 38 80
[4,] 1 97 24 98 45 87
[5,] 18 62 68 28 64 57
[6,] 21 27 88 50 49 76Step 3
上記の通り\(\textbf{Q}_2^T\)は線形独立であるため、そのQR分解の行列Rの行列式は非ゼロ、逆行列を持つ。
そこで始めに\[\left(\tilde{\textbf{R}}^T\right)\left(\left(\tilde{\textbf{R}}^T\right)^{-1}\textbf{d}\right)=\textbf{d}\]から\(\left(\tilde{\textbf{R}}^T\right)^{-1}\textbf{d}\)からを求め、
Step 4
求めた\(\left(\tilde{\textbf{R}}^T\right)^{-1}\textbf{d}\)を\[\tilde{\textbf{R}}\omega=2\tilde{\textbf{Q}}^T\textbf{Q}_1^T\textbf{b}-2\left(\tilde{\textbf{R}}^T\right)^{-1}\textbf{d}\]に代入して\(\omega\)を求める。
Step 5
最後に求めた\(\omega\)を\[\textbf{R}\hat{\textbf{x}}=\textbf{Q}_1^T\textbf{b}-(1/2)\textbf{Q}_2^T\omega\]に代入して\(\hat{\textbf{x}}\)を求める。
17 Constrained least squares applications > 17.1 Portfolio optimization > 17.1.3 Example (p.362)
# R:2000日分(8年)の日次リターン。1:19列は19銘柄のリターン。20列はリスクフリー資産のリターン(年間リターン1%。250*(4/10^5)=0.01)
# Rtest:Rとは異なる500日分(2年)の日次リターン。
# 列:銘柄(n)、行:日(T)
lapply(list(R, Rtest), dim)[[1]]
[1] 2000 20
[[2]]
[1] 500 20ハイリターン・ローリスクの資産アロケーション(\(w\))を求める。
\(T\)をピリオド、\(\rho\)を望むポートフォリオリターン、\(\mu=R^T\,\textbf{1}/T\)は各銘柄毎の\(T\)期間における平均リターン(n次元ベクトル)とすると、\(\rho\)は、
\[\textbf{avg}(r)=(1/T)\,\textbf{1}^T\,(Rw)=\mu^Tw=\rho\]
と表せられ、リスク(標準偏差)の2乗は \[\textbf{std}(r)^2=(1/T)\|r-\textbf{avg}(r)\textbf{1}\|^2=(1/T)\|r-\rho\textbf{1}\|^2\]となる。
ポートフォリオリターン\(\rho\)の制約のもと、リスクの2乗を最小化するとは \[\begin{bmatrix}\textbf{1}^T\\\mu^T\end{bmatrix}w=\begin{bmatrix}1\\\rho\end{bmatrix}\]の制約のもと\[\|Rw-\rho\textbf{1}\|\]を最小化することである。
なお\(1/T\)は結果に影響しないため含めない。
上段は各銘柄への割当ウエイトの合計が1になることを、下段は平均ポートフォリオリターンが\(\rho\)になる制約を表している。
つまりポートフォリオ最適化問題は以下の式を解くことになる。 \[\begin{bmatrix}w\\z_1\\z_2\end{bmatrix}=\begin{bmatrix}2R^TR&1&\mu\\\textbf{1}^T&0&0\\\mu^T&0&0\end{bmatrix}^{-1}\begin{bmatrix}2\rho T\mu\\1\\\rho\end{bmatrix}\]
# ハイリターン・ローリスクな w(ポートフォリオウエイト) を求める(パレート最適)。
# ポートフォリオウエイト算出関数
func_w <- function(R, rho) {
T <- nrow(R)
n <- ncol(R)
# 銘柄毎の平均リターン
mu <- apply(R, 2, sum) / T
# 右辺第一因子
KKT_c1 <- cbind(2 * t(R) %*% R, rep(1, n), mu)
KKT_c2 <- c(rep(1, n), 0, 0)
KKT_c3 <- c(mu, 0, 0)
KKT <- rbind(KKT_c1, KKT_c2, KKT_c3)
dim(KKT)
# 右辺第二因子
b <- c(2 * rho * T * mu, 1, rho) %>% matrix(ncol = 1)
dim(b)
# ポートフォリオウエイト
w_z1_z2 <- func_solve(A = KKT, b = b)
w <- head(w_z1_z2, n)
return(w)
}
# QR分解によるxの推定量算出関数(Ax=b)
func_solve <- function(A, b) {
QR <- qr(x = A)
Q <- qr.Q(QR)
R <- qr.R(QR)
b_tilde <- t(Q) %*% b
x_hat <- solve(R) %*% b_tilde
return(x_hat)
}
# total valueを求める関数
func_total_value <- function(R, rho, days) {
# 年間営業日を days 日とし、rho %の年間リターンを求める
w <- func_w(R = R, rho = rho / 100 / days)
# ポートフォリオリターンの時系列推移
r <- R %*% w
# 年換算ポートフォリオリターン
pf_return <- days * mean(r)
# 年換算ポートフォリオリスク
# pf_risk <- days^0.5*sd(r) # 不偏標準偏差
pf_risk <- days^0.5 * sqrt(var(r) * (length(r) - 1) / length(r)) # 標本標準偏差
# トータル資産価値。リターンの累積積(複利)
v <- cumprod(1 + r) * 10000
return(list(w = w, r = r, v = v, pf_return = pf_return, pf_risk = pf_risk))
}days <- 250
# 年間リターン 10%
rho <- 10
tmp <- func_total_value(R = R, rho = rho, days = days)
w10 <- tmp$w
v10 <- tmp$v
pf_return10 <- tmp$pf_return
pf_risk10 <- tmp$pf_risk
# テストデータ
r10_test <- Rtest %*% w10
v10_test <- cumprod(1 + r10_test) * 10000
pf_return10_test <- days * mean(r10_test)
pf_risk10_test <- days^0.5 * sqrt(var(r10_test) * (length(r10_test) - 1) / length(r10_test))
# 年間リターン 20%
rho <- 20
tmp <- func_total_value(R = R, rho = rho, days = days)
w20 <- tmp$w
v20 <- tmp$v
pf_return20 <- tmp$pf_return
pf_risk20 <- tmp$pf_risk
# テストデータ
r20_test <- Rtest %*% w20
v20_test <- cumprod(1 + r20_test) * 10000
pf_return20_test <- days * mean(r20_test)
pf_risk20_test <- days^0.5 * sqrt(var(r20_test) * (length(r20_test) - 1) / length(r20_test))
# 年間リターン 40%
rho <- 40
tmp <- func_total_value(R = R, rho = rho, days = days)
w40 <- tmp$w
v40 <- tmp$v
pf_return40 <- tmp$pf_return
pf_risk40 <- tmp$pf_risk
# テストデータ
r40_test <- Rtest %*% w40
v40_test <- cumprod(1 + r40_test) * 10000
pf_return40_test <- days * mean(r40_test)
pf_risk40_test <- days^0.5 * sqrt(var(r40_test) * (length(r40_test) - 1) / length(r40_test))
# 年間リターン 1%
rho <- 1
tmp <- func_total_value(R = R, rho = rho, days = days)
w01 <- tmp$w
v01 <- tmp$v
pf_return01 <- tmp$pf_return
pf_risk01 <- tmp$pf_risk
# テストデータ
r01_test <- Rtest %*% w01
v01_test <- cumprod(1 + r01_test) * 10000
pf_return01_test <- days * mean(r01_test)
pf_risk01_test <- days^0.5 * sqrt(var(r01_test) * (length(r01_test) - 1) / length(r01_test))
# 均等に割り振った場合のリターン
w_uni <- (1 / ncol(R)) * rep(1, ncol(R))
r_uni <- R %*% w_uni
v_uni <- cumprod(1 + r_uni) * 10000
pf_return_uni <- days * mean(r_uni)
pf_risk_uni <- days^0.5 * sd(r_uni)
# テストデータ
r_uni_test <- Rtest %*% w_uni
v_uni_test <- cumprod(1 + r_uni_test) * 10000
pf_return_uni_test <- days * mean(r_uni_test)
pf_risk_uni_test <- days^0.5 * sqrt(var(r_uni_test) * (length(r_uni_test) - 1) / length(r_uni_test))# 確認
sapply(list(w10, w20, w40, w01, w_uni), sum)[1] 1 1 1 1 1result <- rbind(
c(pf_return01, pf_return01_test, pf_risk01, pf_risk01_test),
c(pf_return10, pf_return10_test, pf_risk10, pf_risk10_test),
c(pf_return20, pf_return20_test, pf_risk20, pf_risk20_test),
c(pf_return40, pf_return40_test, pf_risk40, pf_risk40_test),
c(pf_return_uni, pf_return_uni_test, pf_risk_uni, pf_risk_uni_test)
) %>% round(2)
row.names(result) <- c("1%", "10%", "20%", "40%", "1/n")
colnames(result) <- c("Return Train", "Return Test", "Risk Train", "Risk Tes")
result Return Train Return Test Risk Train Risk Tes
1% 0.01 0.01 0.00 0.00
10% 0.10 0.08 0.09 0.07
20% 0.20 0.15 0.18 0.15
40% 0.40 0.30 0.37 0.31
1/n 0.10 0.21 0.23 0.13columnname <- c("40%", "20%", "10%", "1 / n", "1%")
#
df <- data.frame(Day = seq(nrow(R)), v40, v20, v10, v_uni, v01) %>%
{
colnames(.)[-1] <- columnname
.
} %>%
gather(key = "key", value = "Value", colnames(.)[-1])
df$key <- df$key %>% factor(levels = columnname)
g1 <- df %>%
ggplot(mapping = aes(x = Day, y = Value, col = key)) +
geom_line() +
labs(title = "Training") +
theme(
legend.title = element_blank(),
legend.position = "top"
)
#
df <- data.frame(Day = seq(nrow(Rtest)), v40_test, v20_test, v10_test, v_uni_test, v01_test) %>%
{
colnames(.)[-1] <- columnname
.
} %>%
gather(key = "key", value = "Value", colnames(.)[-1])
df$key <- df$key %>% factor(levels = columnname)
g2 <- df %>%
ggplot(mapping = aes(x = Day, y = Value, col = key)) +
geom_line() +
labs(title = "Test") +
theme(
legend.title = element_blank(),
legend.position = "top"
)
#
risk_return <- data.frame(
Risk = R %>% apply(
MARGIN = 2,
function(x) days^0.5 * sqrt(var(x) * (length(x) - 1) / length(x))
),
Return = R %>% apply(MARGIN = 2, function(x) days * mean(x))
)
g3 <- ggplot() +
geom_point(data = risk_return, mapping = aes(x = Risk, y = Return)) +
geom_point(mapping = aes(x = result[, 3], y = result[, 1]), col = "red") +
geom_text(
mapping = aes(x = result[, 3], y = result[, 1], label = row.names(result)),
hjust = 0.5, vjust = 2
) +
labs(title = "Risk × Return")
arrangeGrob(g1, g2, g3, ncol = 1, nrow = 3, heights = c(1, 1, 1)) %>% ggpubr::as_ggplot()17 Constrained least squares applications > 17.2 Linear quadratic control (p.366)
状態を表す\(n\)次元ベクトル\(\textbf{x}_t\)、入力を表す\(m\)次元ベクトル\(\textbf{u}_t\)、システムの出力を\(p\)次元ベクトル\(\textbf{y}_t\)として、経時と共に変化する動的線形システム(線形時変系モデル)を解く。
\[\begin{aligned} \textbf{x}_{t+1}=\textbf{A}_t\textbf{x}_t+\textbf{B}_t\textbf{u}_t,\quad t=1,2,\cdots\\ \textbf{y}_t=\textbf{C}_t\textbf{x}_t,\quad t=1,2,\cdots \end{aligned}\]
- 多くの場合、\(m\leq n\)、\(p\leq n\)つまり入力と出力の次元が状態の次元以下である。
- 制御システムにおいて、入力\(\textbf{u}_t\)は、例えば航空機の動翼偏位(control surface deflections)やエンジン推力(engine thrust)のように、操作可能である。
- \(\textbf{x},\textbf{u},\textbf{y}\)を、例えば航空機の速度と高度の目標値からの偏差のように、「ある標準値または目標値からの偏差」とした場合、それらは小さい方が望ましい。
- 線形2次制御(linear quadratic control)は、上記2つの式の下、目的値の2乗(quadraticの理由)和を最小化するために、経時(\(t=1,\dots,T\))と共に変化する入力と状態遷移を選択することである。
- 多くの制御問題は初期状態拘束\(\textbf{x}_1=\textbf{x}^{\textrm{init}}\)が与えられ、終了状態拘束\(\textbf{x}_1=\textbf{x}^{\textrm{des}},\,\textrm{desired}\)が与えられる場合もある。
目的関数(objective function)は、 \[J=J_{\textrm{output}}+\rho J_{\textrm{input}}\]ここで、 \[\begin{aligned} J_{\textrm{output}}&=\|\textbf{y}_1\|^2+\cdots+\|\textbf{y}_T\|^2=\|\textbf{C}_1\textbf{x}_1\|^2+\cdots+\|\textbf{C}_T\textbf{x}_T\|^2\\ J_{\textrm{input}}&=\|\textbf{u}_1\|^2+\cdots+\|\textbf{u}_{T-1}\|^2 \end{aligned}\]
- 正の値を取るパラメータ\(\rho\)は入力 \(J_{\textrm{output}}\)に対する\(J_{\textrm{input}}\)のウエイト。
初期状態(\(\textbf{x}^{\textrm{init}}\))と終了状態(\(\textbf{x}^{\textrm{des}}\))を拘束とした線形2次制御(linear quadratic control)とは、制約を
\[ \textbf{x}_{t+1}=\textbf{A}_t\textbf{x}_t+\textbf{B}_t\textbf{u}_t,\quad \textbf{x}_1=\textbf{x}^{\textrm{init}},\quad \textbf{x}_T=\textbf{x}^{\textrm{des}},\quad t=1,\cdots,T-1 \]
として、入力と出力の合計(目的関数)\[J_{\textbf{output}}+\rho J_{\textbf{input}}\]の最小化(最適化)を探索すること。
- 説明変数は状態\(\textbf{x}_1,\dots,\textbf{x}_T\)および入力\(\textbf{u}_1,\dots,\textbf{u}_{T-1}\)
Formulation as constrained least squares problem. (p.367)
目的関数を展開すると、 \[\begin{aligned} J_{\textrm{output}}+\rho\,J_{\textrm{input}}&=\|\textbf{y}_1\|^2+\|\textbf{y}_2\|^2+\cdots+\|\textbf{y}_T\|^2+\rho\,\|\textbf{u}_1\|^2+\cdots+\rho\,\|\textbf{u}_{T-1}\|^2\\ &=\|\textbf{C}_1\textbf{x}_1\|^2+\|\textbf{C}_2\textbf{x}_2\|^2+\cdots+\|\textbf{C}_T\textbf{x}_T\|^2+\,\|\sqrt{\rho}\,\textbf{u}_1\|^2+\cdots+\,\|\sqrt{\rho}\,\textbf{u}_{T-1}\|^2\\ &=\|\textbf{C}_1\textbf{x}_1,\textbf{C}_2\textbf{x}_2,\cdots,\textbf{C}_T\textbf{x}_T,\sqrt{\rho}\,\textbf{u}_1,\cdots,\sqrt{\rho}\,\textbf{u}_{T-1}\|^2 \end{aligned}\]
ここで、説明変数(\(\textbf{x}_t,\,\textbf{u}_t\))ベクトルを\(Tn+(T-1)m\)次元ベクトル\(\textbf{z}=(\textbf{x}_1,\cdots,\textbf{x}_T,\textbf{u}_1,\cdots,\textbf{u}_{T-1})\)、目的関数の目標値を\(\tilde{b}=\textbf{0}\)、係数行列を\[\tilde{\textbf{A}}=\left[\begin{array}{cccc|ccc} \textbf{C}_1&&&&&&\\ &\textbf{C}_2&&&&&\\ &&\ddots&&&&\\ &&&\textbf{C}_T&&&\\ \hline &&&&\sqrt{\rho}\textbf{I}&&\\ &&&&&\ddots&\\ &&&&&&\sqrt{\rho}\textbf{I}\\ \end{array}\right]\]とすると、\[J_{\textrm{output}}+\rho\,J_{\textrm{input}}=\|\tilde{\textbf{A}}\textbf{z}\|^2\]の最適化とは \[\|\tilde{\textbf{A}}\textbf{z}-\tilde{\textbf{b}}\|^2\]の最小化。
- ブロック行列\(\tilde{\textbf{A}}\)の空白はすべてゼロ行列。上段は状態、下段は入力。
次に\(\textbf{x}_{t+1}=\textbf{A}_t\textbf{x}_t+\textbf{B}_t\textbf{u}_t\)で表せられる動的拘束(dynamics constraint)、そして初期状態拘束および終了状態拘束から
\[ \begin{aligned} &\textbf{x}_2 = \textbf{A}_1\textbf{x}_1+\textbf{B}_1\textbf{u}_1\\ &\textbf{x}_3 = \textbf{A}_2\textbf{x}_2+\textbf{B}_2\textbf{u}_2\\ &\quad\quad\quad\quad\vdots\\ &\textbf{x}_{T} = \textbf{A}_{T-1}\textbf{x}_{T-1}+\textbf{B}_{T-1}\textbf{u}_{T-1}\\ &\textbf{x}^{\textrm{init}}=\textbf{x}_1\\ &\textbf{x}^{\textrm{des}} =\textbf{x}_T \end{aligned} \]
変形して
\[ \begin{aligned} &\textbf{A}_1\textbf{x}_1-\textbf{I}\textbf{x}_2+\textbf{B}_1\textbf{u}_1=\textbf{0}\\ &\textbf{A}_2\textbf{x}_2-\textbf{I}\textbf{x}_3+\textbf{B}_2\textbf{u}_2=\textbf{0}\\ &\quad\quad\quad\quad\quad\vdots\\ &\textbf{A}_{T-1}\textbf{x}_{T-1}-\textbf{I}\textbf{x}_T+\textbf{B}_{T-1}\textbf{u}_{T-1}=\textbf{0}\\ &\textbf{Ix}_1=\textbf{x}^{\textrm{init}}\\ &\textbf{Ix}_T=\textbf{x}^{\textrm{des}}\\ \end{aligned} \]
行列形式にすると
\[ \left[\begin{array}{ccccc|cccc} \textbf{A}_1&-\textbf{I}&&&&\textbf{B}_1&&&\\ &\textbf{A}_2&-\textbf{I}&&&&\textbf{B}_1&&\\ &&\ddots&\ddots&&&&\ddots&\\ &&&\textbf{A}_{T-1}&-\textbf{I}&&&&\textbf{B}_{T-1}\\ \hline \textbf{I}&&&&&&&&\\ &&&&\textbf{I}&&&&\\ \end{array}\right] \begin{bmatrix} &\textbf{x}_1&\\ &\textbf{x}_2&\\ &\vdots&\\ &\textbf{u}_{T-1}&\\ \hline &\textbf{x}^{\textrm{init}}&\\ &\textbf{x}^{\textrm{des}}& \end{bmatrix} = \begin{bmatrix} &\textbf{0}&\\ &\textbf{0}&\\ &\vdots&\\ &\textbf{0}&\\ \hline &\textbf{x}^{\textrm{init}}&\\ &\textbf{x}^{\textrm{des}}& \end{bmatrix} \]
左辺第一因子と右辺をそれぞれ以下とすると、 \[\tilde{\textbf{C}}= \left[\begin{array}{ccccc|cccc} \textbf{A}_1&-\textbf{I}&&&&\textbf{B}_1&&&\\ &\textbf{A}_2&-\textbf{I}&&&&\textbf{B}_1&&\\ &&\ddots&\ddots&&&&\ddots&\\ &&&\textbf{A}_{T-1}&-\textbf{I}&&&&\textbf{B}_{T-1}\\ \hline \textbf{I}&&&&&&&&\\ &&&&\textbf{I}&&&&\\ \end{array}\right],\quad \tilde{\textbf{d}}= \begin{bmatrix} &\textbf{0}&\\ &\textbf{0}&\\ &\vdots&\\ &\textbf{0}&\\ \hline &\textbf{x}^{\textrm{init}}&\\ &\textbf{x}^{\textrm{des}}& \end{bmatrix}\]
拘束式は次の通り\[\tilde{\textbf{C}}\textbf{z}=\tilde{\textbf{d}}\]
ここでブロック行列\(\tilde{\textbf{C}}\)の空白はゼロ行列、垂直線は状態と入力を分割しており、水平線は線形動的方程式と初期状態および最終状態を分割している。
よって\[\tilde{\textbf{C}}z=\tilde{\textbf{d}}\]の制約のもと \[\|\tilde{\textbf{A}}\textbf{z}-\tilde{\textbf{b}}\|^2\]を最小化する制約付き最小二乗問題の解\(\tilde{\textbf{z}}\)は、最適化された入力軌跡とそれに伴う最適化された状態と出力を与える。
なお\(\tilde{\textbf{z}}\)は\(\tilde{\textbf{b}}\)および\(\tilde{\textbf{d}}\)の線形関数であり、\(\tilde{\textbf{b}}=\textbf{0}\)ならば、\(\textbf{x}^{\textrm{init}}\)および\(\textbf{x}^{\textrm{des}}\)の線形関数でもある。
17 Constrained least squares applications > 17.2 Linear quadratic control > 17.2.1 Example (p.368)
時不変系線形動的システム(\(\textbf{A,B,C}\)が不変)を考える。
本例では入力\(u_t\)、出力\(y_t\)はいずれもスカラーとし、各係数行列や初期拘束、終了拘束は次のチャンクのとおりとする。
始めに入力がゼロ(\(\textbf{u}_t\)を含めない)、かつ終了拘束も設けない場合(開ループ出力(open-loop output))を確認する。
\[y_t=\textbf{CA}^{t-1}\textbf{x}^{\textrm{init}},\quad t=1,\dots,T\]
A <- c(0.855, 1.161, 0.667, 0.015, 1.073, 0.053, -0.084, 0.059, 1.022) %>% matrix(ncol = 3, byrow = T)
B <- c(-0.076, -0.139, 0.342) %>% matrix(ncol = 1)
C <- c(0.218, -3.597, -1.683) %>% matrix(ncol = 3)
x_init <- c(0.496, -0.745, 1.394) %>% matrix(ncol = 1)
x_des <- rep(0, 3) %>% matrix(ncol = 1)
n <- ncol(A)
m <- ncol(B)
p <- nrow(C)
T <- 100
list(A = A, B = B, C = C, x_init = x_init, x_des = x_des)$A
[,1] [,2] [,3]
[1,] 0.855 1.161 0.667
[2,] 0.015 1.073 0.053
[3,] -0.084 0.059 1.022
$B
[,1]
[1,] -0.076
[2,] -0.139
[3,] 0.342
$C
[,1] [,2] [,3]
[1,] 0.218 -3.597 -1.683
$x_init
[,1]
[1,] 0.496
[2,] -0.745
[3,] 1.394
$x_des
[,1]
[1,] 0
[2,] 0
[3,] 0yol <- rep(0, T) %>% matrix(ncol = 1)
Xol <- cbind(x_init, rep(0, 3 * (T - 1)) %>% matrix(nrow = 3))
dim(yol)
dim(Xol)
Xol[, 1:10]
Xol[, 91:100][1] 100 1
[1] 3 100
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 0.496 0 0 0 0 0 0 0 0 0
[2,] -0.745 0 0 0 0 0 0 0 0 0
[3,] 1.394 0 0 0 0 0 0 0 0 0
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 0 0 0 0 0 0 0 0 0 0
[2,] 0 0 0 0 0 0 0 0 0 0
[3,] 0 0 0 0 0 0 0 0 0 0for (k in seq(T - 1)) {
Xol[, k + 1] <- A %*% Xol[, k] # 入力(Bu)無しの状態変数
}
yol <- C %*% Xol # システムの出力
t <- seq(T)
Output <- yol
ggplot(mapping = aes(x = t, y = Output)) +
geom_line()続いて入力(フィードバック)あり、かつ終了拘束を設ける場合。
func_constrained_least_squares_solve <- function(A, b, C, d) {
m <- nrow(A)
QR <- rbind(A, C) %>% qr(x = .)
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
Q1 <- head(Q, m)
Q2 <- tail(Q, -m)
QR <- qr(x = t(Q2))
Qtil <- qr.Q(qr = QR)
Rtil <- qr.R(qr = QR)
dim(Rtil)
dim(d)
w <- func_solve_linear_quations(
A = Rtil,
b = 2 * t(Qtil) %*% (t(Q1) %*% b) - 2 * func_solve_linear_quations(A = t(Rtil), b = d)
)
xhat <- func_solve_linear_quations(A = R, b = (t(Q1) %*% b - t(Q2) %*% w / 2))
return(xhat)
}
func_solve_linear_quations <- function(A, b) {
# Ax = b
QR <- qr(x = A)
Q <- qr.Q(qr = QR)
R <- qr.R(qr = QR)
btil <- t(Q) %*% b
x <- solve(a = R) %*% btil
return(x)
}
func_linear_quadratic_control <- function(A, B, C, x_init, x_des, T, rho) {
n <- nrow(A)
m <- ncol(B)
p <- nrow(C)
q <- ncol(x_init)
# A
Atil11 <- diag(1, T) %x% C # クロネッカー積. \tilde{A} の左上ブロック
Atil12 <- matrix(0, nrow = p * T, ncol = m * (T - 1)) # \tilde{A} の右上ブロック
Atil21 <- matrix(0, nrow = m * (T - 1), ncol = n * T) # \tilde{A} の左下ブロック
Atil22 <- sqrt(rho) * diag(1, nrow = m * (T - 1)) # \tilde{A} の右下ブロック
Atil <- rbind(cbind(Atil11, Atil12), cbind(Atil21, Atil22))
# b
btil <- matrix(0, nrow = p * T + m * (T - 1), ncol = q)
# C
Ctil11 <-
cbind(diag(1, T - 1) %x% A, matrix(0, nrow = n * (T - 1), ncol = n)) - cbind(
matrix(0, nrow = n * (T - 1), ncol = n),
diag(1, n * (T - 1))
)
Ctil12 <- diag(1, T - 1) %x% B
Ctil21 <-
rbind(cbind(diag(1, n), matrix(0, nrow = n, ncol = n * (T - 1))), cbind(
matrix(0, nrow = n, ncol = n * (T - 1)),
diag(1, n)
))
Ctil22 <- matrix(0, nrow = 2 * n, ncol = m * (T - 1))
Ctil <- rbind(cbind(Ctil11, Ctil12), cbind(Ctil21, Ctil22))
# d
dtil <- rbind(matrix(0, nrow = n * (T - 1), ncol = q), x_init, x_des)
#
z <- func_constrained_least_squares_solve(A = Atil, b = btil, C = Ctil, d = dtil)
x <- list()
for (i in seq(T)) {
x[[i]] <- z[((i - 1) * n + 1):(i * n), ]
}
# 入力
u <- list()
for (i in seq(T - 1)) {
u[[i]] <- z[(n * T + (i - 1) * m + 1):(n * T + i * m), ]
}
# 出力
y <- list()
for (i in seq(x)) {
y[[i]] <- C %*% x[[i]]
}
return(list(x = x, u = u, y = y))
}# p = 0.2とした場合
result <- func_linear_quadratic_control(A = A, B = B, C = C, x_init = x_init, x_des = x_des, T = T, rho = 0.2)
u <- result$u %>% unlist()
y <- result$y %>% unlist()
J_input <- norm(u, type = "2")^2
J_output <- norm(y, type = "2")^2
list(J_input = J_input, J_output = J_output)$J_input
[1] 0.7738943
$J_output
[1] 3.782999library(tidyr)
rho <- c(0.05, 0.2, 1)
df <- list()
cnt <- 1
for (i in seq(rho)) {
result <- func_linear_quadratic_control(A = A, B = B, C = C, x_init = x_init, x_des = x_des, T = T, rho = rho[i])
# 入力
tmp <- data.frame(t = seq(T - 1), ut = result$u %>% unlist())
colnames(tmp)[2] <- paste0(colnames(tmp)[2], " : p=", rho[i])
df[[cnt]] <- gather(data = tmp, key = "key", value = "value", colnames(tmp)[2])
cnt <- cnt + 1
# 出力
tmp <- data.frame(t = seq(T), yt = result$y %>% unlist())
colnames(tmp)[2] <- paste0(colnames(tmp)[2], " : p=", rho[i])
df[[cnt]] <- gather(data = tmp, key = "key", value = "value", colnames(tmp)[2])
cnt <- cnt + 1
}
tidydf <- Reduce(function(x, y) rbind(x, y), df)
ggplot(data = tidydf, mapping = aes(x = t, y = value, col = key)) +
geom_line() +
facet_wrap(facets = ~key, nrow = 2, scales = "fixed") +
theme(legend.position = "none", axis.title.y = element_blank())いずれの\(\rho\)の場合でも、\(y_t\)は終了拘束であるゼロに収束している。
17 Constrained least squares applications > 17.2 Linear quadratic control > 17.2.3 Linear state feedback control (p.371)
線形状態フィードバック制御(linear state feedback control)では各時点の状態を計測し、入力にフィードバックする。
\[\textbf{u}_t=K\textbf{x}_t\]
ここで\(t=1,2,\dots\)、 \(K\)は状態帰還利得行列(state feedback gain matrix. https://www.jstage.jst.go.jp/article/zisin/66/4/66_113/_pdf/-char/ja )。
以下は一つの例。
\(\textbf{x}^{\textrm{des}}=0\)の下、\(\hat{\textbf{z}}\)は制約付き線形最小二乗法の解。
\(\hat{\textbf{z}}\)は\(\textbf{x}^{\textrm{init}}\)と\(\textbf{x}^{\textrm{des}}\)の線形関数であり、\(\textbf{x}^{\textrm{des}}=0\)ととき、\(\hat{\textbf{z}}\)は\(\textbf{x}^{\textrm{init}}=\textbf{x}_1\)の線形関数。
\(\hat{\textbf{u}}_1\)(\(t=1\)のときの最適入力)は\(\hat{\textbf{z}}\)のサブベクトルであるので、\(\hat{\textbf{u}}_1\)は\(\textbf{x}_1\)の線形関数であり、故に\[\textbf{u}_1=K\textbf{x}_1\]となる。ここで\(K\)は\(m\times n\)行列。
\(K\)の列は初期状態を\(\textbf{x}^{\textrm{init}}=e_1,\dots,e_n\)として解くことができる。
Example. (p.372)
A <- c(0.855, 1.161, 0.667, 0.015, 1.073, 0.053, -0.084, 0.059, 1.022) %>% matrix(ncol = 3, byrow = T)
B <- c(-0.076, -0.139, 0.342) %>% matrix(ncol = 1)
C <- c(0.218, -3.597, -1.683) %>% matrix(ncol = 3)
x_init <- c(0.496, -0.745, 1.394) %>% matrix(ncol = 1)
x_des <- rep(0, 3) %>% matrix(ncol = 1)
T <- 100
rho <- 1
n <- nrow(A)# 線形状態フィードバック制御(simpler linear state feedback control)
# u_t = Kx_t
result <- func_linear_quadratic_control(
A = A, B = B, C = C,
x_init = diag(1, nrow = n), x_des = diag(0, nrow = n), T = T, rho = rho
)
usf <- result$u
K <- usf[[1]]
list(K = K)
TT <- 150
Xsf <- cbind(x_init, matrix(0, nrow = n, ncol = TT - 1))
for (k in seq(TT - 1)) {
Xsf[, k + 1] <- (A + B %*% K) %*% Xsf[, k]
}
usf <- K %*% Xsf[, seq(ncol(Xsf) - 1)]
ysf <- C %*% Xsf
# 線形2次制御(optimal)
result <- func_linear_quadratic_control(A = A, B = B, C = C, x_init = x_init, x_des = x_des, T = T, rho = rho)
u <- result$u %>% unlist()
y <- result$y %>% unlist()$K
[1] 0.3083288 -2.6586496 -1.4460229# 入力
u_optimal <- c(u, rep(0, TT - T))
u_state_feedback <- usf %>% as.vector()
# 出力
y_optimal <- c(y, rep(0, TT - T))
y_state_feedback <- ysf %>% as.vector()data.frame(t = seq(TT - 1), u_optimal, u_state_feedback, stringsAsFactors = F) %>%
gather(key = "key", value = "value", colnames(.)[-1]) %>%
ggplot(mapping = aes(x = t, y = value, col = key)) +
geom_line() +
labs(y = "u_t") +
theme(legend.title = element_blank())data.frame(t = seq(TT), y_optimal, y_state_feedback, stringsAsFactors = F) %>%
gather(key = "key", value = "value", colnames(.)[-1]) %>%
ggplot(mapping = aes(x = t, y = value, col = key)) +
geom_line() +
labs(y = "y_t") +
theme(legend.title = element_blank()) +
geom_hline(yintercept = 0, linetype = "dashed", col = "blue")線形2次制御では\(y_T\)はゼロに収束しているが、線形状態フィードバック制御では\(T\)迄にゼロに収束していない。
17 Constrained least squares applications > 17.3 Linear quadratic state estimation (p.372)
次の線形動的システムモデル(linear dynamical system)を考える。 \[\textbf{x}_{t+1}=\textbf{A}_t\textbf{x}_t+\textbf{B}_t\textbf{w}_t,\quad \textbf{y}_t=\textbf{C}_t\textbf{x}_t+\textbf{v}_t,\quad t=1,2,\dots\]
ここで、\(n\)次元ベクトル\(\textbf{x}_t\)はシステムの状態、\(p\)次元ベクトル\(\textbf{y}_t\)は計測値、\(m\)次元ベクトル\(\textbf{w}_t\)は入力またはプロセスノイズ、\(p\)次元ベクトル\(\textbf{v}_t\)は計測ノイズまたは残差、行列\(\textbf{A}_t,\,\textbf{B}_t,\,\textbf{C}_t\)はそれぞれ、動的、入力および出力係数行列。
\(\textbf{A}_t,\,\textbf{B}_t,\,\textbf{C}_t,\,\textbf{y}_t\quad t=1,\dots T\)は既知であり、プロセスまたは計測ノイズは未知、そして目的は状態\(\textbf{x}_1,\dots,\textbf{x}_T\)の推定である。
プロセスまたは計測ノイズは未知であるため、正確な状態シーケンスの推定は出来ず、上記の線形動的システムモデルを制約として状態シーケンス\(\textbf{x}_1,\dots,\textbf{x}_T\)とプロセスノイズシーケンス\(\textbf{w}_1,\dots,\textbf{w}_{T-1}\)を推定する。
状態シーケンスが推定できれば、計測ノイズは\(\textbf{v}_t=\textbf{y}_t-\textbf{C}_t\textbf{x}_t\)により推定できる。
始めに計測残差のノルムの2乗和を考える。 \[J_{\textrm{meas}}=\|\textbf{v}_1\|^2+\cdots+\|\textbf{v}_T\|^2=\|\textbf{C}_1\textbf{x}_1-\textbf{y}_1\|^2+\cdots+\|\textbf{C}_T\textbf{x}_T-\textbf{y}_T\|^2\]
この計測残差のノルムの2乗和が小さければ、推定した状態シーケンスと計測との間に矛盾はないと言える。
次にプロセスノイズのノルムの2乗和を考える。
\[J_{\textrm{proc}}=\|\textbf{w}_1\|^2+\cdots+\|\textbf{w}_{T-1}\|^2\]
プロセスノイズが小さければ\(J_{\textrm{proc}}\)も小さくなる。
Least squares state estimation. (p.373)
最小二乗状態推定とは、 \[\textbf{x}_{t+1}=\textbf{A}_t\textbf{x}_t+\textbf{B}_t\textbf{w}_t,\quad t=1,\dots,T-1\]の制約の下、 \[J_{\textrm{meas}}+\lambda J_{\textrm{proc}}\]を最小化する\(\textbf{x}_1,\dots,\textbf{x}_T\)および\(\textbf{w}_1,\dots,\textbf{w}_T\)を推測すること。
ここで\(\lambda\)は正の数値を取るパラメータ。
Formulation as constrained least squares problem. (p.374)
目的関数は \[\begin{aligned} J_{\textrm{meas}}+\lambda J_{\textrm{proc}} &=\|\textbf{C}_1\textbf{x}_1-\textbf{y}_1\|^2+\cdots+\|\textbf{C}_T\textbf{x}_T-\textbf{y}_T\|^2+\lambda\|\textbf{w}_1\|^2+\cdots+\lambda\|\textbf{w}_{T-1}\|^2\\ &=\|\textbf{C}_1\textbf{x}_1-\textbf{y}_1\|^2+\cdots+\|\textbf{C}_T\textbf{x}_T-\textbf{y}_T\|^2+\|\sqrt{\lambda}\textbf{w}_1\|^2+\cdots+\|\sqrt{\lambda}\textbf{w}_{T-1}\|^2\\ &=\|\textbf{C}_1\textbf{x}_1-\textbf{y}_1,\cdots,\textbf{C}_T\textbf{x}_T-\textbf{y}_T,\sqrt{\lambda}\textbf{w}_1,\cdots,\sqrt{\lambda}\textbf{w}_{T-1}\|^2 \end{aligned}\]
であり、ここで \[\textbf{z}=(\textbf{x}_1,\dots,\textbf{x}_T,\textbf{w}_1,\dots,\textbf{w}_{T-1})\]として行列形式にすると、
\[\left[\begin{array}{cccc|ccc} \textbf{C}_1&&&&&&\\ &\textbf{C}_2&&&&&\\ &&\ddots&&&&\\ &&&\textbf{C}_T&&&\\ \hline &&&&\sqrt{\lambda}\textbf{I}&&\\ &&&&&\ddots&\\ &&&&&&\sqrt{\lambda}\textbf{I}\\ \end{array}\right] \begin{bmatrix}\textbf{x}_1\\\textbf{x}_2\\\vdots\\\textbf{x}_T\\\hline\textbf{w}_1\\\vdots\\\textbf{w}_{T-1}\end{bmatrix} =\begin{bmatrix}\textbf{y}_1\\\textbf{y}_2\\\vdots\\\textbf{y}_T\\\hline \textbf{0}\\\vdots\\\textbf{0}\end{bmatrix}\]
ここで左辺第一因子を\(\tilde{\textbf{A}}\)、右辺を\(\tilde{\textbf{b}}\)とすると、 \[\|\tilde{\textbf{A}}\textbf{z}-\tilde{\textbf{b}}\|^2\]の最小化が最適化になる。
次に制約条件は
\[ \begin{aligned} &\textbf{x}_2 = \textbf{A}_1\textbf{x}_1+\textbf{B}_1\textbf{w}_1\\ &\textbf{x}_3 = \textbf{A}_2\textbf{x}_2+\textbf{B}_2\textbf{w}_2\\ &\quad\quad\quad\quad\vdots\\ &\textbf{x}_{T} = \textbf{A}_{T-1}\textbf{x}_{T-1}+\textbf{B}_{T-1}\textbf{w}_{T-1} \end{aligned} \]
を変形して
\[ \begin{aligned} &\textbf{A}_1\textbf{x}_1-\textbf{I}\textbf{x}_2+\textbf{B}_1\textbf{w}_1=\textbf{0}\\ &\textbf{A}_2\textbf{x}_2-\textbf{I}\textbf{x}_3+\textbf{B}_2\textbf{w}_2=\textbf{0}\\ &\quad\quad\quad\quad\quad\vdots\\ &\textbf{A}_{T-1}\textbf{x}_{T-1}-\textbf{I}\textbf{x}_T+\textbf{B}_{T-1}\textbf{w}_{T-1}=\textbf{0} \end{aligned} \]
行列形式にすると
\[ \left[\begin{array}{ccccc|cccc} \textbf{A}_1&-\textbf{I}&&&&\textbf{B}_1&&&\\ &\textbf{A}_2&-\textbf{I}&&&&\textbf{B}_1&&\\ &&\ddots&\ddots&&&&\ddots&\\ &&&\textbf{A}_{T-1}&-\textbf{I}&&&&\textbf{B}_{T-1}\\ \end{array}\right] \begin{bmatrix} &\textbf{x}_1&\\ &\textbf{x}_2&\\ &\vdots&\\ &\textbf{w}_{T-1}&\\ \end{bmatrix} = \begin{bmatrix} &\textbf{0}&\\ &\textbf{0}&\\ &\vdots&\\ &\textbf{0}&\\ \end{bmatrix} \]
左辺第一因子と右辺をそれぞれ\(\tilde{\textbf{C}}\)、\(\tilde{\textbf{d}}\)とすると、 \[\tilde{\textbf{C}}\textbf{z}=\tilde{\textbf{d}}\]
ここで\(\tilde{n}\)の次元は\(Tn+(T-1)m\)、\(\tilde{m}\)の次元は\(Tp+(T-1)m\)、\(\tilde{p}\)の次元は\((T-1)n\)。
17 Constrained least squares applications > 17.3 Linear quadratic state estimation > 17.3.1 Example (p.374)
# サンプル計測ノイズ
ymeas %>% dim()
ymeas[, 1:5]
ymeas[, 96:100][1] 2 100
[,1] [,2] [,3] [,4] [,5]
[1,] 17.07781 -18.392416 6.103945 -7.975072 2.273557
[2,] 16.38115 -1.021021 -2.621727 17.042102 -8.773949
[,1] [,2] [,3] [,4] [,5]
[1,] 284.7646 222.338 295.4026 260.8283 224.9874
[2,] -1631.7189 -1668.638 -1631.7075 -1655.4670 -1643.5822A <- rbind(cbind(diag(1, 2), diag(1, 2)), cbind(diag(0, 2), diag(1, 2)))
B <- rbind(diag(0, 2), diag(1, 2))
C <- cbind(diag(1, 2), diag(0, 2))
T <- 100
list(A = A, B = B, C = C)$A
[,1] [,2] [,3] [,4]
[1,] 1 0 1 0
[2,] 0 1 0 1
[3,] 0 0 1 0
[4,] 0 0 0 1
$B
[,1] [,2]
[1,] 0 0
[2,] 0 0
[3,] 1 0
[4,] 0 1
$C
[,1] [,2] [,3] [,4]
[1,] 1 0 0 0
[2,] 0 1 0 0func_linear_quadratic_estimation <- function(A, B, C, y, T, lambda) {
n <- nrow(A)
m <- ncol(B)
p <- nrow(C)
# A_tilde
Atil11 <- diag(1, T) %x% C # クロネッカー積. \tilde{A} の左上ブロック
Atil12 <- matrix(0, nrow = p * T, ncol = m * (T - 1)) # \tilde{A} の右上ブロック
Atil21 <- matrix(0, nrow = m * (T - 1), ncol = n * T) # \tilde{A} の左下ブロック
Atil22 <- sqrt(lambda) * diag(1, nrow = m * (T - 1)) # \tilde{A} の右下ブロック
Atil <- rbind(cbind(Atil11, Atil12), cbind(Atil21, Atil22))
# b_tilde
btil <- rbind(y %>% as.vector() %>% matrix(ncol = 1), diag(0, nrow = (T - 1) * m, ncol = 1))
# C_tilde
Ctila <- cbind(diag(1, T - 1) %x% A, matrix(0, nrow = n * (T - 1), ncol = n))
Ctilb <- cbind(diag(0, n * (T - 1), n), -diag(1, n * (T - 1)))
Ctil <- cbind(Ctila + Ctilb, diag(1, T - 1) %x% B)
# d_tilde
dtil <- diag(0, n * (T - 1), 1)
#
z <- func_constrained_least_squares_solve(A = Atil, b = btil, C = Ctil, d = dtil)
#
x <- list()
for (i in seq(T)) {
x[[i]] <- z[((i - 1) * n + 1):(i * n), ]
}
# 入力
u <- list()
for (i in seq(T - 1)) {
u[[i]] <- z[(n * T + (i - 1) * m + 1):(n * T + i * m), ]
}
# 出力
y <- list()
for (i in seq(x)) {
y[[i]] <- C %*% x[[i]]
}
return(list(x = x, u = u, y = y))
}
tidydf <- list()
cnt <- 1
for (lamb in c(1, 1000, 100000)) {
result <- func_linear_quadratic_estimation(A = A, B = B, C = C, y = ymeas, T = T, lambda = lamb)
y_hat <- result$y
tidydf[[cnt]] <- data.frame(
as.character(lamb),
sapply(y_hat, function(x) x[1, 1]),
sapply(y_hat, function(x) x[2, 1])
)
cnt <- cnt + 1
}
yhatdf <- Reduce(function(x, y) rbind(x, y), tidydf)
colnames(yhatdf) <- c("lambda", "x", "y")
ggplot() +
geom_point(mapping = aes(x = ymeas[1, ], y = ymeas[2, ])) +
geom_path(mapping = aes(x = x, y = y, col = lambda), data = yhatdf) +
geom_point(mapping = aes(x = x, y = y, col = lambda), data = yhatdf) +
labs(x = "", y = "")18 Nonlinear least squares > 18.1 Nonlinear equations and least squares > 18.1.1 Nonlinear equations (p.381)
各々\(n\)個の未知数(あるいは説明変数)を持つ\(m\)本の非線形方程式を考える。
\(f_i(x)\)を\(i\)番目の残差(residual)とし、ターゲットをゼロ(スカラー)に置く。
\[f_i(x)=0,\quad i=1,\dots,m\]
よって\(f_i:\textbf{R}^n\rightarrow\textbf{R}\)
もしゼロでない\(b_i\)をターゲットにする場合は(\(f_i(x)=b_i,\,\,i=1,\dots,m\))、\(\tilde{f}_i(x)=f_i(x)-b\)として、\(\tilde{f}_i(x)=0,\,\,i=1,\dots,m\)を解く。
コンパクトに表すと\[f(x)=\textbf{0},\quad f(x)=\left(f_1(x),\dots,f_m(x)\right)\]ここで右辺\(\textbf{0}\)は\(m\)次元ベクトル。
これは\(f\)を\(n\)次元ベクトルの\(m\)次元ベクトルへの射影\(f:\textbf{R}^n\rightarrow\textbf{R}^m\)、つまり\(m\)次元ベクトル\(f(x)\)を\(n\)次元ベクトル\(x\)の選択も基づく残差のベクトルとし、ゴールは残差がゼロとなる\(x\)を求めることになる。
\(f\)がアフィン関数であれば、\(n\)個の未知数を持つ\(m\)本の線形方程式のセットとして解くことができる(\(m>n\)ならば近似解)。
\(f\)がアフィン関数でない場合、
- 劣決定系(\(m<n\)、過小決定系、方程式数が未知数より少ない、under-determined,)
- 決定系(\(m=n\)、未知数と方程式数が同じ、square)
- 優決定系(\(m>n\)、過剰決定系、方程式数が未知数より多い、over-determined)
の考え方を非線形に拡張する。
18 Nonlinear least squares > 18.1 Nonlinear equations and least squares > 18.1.2 Nonlinear least squares (p.382)
決定系でない場合、\(f(x)=\textbf{0}\)の解が近似値となり、次の残差の自乗和を最小化する\(x\)(\(\hat{x}\))を探索する。
\[f_1(x)^2+\cdots+f_m(x)^2=\|f(x)\|^2\]
これはすべての\(x\)に対して\(\|f(x)\|^2\geq\|f(\hat{x})\|^2\)が成り立つことを意味し、その\(\hat{x}\)を非線形最小二乗法の解とする。
関数\(f\)がアフィン関数(『平行移動を伴う線型写像』. https://ja.wikipedia.org/wiki/%E3%82%A2%E3%83%95%E3%82%A3%E3%83%B3%E5%86%99%E5%83%8F )であれば、非線形最小二乗法は線形最小二乗法に帰着する。
18 Nonlinear least squares > 18.1 Nonlinear equations and least squares > 18.1.3 Optimality condition (p.382)
\(x_1,\dots,x_n\)それぞれでの\(\|f(x)\|^2\)を最小化する\(\hat{x}\)の条件は、\(\|f(x)\|^2\)の偏微分が\(\hat{x}\)でゼロになることである。
\[\dfrac{\partial}{\partial\,x_i}\|f(\hat{x})\|^2=0,\quad i=1,\dots,n\]
これは\[\nabla\|f(\hat{x})\|^2=0\]とも表せられる。
微分の線形性と合成関数の微分から、
\[\begin{aligned} \nabla\|f(x)\|^2 &=\nabla\left(\displaystyle\sum_{i=1}^m f_i(x)^2 \right) =\nabla\left(f_1(x)^2+\cdots+f_m(x)^2\right)\\ &=\nabla f_1(x)^2+\cdots+\nabla f_m(x)^2=2f_1(x)\nabla f_1(x)+\cdots+2f_m(x)\nabla f_m(x)\\ &=2\displaystyle\sum_{i=1}^mf_i(x)\nabla f_i(x)=2Df(x)^Tf(x) \end{aligned}\] となり、\(\hat{x}\)が\(\|f(x)\|^2\)を最小化するとは、\[2Df(\hat{x})^Tf(\hat{x})=0\](最適正条件(optimality condition))を満たすことである。
\(f\)がアフィン関数ならば、この最適正条件は線形最小二乗法の同条件(正規方程式)に帰着する。
18 Nonlinear least squares > 18.2 Gauss–Newton algorithm > 18.2.2 Newton algorithm (p.388)
\(n\)次元ベクトル\(\textbf{x}=(x_1,\dots,x_n)\)を変数とする、\(m\)本の非線形方程式。
\[f_i(x)=0,\quad i=1,\dots,m\]
ここで\(f_i:\textbf{R}^n\rightarrow \textbf{R}\)はスカラー方程式を意味する。
以下の線形スカラー方程式(\(n=m=1\))を例として、\(f(x)=0\)となる\(x\)を求める。
\[f(x)=\dfrac{e^x-e^{-x}}{e^x+e^{-x}},\quad f^{\prime}(x)=\dfrac{4e^{2x}}{(e^{2x}+1)^2}\]
f <- function(x) {
# (exp(x)-exp(-x))/(exp(x)+exp(-x))
tanh(x = x)
}
Df <- function(x) {
4 * exp(2 * x) / (exp(2 * x) + 1)^2
}
func_newton <- function(f, Df, x1, kmax = 5, tol = 1e-6) {
x <- fk <- vector()
x[1] <- x1
for (k in seq(kmax)) {
fk[k] <- f(x[k])
if (abs(fk[k]) < tol) {
break
}
x[k + 1] <- x[k] - fk[k] / Df(x[k])
}
return(list(x = x, fk = fk))
}
g <- ggplot(data = data.frame(x = c(-3, 3)), aes(x = x))
g <- g + stat_function(fun = f, mapping = aes(col = "f(x)"))
g <- g + stat_function(fun = Df, mapping = aes(col = "Df(x)"))
g <- g + theme(legend.title = element_blank()) + labs(y = "")
g + geom_hline(yintercept = 0)
# f(x)=0 となる x を求める。# 初期値を0.95として探索。
x1 <- 0.95
result <- func_newton(f = f, Df = Df, x1 = x1)
result$fk %>% plot(type = "o")
list(x = result$x, fk = result$fk)
# f(x)はゼロに収束していく。$x
[1] 0.9500000000000 -0.6840814557642 0.2343069290192 -0.0086702458951
[5] 0.0000004345197
$fk
[1] 0.7397830512740 -0.5941663642652 0.2301112455003 -0.0086700286450
[5] 0.000000434519718 Nonlinear least squares > 18.3 Levenberg–Marquardt algorithm (p.391)
ヤコビ行列
多変数ベクトル値函数\(f:\textbf{R}^n\rightarrow\textbf{R}^m\)のヤコビ行列\(\textbf{J}_f\)は以下の通り。 \[\textbf{J}_f=\dfrac{\partial f}{\partial x}=\begin{bmatrix} \dfrac{\partial f_1}{\partial x_1}&\cdots&\dfrac{\partial f_1}{\partial x_n}\\ \vdots&\ddots&\vdots\\ \dfrac{\partial f_m}{\partial x_1}&\cdots&\dfrac{\partial f_m}{\partial x_n}\\ \end{bmatrix},\quad f=\begin{bmatrix} f_1(x_1,\dots,x_n)\\ \vdots\\ f_m(x_1,\dots,x_n)\\ \end{bmatrix}\]
- 「一変数スカラー値関数における接線の傾き」および「一変数ベクトル値関数の勾配」の拡張、高次元化。
- ヤコビ行列の行列式は「ヤコビ行列式」あるいは「ヤコビアン」。
参考引用資料
ヘッセ行列
二階偏微分が存在する多変数スカラー値関数\(f(\textbf{x}),\quad\textbf{x}=(x_1,\dots,x_n)\)のヘッセ行列\(\textbf{H}(f)\)(\(n\times n\))は以下の通り。 \[\textbf{H}(f)= \begin{bmatrix} \dfrac{\partial^2f}{\partial x_1^2}&\dfrac{\partial^2f}{\partial x_1\partial x_2}&\cdots&\dfrac{\partial^2f}{\partial x_1\partial x_n}\\ \dfrac{\partial^2f}{\partial x_2\partial x_1}&\dfrac{\partial^2f}{\partial x_2^2}&\cdots&\dfrac{\partial^2f}{\partial x_2\partial x_n}\\ \vdots&\vdots&\ddots&\vdots\\ \dfrac{\partial^2f}{\partial x_n\partial x_1}&\dfrac{\partial^2f}{\partial x_n\partial x_2}&\cdots&\dfrac{\partial^2f}{\partial x_n^2}\\ \end{bmatrix}\]
- 多変数スカラー値関数の二階偏導関数全体が作る正方行列。
- ヘッセ行列の行列式は「ヘッシアン」。
- \(f\)が一変数関数の場合、ヘッセ行列は二階微分とおなじ。\(\textbf{H}(f)=f^{\prime\prime}(x)\)
- 偏微分の順に影響されないため、ヘッセ行列は対称行列となる。
参考引用資料
関数のテイラー展開
1変数の場合
\(x\simeq a\)のとき、\(f(x)\)のテイラー展開(ここでは2次近似式)は\[f(x)\simeq f(a)+f^{\prime}(a)(x-a)+\dfrac{f^{\prime\prime}(a)}{2}(x-a)^2\]
例として\(f(x)=x^5,\quad f^{\prime}(x)=5x^4,\quad f^{\prime\prime}(x)=20x^3\)の場合、
a <- -5
g <- ggplot(data = data.frame(x = seq(-10, 10, 0.1)), mapping = aes(x = x)) +
stat_function(fun = function(x) x^5) +
stat_function(
fun = function(x) a^5 + 5 * a^4 * (x - a) + 10 * a^3 * (x - a)^2,
mapping = aes(color = paste0("x = ", a, " での二次近似式"))
) +
xlim(c(-7.5, 0)) +
geom_vline(xintercept = a, linetype = "dashed") +
theme(legend.title = element_blank())
gまた上記2次近似式を\[f(x+\Delta x)\simeq f(x)+f^{\prime}(x)\Delta x+\dfrac{1}{2}f^{\prime\prime}(x)\Delta x^2\]と書き直し、\(\Delta x\)で微分した、\[f^{\prime}(x)+f^{\prime\prime}(x)\Delta x\]をゼロとすると、\(\Delta x=-\dfrac{f^{\prime}(x)}{f^{\prime\prime}(x)}\)
さらに\(\Delta x = x^{(k+1)}-x^{(k)}\)であるため、\[x^{(k+1)}=x^{(k)}-\dfrac{f^{\prime}(x)}{f^{\prime\prime}(x)}\]となり、極値は
多変数の場合
\(f(x_1,\dots,x_n)\)のテイラー展開(ここでは2次近似式)は \[f(x_1+\Delta x_1,\dots,x_n+\Delta x_n)\simeq f(x_1,\dots,x_n)+ \displaystyle\sum_{i=1}^n \dfrac{\partial f(x_1,\dots,x_n)}{\partial x_i} \Delta x_i+ \dfrac{1}{2!}\displaystyle\sum_{i,j=1}^n\dfrac{\partial^2 f(x_1,\dots,x_n)}{\partial x_i \partial x_j}\Delta x_i\Delta x_j\]
\(\Delta x_i\)で微分したものをゼロとおくと(近似式の極値を求める)、右辺第一項は消え、同第二項は勾配(一階偏微分)、そして同第三項はヘッセ行列(二階偏微分)となる。 \[\begin{bmatrix}\dfrac{\partial f(x_1,\dots,x_n)}{\partial x_1}\\\vdots\\\dfrac{\partial f(x_1,\dots,x_n)}{\partial x_n}\end{bmatrix}+ \begin{bmatrix} \dfrac{\partial^2f(x_1,\dots,x_n)}{\partial x_1^2}&\cdots&\dfrac{\partial^2f(x_1,\dots,x_n)}{\partial x_1\partial x_n}\\ \vdots&\ddots&\vdots\\ \dfrac{\partial^2f(x_1,\dots,x_n)}{\partial x_n\partial x_1}&\cdots&\dfrac{\partial^2f(x_1,\dots,x_n)}{\partial x_n^2}\\ \end{bmatrix}\Delta \textbf{x}=\nabla f+\textbf{H}\Delta \textbf{x}=\textbf{0}\]
\(\Delta \textbf{x} = \textbf{x}^{(k+1)}-\textbf{x}^{(k)}\)であるため、 \[\begin{aligned} \Delta \textbf{x}=-\textbf{H}^{-1}\nabla f\\ \textbf{x}^{(k+1)}=\textbf{x}^{(k)}-\textbf{H}^{-1}\nabla f \end{aligned}\]
なお、このヘッセ行列を利用して\(\Delta \textbf{x}\)を求め、\(\textbf{x}\)を更新していくのがニュートン法。
ガウス・ニュートン法
対象関数を次の非線形自乗和(ガウス・ニュートン法の前提)とする。 \[f(\textbf{x})=\displaystyle\sum_{i=1}^m r_i^2(\textbf{x}),\quad \textbf{x}=(x_1,\dots,x_n)\]
\(f\)の一階偏微分は次の通り(\(x_k\)で偏微分した場合)。 \[\dfrac{\partial f}{\partial x_k}=\dfrac{\partial }{\partial x_k}\displaystyle\sum_{i=1}^mr_i^2=\displaystyle\sum_{i=1}^m 2r_i\dfrac{\partial r_i}{\partial x_k}=2\displaystyle\sum_{i=1}^m r_i\dfrac{\partial r_i}{\partial x_k}\]
一般化すると\[\dfrac{\partial f}{\partial x}=\nabla f(x)=2\textbf{J}^T\textbf{r}\]
さらにその偏微分(\(f\)の二階偏微分、つまりヘッセ行列)は偏微分の積の公式より次の通り(\(x_l\)で偏微分した場合)。 \[\dfrac{\partial }{\partial x_l} \left(2\displaystyle\sum_{i=1}^m r_i\dfrac{\partial r_i}{\partial x_k}\right)=2\displaystyle\sum_{i=1}^m\dfrac{\partial r_i}{\partial x_l}\dfrac{\partial r_i}{\partial x_k}+2\displaystyle\sum_{i=1}^m r_i\dfrac{\partial^2 r_i}{\partial x_k\partial x_l}=\textbf{H}_{lk}\]
- 偏微分の積の公式
\[\dfrac{\partial}{\partial x}\left(f(x,y)\,\,g(x,y)\right)=\left(\dfrac{\partial}{\partial x}f(x,y)\right)g(x,y)+f(x,y)\left(\dfrac{\partial}{\partial x}g(x,y)\right)\] ここで、右辺第二項を無視して(\(\beta\)が解に近い場合\(r_i\)は小さくなる)、ヘッセ行列を以下の通りに近似する。 \[\textbf{H}_{lk}\simeq 2\displaystyle\sum_{i=1}^m\dfrac{\partial r_i}{\partial x_l}\dfrac{\partial r_i}{\partial x_k}=2\displaystyle\sum_{i=1}^m \textbf{J}_{il}\textbf{J}_{ik}\]
一般化すると\[\textbf{H}\simeq2\textbf{J}^T\textbf{J}\]
その上で前述のニュートン法\[\textbf{x}^{(k+1)}=\textbf{x}^{(k)}-\textbf{H}^{-1}\nabla f\]に一般化したヘッセ行列とヤコビ行列を代入して、 \[x^{(k+1)}=x^{(k)}-\left(2\textbf{J}^T\textbf{J}\right)^{-1}\cdot 2\textbf{J}^T\textbf{r} = x^{(k)}-1/2\left(\textbf{J}^T\textbf{J}\right)^{-1}\cdot 2\textbf{J}^T\textbf{r} = x^{(k)}-\left(\textbf{J}^T\textbf{J}\right)^{-1}\cdot \textbf{J}^T\textbf{r}\]
とし、\(\Delta \textbf{x}\)を更新していくのがガウス・ニュートン法。
つまり計算コストの高いヘッセ行列の逆行列算出を避けで同近似を利用するのがガウス・ニュートン法となる。
- よって、右辺第一項が同第二項より非常に小さい場合のみ、収束が保証される。
なお、右辺第二項は正規方程式に他ならない。
但し\(\textbf{J}^T\textbf{J}\)が正定値でないと近似が凸関数とはならないため、更新の方向が減少に向かわない。
そこで右辺第二項の第一因子に罰則項\(\lambda \textbf{I}\)を加算するのがレーベンバーグ・マーカート法\((\lambda>0)\)。 \[x^{(k+1)} = x^{(k)}-\left(\textbf{J}^T\textbf{J}+\lambda \textbf{I}\right)^{-1}\cdot \textbf{J}^T\textbf{r}\]
レーベンバーグ・マーカート法では、一つ前の\[f(x^{(k)})\]のノルムより更新後の\[f(x^{(k+1)})\]のノルムのほうが小さい場合、つまり誤差が小さくなった場合は\(\lambda\)を小さくして\(λ\textbf{I}\)の寄与を小さくして(=ガウスニュートン法に近づく)、\(x\)を更新。\[x^{(k+1)} = x^{(k)}-\left(\textbf{J}^T\textbf{J}\right)^{-1}\cdot \textbf{J}^T\textbf{r}\]
また誤差が大きくなってしまった場合は\(λ\)を大きくしてヤコビアン行列の積の寄与小さくし(=最急降下法に近づく)、\(x\)は更新しない。 \[x^{(k+1)} = x^{(k)}- \textbf{J}^T\textbf{r}\]
なお、\(\|\textbf{A}x-\textbf{B}\|\)として、最小自乗法により\(\Delta x\)を求める場合の\(\textbf{A},\textbf{B}\)は次の通り。 \[\textbf{A}=\begin{bmatrix} \dfrac{\partial r_1}{\partial \beta_1}&\dfrac{\partial r_1}{\partial \beta_2}\\ \vdots&\vdots\\ \dfrac{\partial r_7}{\partial \beta_1}&\dfrac{\partial r_7}{\partial \beta_2}\\ \sqrt{\lambda}&0\\ 0&\sqrt{\lambda}\\ \end{bmatrix},\quad \textbf{B}=\begin{bmatrix}r_1\\\vdots\\r_7\\0\\0\end{bmatrix}\]
参考引用資料
- http://www.core.kochi-tech.ac.jp/m_inoue/work/pdf/2010/syokyu02/46.pdf
- https://lecture.ecc.u-tokyo.ac.jp/~nkiyono/kiyono/16_6-06.pdf
- https://lecture.ecc.u-tokyo.ac.jp/~nkiyono/kiyono/12_6-08.pdf
- http://www.dais.is.tohoku.ac.jp/~shioura/teaching/mp04/mp04-8.pdf
- https://ja.wikipedia.org/wiki/%E3%82%AC%E3%82%A6%E3%82%B9%E3%83%BB%E3%83%8B%E3%83%A5%E3%83%BC%E3%83%88%E3%83%B3%E6%B3%95
- https://www2.math.kyushu-u.ac.jp/~snii/Calculus/2.pdf
- http://www.cse.iitm.ac.in/~vplab/courses/optimization/Optim_methods.pdf
- http://tcu-yoshida-lab.org/Inverse_HP/pdf_ss/1_6_masumoto.pdf
- https://w3e.kanazawa-it.ac.jp/math/category/bibun/henbibun/henkan-tex.cgi?target=/math/category/bibun/henbibun/henbibun-kosiki.html
f <- function(beta, x, y) {
r <- y - beta[1] * x / (beta[2] + x) %>% matrix(ncol = 1)
return(r)
}
Df <- function(beta, x) {
J <- cbind(-x / (beta[2] + x), beta[1] * x / (beta[2] + x)^2)
# 第1列は beta[1] での r の偏微分、第2列は beta[2] での r の偏微分とするヤコビ行列。
return(J)
}
lsm <- function(A, B) {
QR <- qr(x = A)
Q <- qr.Q(QR)
R <- qr.R(QR)
b <- t(Q) %*% B
beta_hat <- solve(a = R) %*% b
return(beta_hat)
}
levenberg_marquardt <- function(beta, x, y, lambda, n) {
fk <- f(beta = beta, x = x, y = y)
Dfk <- Df(beta = beta, x = x)
beta_hat <- solve(t(Dfk) %*% Dfk + lambda * diag(1, n)) %*% (t(Dfk) %*% fk)
# または
A <- rbind(Dfk, sqrt(lambda) * diag(x = 1, nrow = n))
B <- rbind(fk, diag(x = 0, nrow = n, ncol = 1))
beta_hat_by_lsm <- lsm(A = A, B = B)
beta <- beta - beta_hat
# 一つ前との比較
if (f(beta = beta, x = x, y = y) %>% norm(type = "2") < norm(fk, type = "2")) {
# 残差が小さくなった場合
lambda <- 0.8 * lambda
} else {
# 残差が小さくなっていない場合
lambda <- 2.0 * lambda
}
# 目的関数 = 残差の自乗和
objective <- norm(fk, type = "2")^2
# 最適正条件(||f(x)||^2の最小化)の確認
residual <-
{
2 * t(Dfk) %*% fk
} %>% norm(type = "2")
return(list(
beta = beta, beta_hat = beta_hat, beta_hat_by_lsm = beta_hat_by_lsm,
objective = objective, residual = residual, lambda = lambda,
fk = fk, Dfk = Dfk, A = A, B = B
))
}
func_plot <- function(g, beta, iterate) {
g <- g + stat_function(fun = function(x) beta[1] * x / (beta[2] + x), color = "red") +
labs(title = paste0("k = ", iterate))
return(g)
}# サンプル
gg <- list()
x <- c(0.038, 0.194, 0.425, 0.626, 1.253, 2.500, 3.740)
y <- c(0.050, 0.127, 0.094, 0.2122, 0.2729, 0.2665, 0.3317)
g <- ggplot(data = data.frame(x = x, y = y)) +
geom_point(mapping = aes(x = x, y = y))
g# 初期値
iterate <- 0
beta_0 <- c(0.9, 0.2) %>% matrix(ncol = 1)
gg[[iterate + 1]] <- func_plot(g = g, beta = beta_0, iterate = iterate)# 1周目
n <- length(beta_0)
lambda_0 <- 1
iterate <- iterate + 1
result <- levenberg_marquardt(beta = beta_0, x = x, y = y, lambda = lambda_0, n = n)
result
beta_1 <- result$beta
lambda_1 <- result$lambda
gg[[iterate + 1]] <- func_plot(g = g, beta = beta_1, iterate = iterate)$beta
[,1]
[1,] 0.5080249
[2,] 0.3553962
$beta_hat
[,1]
[1,] 0.3919751
[2,] -0.1553962
$beta_hat_by_lsm
[,1]
[1,] 0.3919751
[2,] -0.1553962
$objective
[1] 1.445497
$residual
[1] 5.974309
$lambda
[1] 0.8
$fk
[,1]
[1,] -0.09369748
[2,] -0.31614721
[3,] -0.51800000
[4,] -0.46988232
[5,] -0.50321838
[6,] -0.56683333
[7,] -0.52261472
$Dfk
[,1] [,2]
[1,] -0.1596639 0.6037709
[2,] -0.4923858 1.1247391
[3,] -0.6800000 0.9792000
[4,] -0.7578692 0.8257655
[5,] -0.8623538 0.5341489
[6,] -0.9259259 0.3086420
[7,] -0.9492386 0.2168311
$A
[,1] [,2]
[1,] -0.1596639 0.6037709
[2,] -0.4923858 1.1247391
[3,] -0.6800000 0.9792000
[4,] -0.7578692 0.8257655
[5,] -0.8623538 0.5341489
[6,] -0.9259259 0.3086420
[7,] -0.9492386 0.2168311
[8,] 1.0000000 0.0000000
[9,] 0.0000000 1.0000000
$B
[,1]
[1,] -0.09369748
[2,] -0.31614721
[3,] -0.51800000
[4,] -0.46988232
[5,] -0.50321838
[6,] -0.56683333
[7,] -0.52261472
[8,] 0.00000000
[9,] 0.00000000# 2周目
iterate <- iterate + 1
result <- levenberg_marquardt(beta = beta_1, x = x, y = y, lambda = lambda_1, n = n)
result
beta_2 <- result$beta
lambda_2 <- result$lambda
gg[[iterate + 1]] <- func_plot(g = g, beta = beta_2, iterate = iterate)$beta
[,1]
[1,] 0.3745055
[2,] 0.4057333
$beta_hat
[,1]
[1,] 0.13351944
[2,] -0.05033713
$beta_hat_by_lsm
[,1]
[1,] 0.13351944
[2,] -0.05033713
$objective
[1] 0.112997
$residual
[1] 1.187239
$lambda
[1] 0.64
$fk
[,1]
[1,] 0.0009274647
[2,] -0.0523911985
[3,] -0.1826679365
[4,] -0.1118522232
[5,] -0.1228701838
[6,] -0.1782937422
[7,] -0.1322388218
$Dfk
[,1] [,2]
[1,] -0.09659474 0.1247408
[2,] -0.35311494 0.3265243
[3,] -0.54459519 0.3545224
[4,] -0.63786676 0.3301951
[5,] -0.77903692 0.2460651
[6,] -0.87553525 0.1557730
[7,] -0.91322056 0.1132830
$A
[,1] [,2]
[1,] -0.09659474 0.1247408
[2,] -0.35311494 0.3265243
[3,] -0.54459519 0.3545224
[4,] -0.63786676 0.3301951
[5,] -0.77903692 0.2460651
[6,] -0.87553525 0.1557730
[7,] -0.91322056 0.1132830
[8,] 0.89442719 0.0000000
[9,] 0.00000000 0.8944272
$B
[,1]
[1,] 0.0009274647
[2,] -0.0523911985
[3,] -0.1826679365
[4,] -0.1118522232
[5,] -0.1228701838
[6,] -0.1782937422
[7,] -0.1322388218
[8,] 0.0000000000
[9,] 0.0000000000# 3周目
iterate <- iterate + 1
result <- levenberg_marquardt(beta = beta_2, x = x, y = y, lambda = lambda_2, n = n)
result
beta_3 <- result$beta
lambda_3 <- result$lambda
gg[[iterate + 1]] <- func_plot(g = g, beta = beta_3, iterate = iterate)$beta
[,1]
[1,] 0.3439373
[2,] 0.4209832
$beta_hat
[,1]
[1,] 0.03056823
[2,] -0.01524985
$beta_hat_by_lsm
[,1]
[1,] 0.03056823
[2,] -0.01524985
$objective
[1] 0.01334826
$residual
[1] 0.2417889
$lambda
[1] 0.512
$fk
[,1]
[1,] 0.017928463
[2,] 0.005856041
[3,] -0.097595589
[4,] -0.015029693
[5,] -0.009999842
[6,] -0.055712553
[7,] -0.006153514
$Dfk
[,1] [,2]
[1,] -0.08563702 0.07227660
[2,] -0.32347712 0.20199638
[3,] -0.51159620 0.23063429
[4,] -0.60674594 0.22024073
[5,] -0.75539570 0.17055173
[6,] -0.86036802 0.11088855
[7,] -0.90213232 0.08149427
$A
[,1] [,2]
[1,] -0.08563702 0.07227660
[2,] -0.32347712 0.20199638
[3,] -0.51159620 0.23063429
[4,] -0.60674594 0.22024073
[5,] -0.75539570 0.17055173
[6,] -0.86036802 0.11088855
[7,] -0.90213232 0.08149427
[8,] 0.80000000 0.00000000
[9,] 0.00000000 0.80000000
$B
[,1]
[1,] 0.017928463
[2,] 0.005856041
[3,] -0.097595589
[4,] -0.015029693
[5,] -0.009999842
[6,] -0.055712553
[7,] -0.006153514
[8,] 0.000000000
[9,] 0.000000000# 4周目
iterate <- iterate + 1
result <- levenberg_marquardt(beta = beta_3, x = x, y = y, lambda = lambda_3, n = n)
result
beta_4 <- result$beta
lambda_4 <- result$lambda
gg[[iterate + 1]] <- func_plot(g = g, beta = beta_4, iterate = iterate)$beta
[,1]
[1,] 0.3395347
[2,] 0.4307968
$beta_hat
[,1]
[1,] 0.004402532
[2,] -0.009813624
$beta_hat_by_lsm
[,1]
[1,] 0.004402532
[2,] -0.009813624
$objective
[1] 0.008580304
$residual
[1] 0.04390834
$lambda
[1] 0.4096
$fk
[,1]
[1,] 0.021524845
[2,] 0.018502994
[3,] -0.078785168
[4,] 0.006557023
[5,] 0.015458100
[6,] -0.027867731
[7,] 0.022560224
$Dfk
[,1] [,2]
[1,] -0.08279171 0.06203965
[2,] -0.31545580 0.17642273
[3,] -0.50237407 0.20424185
[4,] -0.59790838 0.19641479
[5,] -0.74851410 0.15379002
[6,] -0.85587621 0.10077694
[7,] -0.89882604 0.07429489
$A
[,1] [,2]
[1,] -0.08279171 0.06203965
[2,] -0.31545580 0.17642273
[3,] -0.50237407 0.20424185
[4,] -0.59790838 0.19641479
[5,] -0.74851410 0.15379002
[6,] -0.85587621 0.10077694
[7,] -0.89882604 0.07429489
[8,] 0.71554175 0.00000000
[9,] 0.00000000 0.71554175
$B
[,1]
[1,] 0.021524845
[2,] 0.018502994
[3,] -0.078785168
[4,] 0.006557023
[5,] 0.015458100
[6,] -0.027867731
[7,] 0.022560224
[8,] 0.000000000
[9,] 0.000000000# 5周目
iterate <- iterate + 1
result <- levenberg_marquardt(beta = beta_4, x = x, y = y, lambda = lambda_4, n = n)
result
beta_5 <- result$beta
lambda_5 <- result$lambda
gg[[iterate + 1]] <- func_plot(g = g, beta = beta_5, iterate = iterate)$beta
[,1]
[1,] 0.3404461
[2,] 0.4405002
$beta_hat
[,1]
[1,] -0.000911315
[2,] -0.009703416
$beta_hat_by_lsm
[,1]
[1,] -0.000911315
[2,] -0.009703416
$objective
[1] 0.008347155
$residual
[1] 0.01075202
$lambda
[1] 0.32768
$fk
[,1]
[1,] 0.02247780
[2,] 0.02157414
[3,] -0.07461744
[4,] 0.01107453
[5,] 0.02023469
[6,] -0.02312665
[7,] 0.02723541
$Dfk
[,1] [,2]
[1,] -0.08105858 0.05870817
[2,] -0.31050096 0.16873625
[3,] -0.49661323 0.19702977
[4,] -0.59235608 0.19031613
[5,] -0.74415156 0.15005689
[6,] -0.85301036 0.09882181
[7,] -0.89671116 0.07299914
$A
[,1] [,2]
[1,] -0.08105858 0.05870817
[2,] -0.31050096 0.16873625
[3,] -0.49661323 0.19702977
[4,] -0.59235608 0.19031613
[5,] -0.74415156 0.15005689
[6,] -0.85301036 0.09882181
[7,] -0.89671116 0.07299914
[8,] 0.64000000 0.00000000
[9,] 0.00000000 0.64000000
$B
[,1]
[1,] 0.02247780
[2,] 0.02157414
[3,] -0.07461744
[4,] 0.01107453
[5,] 0.02023469
[6,] -0.02312665
[7,] 0.02723541
[8,] 0.00000000
[9,] 0.0000000018 Nonlinear least squares > 18.3.1 Examples (p.394)
Equilibrium prices. (p.394)
需要弾性値行列(demand supply elasticity matrx)を\(E^{\textrm{d}}\)、供給弾性値行列(suppl supply elasticity matrx)を\(E^{\textrm{s}}\)、名目需要ベクトル(nominal demand vector)を\(d^{\textrm{nom}}\)、名目供給ベクトル(nominal supply vector)を\(s^{\textrm{nom}}\)、需要関数を\[D(p)=\textrm{exp}\left(\textbf{E}^\textrm{d}\,\textrm{log}\,p+d^{\textrm{nom}}\right)\]、供給関数を\[S(p)=\textrm{exp}\left(\textbf{E}^\textrm{s}\,\textrm{log}\,p+s^{\textrm{nom}}\right)\]として、超過供給がゼロ \[f(p)=S(p)-D(p)=0\]となる2つの価格(\(p_1,p_2\))を探索する。
また\(f(x)\)の微分は以下の通り。 \[Df(x)=\begin{bmatrix} \dfrac{x_1-(a_1)_1}{\|x-a_1\|}&\dfrac{x_2-(a_1)_2}{\|x-a_1\|}\\ \vdots&\vdots\\ \dfrac{x_1-(a_m)_1}{\|x-a_m\|}&\dfrac{x_2-(a_m)_2}{\|x-a_m\|} \end{bmatrix}\]
snom <- c(2.2, 0.3)
dnom <- c(3.1, 2.2)
Es <- matrix(data = c(0.5, -.3, -.15, .8), nrow = 2, byrow = T)
Ed <- matrix(data = c(-0.5, 0.2, -0.0, -0.5), nrow = 2, byrow = T)
func_S <- function(Es, p, snom) {
exp(Es %*% log(p) %>% t() + snom)
}
func_D <- function(Ed, p, dnom) {
exp(Ed %*% log(p) %>% t() + dnom)
}
f <- function(p, Es, Ed, snom, dnom) {
p <- t(p)
t(func_S(Es = Es, p = p, snom = snom) - func_D(Ed = Ed, p = p, dnom = dnom))
}
Df <- function(p, Es, Ed, snom, dnom) {
p <- t(p)
S <- func_S(Es = Es, p = p, snom = snom)
D <- func_D(Ed = Ed, p = p, dnom = dnom)
a <- rbind(cbind(S[1] * Es[1, 1] / p[1], S[1] * Es[1, 2] / p[2]), cbind(S[2] * Es[2, 1] / p[1], S[2] * Es[2, 2] / p[2]))
b <- rbind(cbind(D[1] * Ed[1, 1] / p[1], D[1] * Ed[1, 2] / p[2]), cbind(D[2] * Ed[2, 1] / p[1], D[2] * Ed[2, 2] / p[2]))
a - b
}
func_levenberg_marquardt <- function(f, Df, x1, lambda1, kmax = 100, tol = 1e-6) {
n <- length(x1)
lambd <- traject_lambd <- lambda1
objectives <- residuals <- vector()
x <- traject_x <- t(x1)
for (k in seq(kmax)) {
fk <- f(p = t(x), Es = Es, Ed = Ed, snom = snom, dnom = dnom)
Dfk <- Df(p = t(x), Es = Es, Ed = Ed, snom = snom, dnom = dnom)
objectives[k] <- norm(fk, type = "2")^2
residuals[k] <- norm(
{
t(Dfk) %*% fk
} %>%
{
. * 2
},
type = "2"
)
if (norm(
{
t(Dfk) %*% fk
} * 2,
type = "2"
) < tol) {
break
}
A <- rbind(Dfk, sqrt(lambd) * diag(x = 1, nrow = n))
y <- rbind(fk, diag(x = 0, nrow = n, ncol = 1))
QR <- qr(x = A)
Q <- qr.Q(QR)
R <- qr.R(QR)
b <- t(Q) %*% y
x_hat <- solve(a = R) %*% b
xt <- x - x_hat
if (f(p = t(xt), Es = Es, Ed = Ed, snom = snom, dnom = dnom) %>% norm(type = "2") < norm(fk, type = "2")) {
lambd <- 0.8 * lambd
x <- xt
} else {
lambd <- 2.0 * lambd
}
traject_lambd <- c(traject_lambd, lambd)
traject_x <- cbind(traject_x, x)
}
list(x = x, objectives = objectives, residuals = residuals, traject_x = traject_x, traject_lambd = traject_lambd)
}# xの初期値(x1)をp1=3、p2=10とする。
lambda1 <- 1
x1 <- matrix(c(3, 9), ncol = 2)
result <- func_levenberg_marquardt(f = f, Df = Df, x1 = x1, lambda1 = lambda1)
traject_x <- result$traject_x %>%
t() %>%
data.frame()
ggplot(data = traject_x, mapping = aes(x = X1, y = X2)) +
geom_path(arrow = arrow(ends = "last")) +
geom_point() +
scale_x_continuous(breaks = pretty_breaks(n = 10), limits = c(2, 10)) +
scale_y_continuous(breaks = pretty_breaks(n = 5), limits = c(2, 10)) +
coord_fixed() +
labs(x = "p1", y = "p2")
traject_x X1 X2
1 3.000000 9.000000
2 5.218607 7.447162
3 6.051393 6.312320
4 5.949433 5.780217
5 5.792178 5.502769
6 5.704126 5.361188
7 5.664950 5.298901
8 5.650301 5.275616
9 5.645672 5.268248
10 5.644441 5.266286
11 5.644168 5.265849
12 5.644117 5.265769
13 5.644109 5.265756
14 5.644109 5.265755objectives <- result$objectives
data.frame(k = seq(objectives), `||f(p(k))||^2` = objectives, check.names = F) %>%
ggplot(mapping = aes(x = .[, 1], y = .[, 2])) +
geom_line() +
geom_point() +
labs(x = "k", y = "||f(p(k))||^2")Location from range measurements. (p.396)
func_dist <- function(x) {
((x[1, 1] - A[, 1])^2 + (x[2, 1] - A[, 2])^2) %>% sqrt()
}
f <- function(x) {
func_dist(x) %>% matrix(ncol = 1) - t(rhos)
}
Df <- function(x) {
diag(x = 1 / func_dist(x)) %*% t(rbind(x[1, 1] - A[, 1], x[2, 1] - A[, 2]))
}
func_lsm <- function(A, y) {
QR <- qr(x = A)
Q <- qr.Q(QR)
R <- qr.R(QR)
b <- t(Q) %*% y
x_hat <- solve(a = R) %*% b
return(x_hat)
}
func_levenberg_marquardt <- function(f, Df, x1, lambda1, kmax = 100, tol = 1e-6) {
n <- length(x1)
lambd <- traject_lambd <- lambda1
objectives <- residuals <- vector()
x <- traject_x <- x1
for (k in seq(kmax)) {
fk <- f(x = x)
Dfk <- Df(x = x)
objectives[k] <- norm(fk, type = "2")^2
residuals[k] <- norm(
{
t(Dfk) %*% fk
} %>%
{
. * 2
},
type = "2"
)
if (norm(
{
t(Dfk) %*% fk
} * 2,
type = "2"
) < tol) {
break
}
x_hat <- func_lsm(
A = rbind(Dfk, sqrt(lambd) * diag(x = 1, nrow = n)),
y = rbind(fk, diag(x = 0, nrow = n, ncol = 1))
)
xt <- x - x_hat
if (f(x = xt) %>% norm(type = "2") < norm(fk, type = "2")) {
lambd <- 0.8 * lambd
x <- xt
} else {
lambd <- 2.0 * lambd
}
traject_lambd <- c(traject_lambd, lambd)
traject_x <- cbind(traject_x, x)
}
list(x = x, objectives = objectives, residuals = residuals, traject_x = traject_x, traject_lambd = traject_lambd)
}A <- c(1.8, 2.5, 2.0, 1.7, 1.5, 1.5, 1.5, 2.0, 2.5, 1.5) %>% matrix(ncol = 2, byrow = T)
rhos <- c(1.87288, 1.23950, 0.53672, 1.29273, 1.49353) %>% matrix(nrow = 1)
lambda1 <- 0.1
objective <- lambda <- traject_x <- list()
for (iii in 1:3) {
x1 <- switch(iii,
"1" = c(1.8, 3.5),
"2" = c(3.0, 1.5),
"3" = c(2.2, 3.5)
) %>% matrix(ncol = 1)
result <- func_levenberg_marquardt(f = f, Df = Df, x1 = x1, lambda1 = lambda1)
o <- result$objectives
l <- result$traject_lambd
objective[[iii]] <- data.frame(k = seq(o), v = o, s = paste0("x1=", paste0(x1, collapse = ",")))
lambda[[iii]] <- data.frame(k = seq(l), v = l, s = paste0("x1=", paste0(x1, collapse = ",")))
traject_x[[iii]] <- result$traject_x
}xrange <- sapply(objective, function(x) nrow(x)) %>%
min() %>%
c(0, .)
Reduce(function(x, y) rbind(x, y), objective) %>% ggplot(mapping = aes(x = k, y = v, col = s)) +
geom_line() +
geom_point() +
scale_x_continuous(breaks = pretty_breaks(10), limits = xrange) +
theme(legend.title = element_blank()) +
labs(y = "||f(x^(k))||^2")xrange <- sapply(lambda, function(x) nrow(x)) %>%
min() %>%
c(0, .)
Reduce(function(x, y) rbind(x, y), lambda) %>% ggplot(mapping = aes(x = k, y = v, col = s)) +
geom_line() +
geom_point() +
scale_x_continuous(breaks = pretty_breaks(10), limits = xrange) +
theme(legend.title = element_blank()) +
labs(y = "λ^(k)")g <- ggplot()
g <- g +
geom_path(
mapping = aes(x = traject_x[[1]][1, ], y = traject_x[[1]][2, ], color = "x1=1.8,3.5"),
arrow = arrow(ends = "last")
) +
geom_point(mapping = aes(x = traject_x[[1]][1, ], y = traject_x[[1]][2, ], color = "x1=1.8,3.5"))
g <- g +
geom_path(
mapping = aes(x = traject_x[[2]][1, ], y = traject_x[[2]][2, ], color = "x1=3.0,1.5"),
arrow = arrow(ends = "last")
) +
geom_point(mapping = aes(x = traject_x[[2]][1, ], y = traject_x[[2]][2, ], color = "x1=3.0,1.5"))
g <- g +
geom_path(
mapping = aes(x = traject_x[[3]][1, ], y = traject_x[[3]][2, ], color = "x1=2.2,3.5"),
arrow = arrow(ends = "last")
) +
geom_point(mapping = aes(x = traject_x[[3]][1, ], y = traject_x[[3]][2, ], color = "x1=2.2,3.5"))
g <- g + geom_point(mapping = aes(x = A[, 1], y = A[, 2]))
g + scale_x_continuous(breaks = pretty_breaks(n = 4), limits = c(0, 4)) +
scale_y_continuous(breaks = pretty_breaks(n = 4), limits = c(0, 4)) + coord_fixed() + labs(x = "x1", y = "x2") +
theme(legend.title = element_blank(), legend.position = "top")18 Nonlinear least squares > 18.4 Nonlinear model fitting (p.399)
Example. (p.399)
指数関数的に減衰するシグモイド関数(exponentially decaying sinusoid)を例とする。
\[\hat{f}(x;\theta)=\theta_1e^{\theta_2x}\textrm{cos}(\theta_3x+\theta_4)\]
library(latex2exp)
# サンプルデータ
theta_x <- c(1, -0.2, 2 * pi / 5, pi / 3) %>% matrix(nrow = 1)
M <- 30
xd <- c(5 * runif(n = M), 5 + 15 * runif(n = M)) %>% matrix(ncol = 1)
yd0 <- theta_x[1] * exp(theta_x[2] * xd) * cos(theta_x[3] * xd + theta_x[4])
N <- length(yd0)
# 各ポイント(n=60)に摂動を加算
yd <- t(yd0) * ((1 + 0.2 * rnorm(n = N)) + 0.015 * rnorm(n = N))
ggplot(mapping = aes(x = xd)) +
geom_point(mapping = aes(y = t(yd))) +
geom_point(mapping = aes(y = yd0), color = "red")f <- function(theta) {
t(t(theta[1] * exp(theta[2] * xd) * cos(theta[3] * xd + theta[4])) - yd)
}
Df <- function(theta) {
cbind(
exp(theta[2] * xd) * cos(theta[3] * xd + theta[4]),
theta[1] * (xd * exp(theta[2] * xd) * cos(theta[3] * xd + theta[4])),
-theta[1] * exp(theta[2] * xd) * xd * sin(theta[3] * xd + theta[4]),
-theta[1] * exp(theta[2] * xd) * sin(theta[3] * xd + theta[4])
)
}
func_lsm <- function(A, y) {
QR <- qr(x = A)
Q <- qr.Q(QR)
R <- qr.R(QR)
b <- t(Q) %*% y
x_hat <- solve(a = R) %*% b
return(x_hat)
}
func_levenberg_marquardt <- function(f, Df, x1, lambda1, kmax = 100, tol = 1e-6) {
n <- length(x1)
lambd <- traject_lambd <- lambda1
objectives <- residuals <- vector()
fk <- Dfk <- list()
x <- traject_x <- x1
for (k in seq(kmax)) {
fk[[k]] <- f(x)
Dfk[[k]] <- Df(x)
objectives[k] <- norm(fk[[k]], type = "2")^2
residuals[k] <- norm(
{
t(Dfk[[k]]) %*% fk[[k]]
} %>%
{
. * 2
},
type = "2"
)
if (norm(
{
t(Dfk[[k]]) %*% fk[[k]]
} * 2,
type = "2"
) < tol) {
break
}
x_hat <- func_lsm(
A = rbind(Dfk[[k]], sqrt(lambd) * diag(x = 1, nrow = n)),
y = rbind(fk[[k]], diag(x = 0, nrow = n, ncol = 1))
)
xt <- x - t(x_hat)
if (f(xt) %>% norm(type = "2") < norm(fk[[k]], type = "2")) {
lambd <- 0.8 * lambd
x <- xt
} else {
lambd <- 2.0 * lambd
}
traject_lambd <- c(traject_lambd, lambd)
traject_x <- rbind(traject_x, x)
}
list(
x = x, objectives = objectives, residuals = residuals, traject_x = traject_x,
traject_lambd = traject_lambd, fk = fk, Dfk = Dfk
)
}theta1 <- c(1, 0, 1, 0) %>% matrix(nrow = 1)
result <- func_levenberg_marquardt(f = f, Df = Df, x1 = theta1, lambda1 = 1)
theta <- result$x
x <- seq(0, 20, length.out = 500)
y <- theta[1] * exp(theta[2] * x) * cos(theta[3] * x + theta[4])
ggplot() +
geom_point(mapping = aes(x = xd, y = t(yd))) +
geom_line(mapping = aes(x = x, y = y), color = "red") +
labs(x = "x", y = TeX(input = "$\\hat{f}(x;\\theta)$")) +
theme(axis.title.y = element_text(angle = 0, vjust = 0.5))
result$traject_x [,1] [,2] [,3] [,4]
[1,] 1.00000000 0.0000000 1.0000000 0.0000000
[2,] 0.02533886 -0.0127977 0.9507923 0.5970111
[3,] 0.10148484 -0.2561487 1.2859479 0.8580388
[4,] 0.10148484 -0.2561487 1.2859479 0.8580388
[5,] 0.94769757 -0.0348284 1.3254557 0.9305408
[6,] 0.87576367 -0.1013714 1.3143572 0.9433692
[7,] 1.00220559 -0.1747747 1.2873739 0.9833818
[8,] 1.07957822 -0.2027316 1.2635516 1.0137931
[9,] 1.09951337 -0.2064800 1.2591542 1.0192364
[10,] 1.10455267 -0.2076083 1.2590578 1.0188676
[11,] 1.10577535 -0.2078858 1.2591187 1.0185340
[12,] 1.10603452 -0.2079440 1.2591384 1.0184415
[13,] 1.10608065 -0.2079542 1.2591424 1.0184235
[14,] 1.10608741 -0.2079557 1.2591430 1.0184207
[15,] 1.10608822 -0.2079559 1.2591430 1.0184204Orthogonal distance regression. (p.400)
\[\hat{f}(x;\theta)=\theta_1f_1(x)+\cdots+\theta_pf_p(x)\]
# サンプルデータ
list(xd = dim(xd), yd = dim(yd))
ggplot() +
geom_point(mapping = aes(x = xd, y = yd))$xd
[1] 25 1
$yd
[1] 25 1N <- length(xd)
p <- 4
A <- outer(X = as.vector(xd), Y = seq(p) - 1, FUN = "^")head(A) [,1] [,2] [,3] [,4]
[1,] 1 0.8638631 0.74625944 0.644665984
[2,] 1 0.9061876 0.82117604 0.744139577
[3,] 1 0.2001483 0.04005933 0.008017804
[4,] 1 0.8593952 0.73856018 0.634715102
[5,] 1 0.7959556 0.63354527 0.504273886
[6,] 1 0.3381977 0.11437770 0.038682280tail(A) [,1] [,2] [,3] [,4]
[20,] 1 0.8655181 0.7491216 0.64837831
[21,] 1 0.5012323 0.2512338 0.12592649
[22,] 1 0.5046955 0.2547176 0.12855481
[23,] 1 0.9837646 0.9677927 0.95208017
[24,] 1 0.8422918 0.7094554 0.59756845
[25,] 1 0.4511925 0.2035747 0.09185139f <- function(x) {
theta <- head(x, p)
u <- tail(x, -p)
f1 <- outer(X = as.vector(u), Y = seq(p) - 1, FUN = "^") %*% theta - yd
f2 <- u - xd
rbind(f1, f2)
}
Df <- function(x) {
theta <- head(x, p)
u <- tail(x, -p)
D11 <- outer(X = as.vector(u), Y = seq(p) - 1, FUN = "^")
D12 <- diag(x = as.vector(theta[2] + 2 * theta[3] * u + 3 * theta[4] * u^2))
D21 <- diag(0, N, p)
D22 <- diag(1, N)
rbind(cbind(D11, D12), cbind(D21, D22))
}
func_lsm <- function(A, y) {
QR <- qr(x = A)
Q <- qr.Q(QR)
R <- qr.R(QR)
b <- t(Q) %*% y
x_hat <- solve(a = R) %*% b
return(x_hat)
}
func_levenberg_marquardt <- function(f, Df, x1, lambda1, kmax = 100, tol = 1e-6) {
n <- length(x1)
lambd <- traject_lambd <- lambda1
objectives <- residuals <- vector()
fk <- Dfk <- list()
x <- traject_x <- x1
for (k in seq(kmax)) {
fk[[k]] <- f(x)
Dfk[[k]] <- Df(x)
objectives[k] <- norm(fk[[k]], type = "2")^2
residuals[k] <- norm(
{
t(Dfk[[k]]) %*% fk[[k]]
} %>%
{
. * 2
},
type = "2"
)
if (norm(
{
t(Dfk[[k]]) %*% fk[[k]]
} * 2,
type = "2"
) < tol) {
break
}
x_hat <- func_lsm(
A = rbind(Dfk[[k]], sqrt(lambd) * diag(x = 1, nrow = n)),
y = rbind(fk[[k]], diag(x = 0, nrow = n, ncol = 1))
)
xt <- x - x_hat
if (f(xt) %>% norm(type = "2") < norm(fk[[k]], type = "2")) {
lambd <- 0.8 * lambd
x <- xt
} else {
lambd <- 2.0 * lambd
}
traject_lambd <- c(traject_lambd, lambd)
traject_x <- rbind(traject_x, x)
}
list(
x = x, objectives = objectives, residuals = residuals, traject_x = traject_x,
traject_lambd = traject_lambd, fk = fk, Dfk = Dfk
)
}# 最小二乗法による解
theta_ls <- func_lsm(A = A, y = yd)
theta_ls [,1]
[1,] 0.3275608
[2,] -4.3926668
[3,] 11.0469174
[4,] -7.0943964# 直交距離回帰(Orthogonal distance regression)による解
z <- rbind(theta_ls, xd)
result <- func_levenberg_marquardt(f = f, Df = Df, x1 = z, lambda1 = 0.01)
theta_od <- head(result$x, p)
theta_od [,1]
[1,] 0.4964045
[2,] -5.7617854
[3,] 13.9922931
[4,] -8.9298277x <- seq(min(xd), max(xd), length.out = 500)
y_ls <- outer(X = x, Y = seq(p) - 1, FUN = "^") %*% theta_ls
y_od <- outer(X = x, Y = seq(p) - 1, FUN = "^") %*% theta_od
ggplot() +
geom_point(mapping = aes(x = xd, y = yd)) +
geom_line(mapping = aes(x = x, y = y_ls, color = "最小二乗法")) +
geom_line(mapping = aes(x = x, y = y_od, color = "直交距離回帰")) +
labs(x = "x", y = TeX(input = "$\\hat{f}(x;\\theta)$")) +
theme(axis.title.y = element_text(angle = 0, vjust = 0.5), legend.title = element_blank())19 Constrained nonlinear least squares > 19.2 Penalty algorithm (p.421)
\[f(x_1,x_2)=\begin{bmatrix}x_1+\textrm{exp}(-x_2)\\x_1^2+2x_2+1\end{bmatrix},\quad g(x_1,x_2)=x_1^2+x_1^3+x_2+x_2^2\]
f <- function(x) {
c(x[1] + exp(-x[2]), x[1]^2 + 2 * x[2] + 1)
}
Df <- function(x) {
rbind(c(1, -exp(-x[2])), c(2 * x[1], 2))
}
g <- function(x) {
x[1] + x[1]^3 + x[2] + x[2]^2
}
Dg <- function(x) {
c(1 + 3 * x[1]^2, 1 + 2 * x[2])
}
func_lsm <- function(A, y) {
QR <- qr(x = A)
Q <- qr.Q(QR)
R <- qr.R(QR)
b <- t(Q) %*% y
x_hat <- solve(a = R) %*% b
return(x_hat)
}
func_levenberg_marquardt <- function(F, DF, x1, lambda1, kmax = 100, tol = 1e-6, mu) {
n <- length(x1)
lambd <- traject_lambd <- lambda1
objectives <- residuals <- vector()
fk <- Dfk <- list()
x <- traject_x <- x1
for (k in seq(kmax)) {
fk[[k]] <- F(x, mu)
Dfk[[k]] <- DF(x, mu)
objectives[k] <- norm(fk[[k]], type = "2")^2
residuals[k] <- norm(
{
t(Dfk[[k]]) %*% fk[[k]]
} %>%
{
. * 2
},
type = "2"
)
if (norm(
{
t(Dfk[[k]]) %*% fk[[k]]
} * 2,
type = "2"
) < tol) {
break
}
x_hat <- func_lsm(
A = rbind(Dfk[[k]], sqrt(lambd) * diag(x = 1, nrow = n)),
y = rbind(fk[[k]] %>% matrix(ncol = 1), diag(x = 0, nrow = n, ncol = 1))
)
xt <- x - x_hat
if (F(xt, mu) %>% norm(type = "2") < norm(fk[[k]], type = "2")) {
lambd <- 0.8 * lambd
x <- xt
} else {
lambd <- 2.0 * lambd
}
traject_lambd <- c(traject_lambd, lambd)
traject_x <- cbind(traject_x, x)
}
list(
x = x, objectives = objectives, residuals = residuals, traject_x = traject_x,
traject_lambd = traject_lambd, fk = fk, Dfk = Dfk
)
}
F <- function(x, mu) {
c(f(x = x), sqrt(mu) * g(x))
}
DF <- function(x, mu) {
rbind(Df(x), sqrt(mu) * Dg(x))
}
func_penalty_method <- function(f, Df, g, Dg, x1, lambda1, kmax, feas_tol, oc_tol) {
x <- x1
mu <- 1
feas_res <- oc_res <- lm_iters <- vector()
feas_res[1] <- norm(x = g(x), type = "2")
oc_res[1] <- norm(sweep(2 * t(Df(x)) %*% diag(f(x)), 2, 2 * mu * t(Dg(x)) * g(x), "+"), type = "f") # フロベニウスノルム
for (k in seq(kmax)) {
result <- func_levenberg_marquardt(F = F, DF = DF, x1 = x, lambda1 = lambda1, tol = oc_tol, mu = mu)
x <- result$x
feas_res[k + 1] <- norm(x = g(x), type = "2")
oc_res[k + 1] <- tail(result$residuals, 1)
lm_iters[k] <- length(result$residuals)
if (norm(x = g(x), type = "2") < feas_tol) {
break
}
mu <- 2 * mu
}
return(list(x = x, lm_iters = lm_iters, feas_res = feas_res, oc_res = oc_res))
}x1 <- c(0.5, -0.5)
lambda1 <- 1.0
kmax <- 100
feas_tol <- 1e-4
oc_tol <- 1e-4
result <- func_penalty_method(
f = f, Df = Df, g = g, Dg = Dg, x1 = x1, lambda1 = lambda1,
kmax = kmax, feas_tol = feas_tol, oc_tol = oc_tol
)
result$x [,1]
[1,] -0.00003334955
[2,] -0.00002768250cum_lm_iters <- cumsum(result$lm_iters)
itr <- cum_lm_iters %>%
sapply(function(x) rep(x, 2)) %>%
as.vector() %>%
c(0, .)
feas_res <- result$feas_res %>%
head(-1) %>%
sapply(function(x) rep(x, 2)) %>%
as.vector() %>%
c(., tail(result$feas_res, 1))
oc_res <- result$oc_res %>%
head(-1) %>%
sapply(function(x) rep(x, 2)) %>%
as.vector() %>%
c(., tail(result$oc_res, 1))
ybreaks <- seq(1, -5, -1) %>% 10^.
ylabels <- seq(1, -5, -1) %>%
paste0("$10^{", ., "}$") %>%
TeX()
ggplot(mapping = aes(x = itr)) +
geom_path(mapping = aes(y = feas_res, col = "Feasibility")) +
geom_point(mapping = aes(y = feas_res, col = "Feasibility")) +
geom_path(mapping = aes(y = oc_res, col = "Optimality condition")) +
geom_point(mapping = aes(y = oc_res, col = "Optimality condition")) +
scale_y_log10(breaks = ybreaks, labels = ylabels) +
labs(x = "Cumulative Levenberg-Marquardt iterations", y = "Residual") +
scale_x_continuous(breaks = pretty_breaks(10)) +
theme(legend.title = element_blank())19 Constrained nonlinear least squares > 19.3 Augmented Lagrangian algorithm (p.422)
Example. (p.424)
\[f(x_1,x_2)=\begin{bmatrix}x_1+\textrm{exp}(-x_2)\\x_1^2+2x_2+1\end{bmatrix},\quad g(x_1,x_2)=x_1+x_1^3+x_2+x_2^2\]
f <- function(x) {
c(x[1] + exp(-x[2]), x[1]^2 + 2 * x[2] + 1)
}
Df <- function(x) {
rbind(c(1, -exp(-x[2])), c(2 * x[1], 2))
}
g <- function(x) {
x[1] + x[1]^3 + x[2] + x[2]^2
}
Dg <- function(x) {
c(1 + 3 * x[1]^2, 1 + 2 * x[2])
}
F <- function(x, mu, z) {
c(f(x = x), sqrt(mu) * (g(x) + z / (2 * mu)))
}
DF <- function(x, mu) {
rbind(Df(x), sqrt(mu) * Dg(x))
}
func_lsm <- function(A, y) {
QR <- qr(x = A)
Q <- qr.Q(QR)
R <- qr.R(QR)
b <- t(Q) %*% y
x_hat <- solve(a = R) %*% b
return(x_hat)
}
func_levenberg_marquardt <- function(F, DF, x1, lambda1, kmax = 100, tol = 1e-6, mu, z) {
n <- length(x1)
lambd <- lambda1
objectives <- residuals <- vector()
fk <- Dfk <- list()
x <- x1
for (k in seq(kmax)) {
fk[[k]] <- F(x, mu, z)
Dfk[[k]] <- DF(x, mu)
objectives[k] <- norm(fk[[k]], type = "2")^2
residuals[k] <- norm(
{
t(Dfk[[k]]) %*% fk[[k]]
} %>%
{
. * 2
},
type = "2"
)
if (norm(
{
t(Dfk[[k]]) %*% fk[[k]]
} * 2,
type = "2"
) < tol) {
break
}
x_hat <- func_lsm(
A = rbind(Dfk[[k]], sqrt(lambd) * diag(x = 1, nrow = n)),
y = rbind(fk[[k]] %>% matrix(ncol = 1), diag(x = 0, nrow = n, ncol = 1))
)
xt <- x - x_hat
if (F(xt, mu, z) %>% norm(type = "2") < norm(fk[[k]], type = "2")) {
lambd <- 0.8 * lambd
x <- xt
} else {
lambd <- 2.0 * lambd
}
}
list(x = x, objectives = objectives, residuals = residuals, fk = fk, Dfk = Dfk)
}
func_aug_lag_method <- function(f, Df, g, Dg, x1, lambda1, kmax, feas_tol, oc_tol) {
feas_res <- oc_res <- lm_iters <- z <- vector()
x <- list()
x[[1]] <- x1
z[1] <- rep(0, length(g(x[[1]])))
mu <- 1
feas_res[1] <- norm(x = g(x[[1]]), type = "2")
oc_res[1] <- norm(sweep(2 * t(Df(x[[1]])) %*% diag(f(x[[1]])), 2, 2 * mu * t(Dg(x[[1]])) * g(x[[1]]), "+"),
type = "f"
) # フロベニウスノルム
for (k in seq(kmax)) {
result <- func_levenberg_marquardt(F = F, DF = DF, x1 = x[[k]], lambda1 = lambda1, tol = oc_tol, mu = mu, z = z[k])
x[[k + 1]] <- result$x
z[k + 1] <- z[k] + 2 * mu * g(x[[k + 1]])
feas_res[k + 1] <- norm(x = g(x[[k + 1]]), type = "2")
oc_res[k + 1] <- tail(result$residuals, 1)
lm_iters[k] <- length(result$residuals)
if (norm(x = g(x[[k + 1]]), type = "2") < feas_tol) {
break
}
if (norm(x = g(x[[k + 1]]), type = "2") >= 0.25 * feas_res[length(feas_res) - 1]) {
mu <- 2 * mu
}
}
return(list(x = x, lm_iters = lm_iters, feas_res = feas_res, oc_res = oc_res, z = z))
}x1 <- c(0.5, -0.5)
lambda1 <- 1
feas_tol <- 1e-4
oc_tol <- 1e-4
result <- func_aug_lag_method(
f = f, Df = Df, g = g, Dg = Dg, x1 = x1,
lambda1 = lambda1, kmax = kmax, feas_tol = feas_tol, oc_tol = oc_tol
)result$z[1] 0.0000000 -0.8931618 -1.5692103 -1.8981747 -1.9760847 -1.9943664 -1.9987162
[8] -1.9996889 -1.9999581result$x %>% Reduce(function(x, y) cbind(x, y), .) x
[1,] 0.5 -0.2740307 -0.09908671 -0.02317636 -0.005426782 -0.001266552
[2,] -0.5 -0.1869066 -0.07450331 -0.01826536 -0.004330570 -0.001019695
[1,] -0.0003037159 -0.00006453201 -0.00001864661
[2,] -0.0002400616 -0.00005706300 -0.00001500857cum_lm_iters <- cumsum(result$lm_iters)
itr <- cum_lm_iters %>%
sapply(function(x) rep(x, 2)) %>%
as.vector() %>%
c(0, .)
feas_res <- result$feas_res %>%
head(-1) %>%
sapply(function(x) rep(x, 2)) %>%
as.vector() %>%
c(., tail(result$feas_res, 1))
oc_res <- result$oc_res %>%
head(-1) %>%
sapply(function(x) rep(x, 2)) %>%
as.vector() %>%
c(., tail(result$oc_res, 1))
ybreaks <- seq(1, -5, -1) %>% 10^.
ylabels <- seq(1, -5, -1) %>%
paste0("$10^{", ., "}$") %>%
TeX()
ggplot(mapping = aes(x = itr)) +
geom_path(mapping = aes(y = feas_res, col = "Feasibility")) +
geom_point(mapping = aes(y = feas_res, col = "Feasibility")) +
geom_path(mapping = aes(y = oc_res, col = "Optimality condition")) +
geom_point(mapping = aes(y = oc_res, col = "Optimality condition")) +
scale_y_log10(breaks = ybreaks, labels = ylabels) +
labs(x = "Cumulative Levenberg-Marquardt iterations", y = "Residual") +
scale_x_continuous(breaks = pretty_breaks(10)) +
theme(legend.title = element_blank())参考引用資料
- Stephen Boyd,Lieven Vandenberghe(2018),『Introduction to Applied Linear Algebra Vectors, Matrices, and Least Squares』,Cambridge University Press
- http://vmls-book.stanford.edu/
- https://ses.library.usyd.edu.au/handle/2123/21370
- https://github.com/jessica-wyleung/VMLS-py
- http://www.seas.ucla.edu/~vandenbe/133A/lectures/qr.pdf
- R code in this file is written with reference to the python code in the https://ses.library.usyd.edu.au/handle/2123/21370 and the julia code in the http://vmls-book.stanford.edu/vmls-julia-companion.pdf.
最終更新
Sys.time()[1] "2024-06-07 08:59:32 JST"R、Quarto、Package
R.Version()$version.string[1] "R version 4.3.3 (2024-02-29 ucrt)"quarto::quarto_version()[1] '1.4.553'packageVersion(pkg = 'tidyverse')[1] '2.0.0'