Rで回帰分析:ロバスト回帰

Rでデータサイエンス

ロバスト回帰

library(ggplot2)
library(dplyr)
seed <- 20230327

サンプルデータの作成

# サンプルデータの作成
set.seed(seed = seed)
n <- 10
x <- runif(n = n, min = 0, max = 10) %>%
    sort()
b0 <- 5
b1 <- 10
y <- x * b1 + b0 + rnorm(n = n)
y[n] <- y[n] * 5
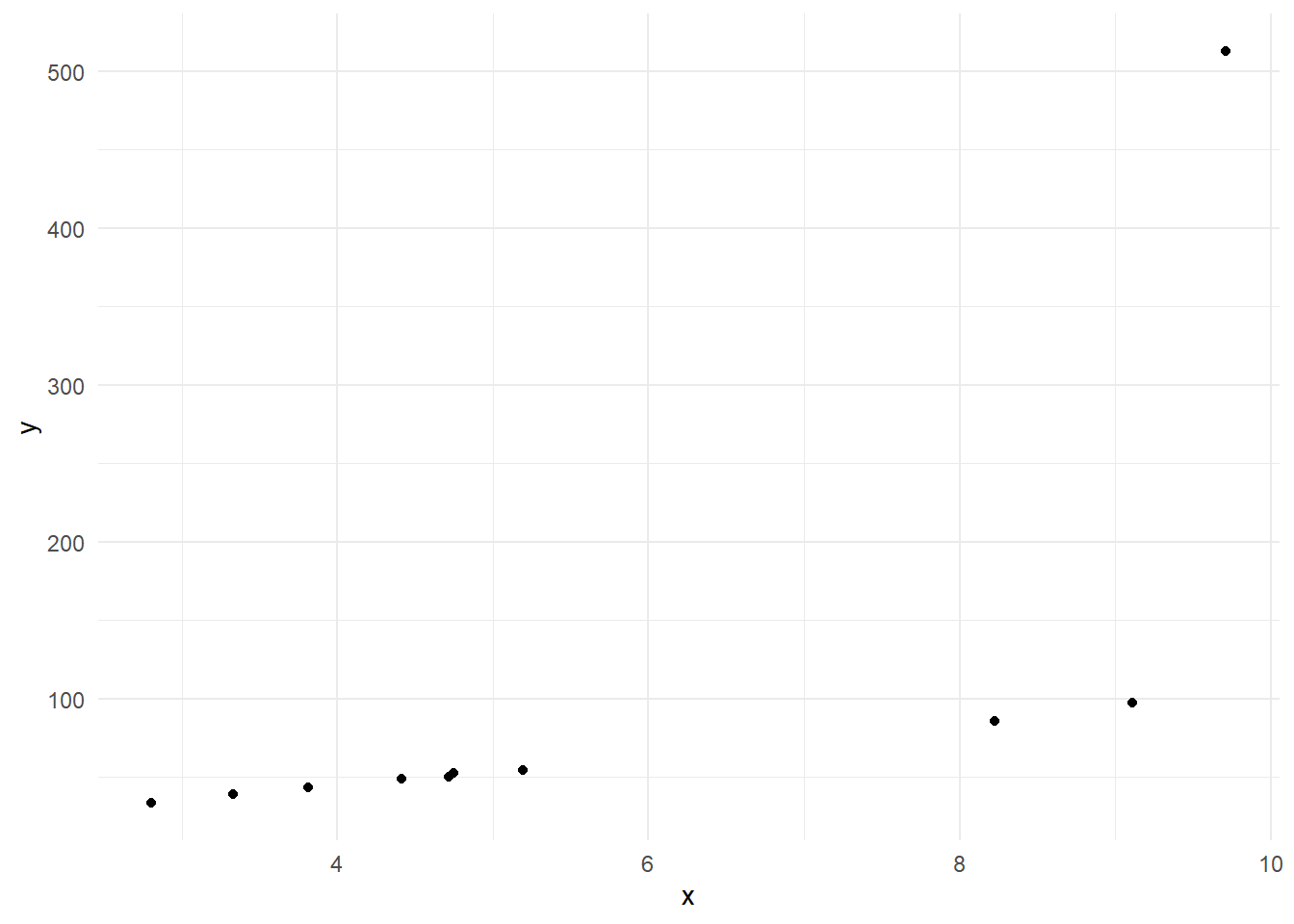
(g <- ggplot(data = data.frame(x, y), mapping = aes(x = x, y = y)) + geom_point() + theme_minimal())

Figure 1

# 線形回帰
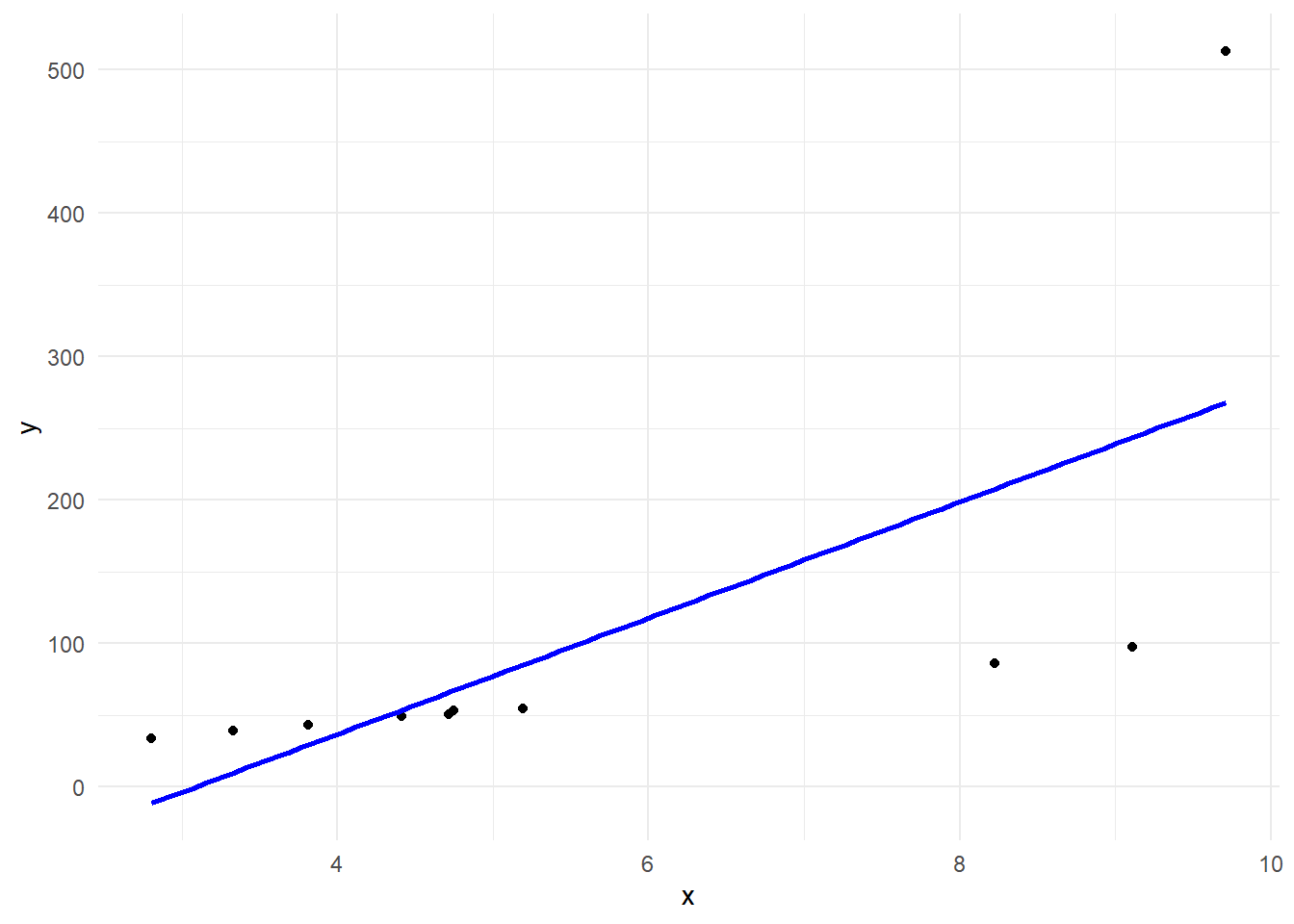
(g <- g + geom_smooth(method = "lm", se = F, col = "blue"))
lm(y ~ x) %>%
    summary()

Call:
lm(formula = y ~ x)

Residuals:
     Min       1Q   Median       3Q      Max 
-146.421  -26.938   -9.357   25.520  244.812 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept)  -124.82      91.64  -1.362   0.2103  
x              40.43      15.07   2.682   0.0278 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 112.2 on 8 degrees of freedom
Multiple R-squared:  0.4735,    Adjusted R-squared:  0.4077 
F-statistic: 7.195 on 1 and 8 DF,  p-value: 0.02782

Figure 2

rlm {MASS} によるロバスト線形回帰

# ロバスト線形回帰
library(MASS)
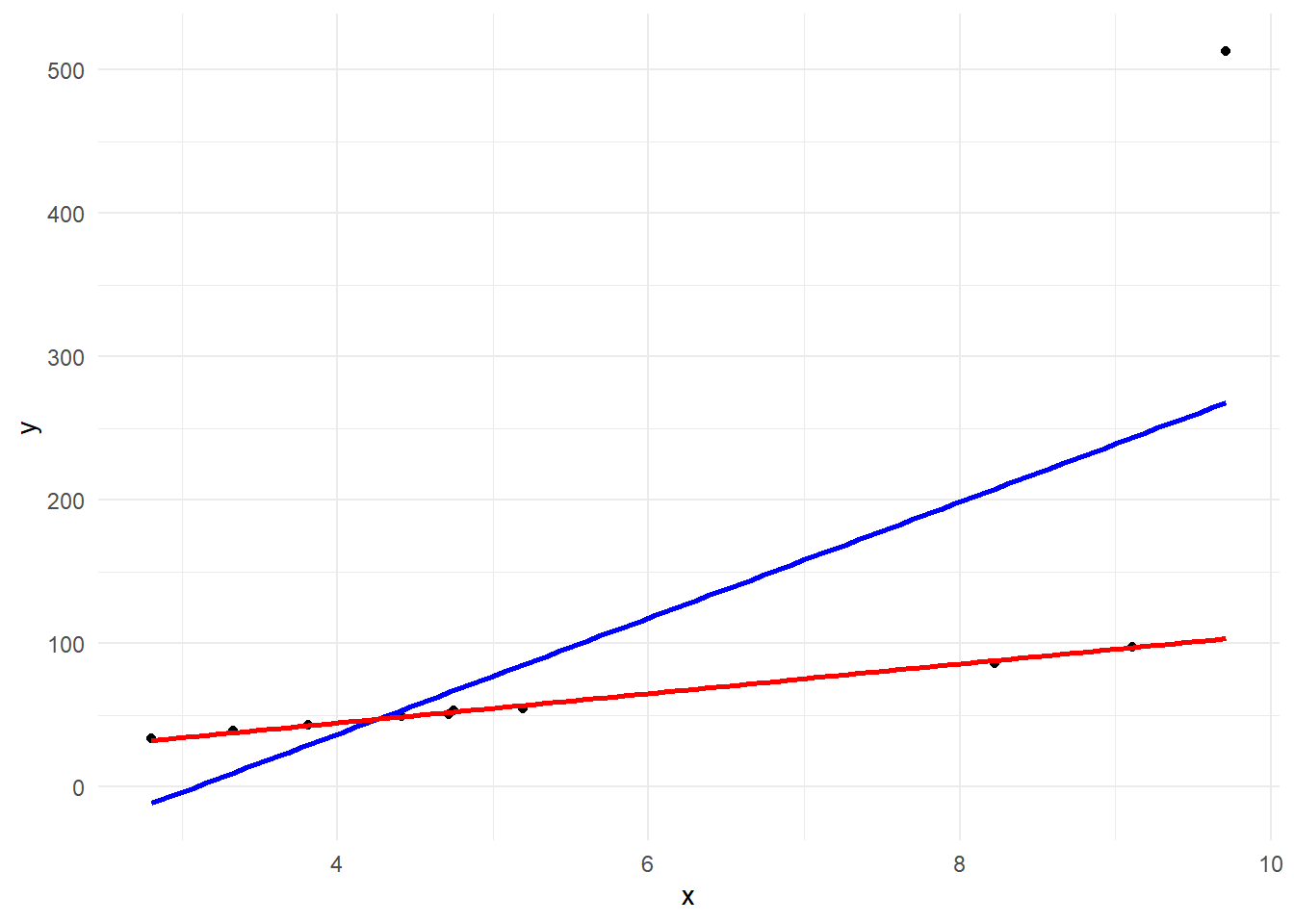
packageVersion("MASS")

[1] '7.3.60.0.1'

g + geom_smooth(method = "rlm", se = F, col = "red")
result <- rlm(y ~ x)
result %>%
    summary()

Call: rlm(formula = y ~ x)
Residuals:
     Min       1Q   Median       3Q      Max 
 -2.5882  -1.2076   0.2692   0.9066 409.3434 

Coefficients:
            Value   Std. Error t value
(Intercept)  3.6571  1.7619     2.0757
x           10.2574  0.2898    35.3996

Residual standard error: 1.779 on 8 degrees of freedom

Figure 3

rlm {MASS}

• 繰返し加重最小二乗(IRLS: Iteratively Reweighted Least Squares)によるロバスト回帰。
• M推定とMM推定から選択。
• \(\psi\,\)関数(影響関数)のデフォルトはHuber。Hampelおよびbisquare(Tukey)も可能。但しMM推定の場合はbisquare(Tukey)。
• 尺度パラメータ(\(s\))はMAD(中央絶対偏差)、Huberおよびproposal 2(Huber’s proposal 2)から選択。

methods("rlm")

[1] rlm.default* rlm.formula*
see '?methods' for accessing help and source code

rlm.formula

getS3method(f = "rlm", class = "formula")

function (formula, data, weights, ..., subset, na.action, method = c("M", 
    "MM", "model.frame"), wt.method = c("inv.var", "case"), model = TRUE, 
    x.ret = TRUE, y.ret = FALSE, contrasts = NULL) 
{
    mf <- match.call(expand.dots = FALSE)
    mf$method <- mf$wt.method <- mf$model <- mf$x.ret <- mf$y.ret <- mf$contrasts <- mf$... <- NULL
    mf[[1L]] <- quote(stats::model.frame)
    mf <- eval.parent(mf)
    method <- match.arg(method)
    wt.method <- match.arg(wt.method)
    if (method == "model.frame") 
        return(mf)
    mt <- attr(mf, "terms")
    y <- model.response(mf)
    offset <- model.offset(mf)
    if (!is.null(offset)) 
        y <- y - offset
    x <- model.matrix(mt, mf, contrasts)
    xvars <- as.character(attr(mt, "variables"))[-1L]
    if ((yvar <- attr(mt, "response")) > 0L) 
        xvars <- xvars[-yvar]
    xlev <- if (length(xvars) > 0L) {
        xlev <- lapply(mf[xvars], levels)
        xlev[!sapply(xlev, is.null)]
    }
    weights <- model.weights(mf)
    if (!length(weights)) 
        weights <- rep(1, nrow(x))
    fit <- rlm.default(x, y, weights, method = method, wt.method = wt.method, 
        ...)
    fit$terms <- mt
    cl <- match.call()
    cl[[1L]] <- as.name("rlm")
    fit$call <- cl
    fit$contrasts <- attr(x, "contrasts")
    fit$xlevels <- .getXlevels(mt, mf)
    fit$na.action <- attr(mf, "na.action")
    if (model) 
        fit$model <- mf
    if (!x.ret) 
        fit$x <- NULL
    if (y.ret) 
        fit$y <- y
    fit$offset <- offset
    if (!is.null(offset)) 
        fit$fitted.values <- fit$fitted.values + offset
    fit
}
<bytecode: 0x0000022eee84d5e0>
<environment: namespace:MASS>

rlm.default

getS3method(f = "rlm", class = "default")

function (x, y, weights, ..., w = rep(1, nrow(x)), init = "ls", 
    psi = psi.huber, scale.est = c("MAD", "Huber", "proposal 2"), 
    k2 = 1.345, method = c("M", "MM"), wt.method = c("inv.var", 
        "case"), maxit = 20, acc = 0.0001, test.vec = "resid", 
    lqs.control = NULL) 
{
    irls.delta <- function(old, new) sqrt(sum((old - new)^2)/max(0.00000000000000000001, 
        sum(old^2)))
    irls.rrxwr <- function(x, w, r) {
        w <- sqrt(w)
        max(abs((matrix(r * w, 1L, length(r)) %*% x)/sqrt(matrix(w, 
            1L, length(r)) %*% (x^2))))/sqrt(sum(w * r^2))
    }
    wmad <- function(x, w) {
        o <- sort.list(abs(x))
        x <- abs(x)[o]
        w <- w[o]
        p <- cumsum(w)/sum(w)
        n <- sum(p < 0.5)
        if (p[n + 1L] > 0.5) 
            x[n + 1L]/0.6745
        else (x[n + 1L] + x[n + 2L])/(2 * 0.6745)
    }
    method <- match.arg(method)
    wt.method <- match.arg(wt.method)
    nmx <- deparse(substitute(x))
    if (is.null(dim(x))) {
        x <- as.matrix(x)
        colnames(x) <- nmx
    }
    else x <- as.matrix(x)
    if (is.null(colnames(x))) 
        colnames(x) <- paste("X", seq(ncol(x)), sep = "")
    if (qr(x)$rank < ncol(x)) 
        stop("'x' is singular: singular fits are not implemented in 'rlm'")
    if (!(any(test.vec == c("resid", "coef", "w", "NULL")) || 
        is.null(test.vec))) 
        stop("invalid 'test.vec'")
    xx <- x
    yy <- y
    if (!missing(weights)) {
        if (length(weights) != nrow(x)) 
            stop("length of 'weights' must equal number of observations")
        if (any(weights < 0)) 
            stop("negative 'weights' value")
        if (wt.method == "inv.var") {
            fac <- sqrt(weights)
            y <- y * fac
            x <- x * fac
            wt <- NULL
        }
        else {
            w <- w * weights
            wt <- weights
        }
    }
    else wt <- NULL
    if (method == "M") {
        scale.est <- match.arg(scale.est)
        if (!is.function(psi)) 
            psi <- get(psi, mode = "function")
        arguments <- list(...)
        if (length(arguments)) {
            pm <- pmatch(names(arguments), names(formals(psi)), 
                nomatch = 0L)
            if (any(pm == 0L)) 
                warning("some of ... do not match")
            pm <- names(arguments)[pm > 0L]
            formals(psi)[pm] <- unlist(arguments[pm])
        }
        if (is.character(init)) {
            temp <- if (init == "ls") 
                lm.wfit(x, y, w, method = "qr")
            else if (init == "lts") {
                if (is.null(lqs.control)) 
                  lqs.control <- list(nsamp = 200L)
                do.call("lqs", c(list(x, y, intercept = FALSE), 
                  lqs.control))
            }
            else stop("'init' method is unknown")
            coef <- temp$coefficients
            resid <- temp$residuals
        }
        else {
            if (is.list(init)) 
                coef <- init$coef
            else coef <- init
            resid <- drop(y - x %*% coef)
        }
    }
    else if (method == "MM") {
        scale.est <- "MM"
        temp <- do.call("lqs", c(list(x, y, intercept = FALSE, 
            method = "S", k0 = 1.548), lqs.control))
        coef <- temp$coefficients
        resid <- temp$residuals
        psi <- psi.bisquare
        if (length(arguments <- list(...))) 
            if (match("c", names(arguments), nomatch = 0L)) {
                c0 <- arguments$c
                if (c0 > 1.548) 
                  formals(psi)$c <- c0
                else warning("'c' must be at least 1.548 and has been ignored")
            }
        scale <- temp$scale
    }
    else stop("'method' is unknown")
    done <- FALSE
    conv <- NULL
    n1 <- (if (is.null(wt)) 
        nrow(x)
    else sum(wt)) - ncol(x)
    theta <- 2 * pnorm(k2) - 1
    gamma <- theta + k2^2 * (1 - theta) - 2 * k2 * dnorm(k2)
    if (scale.est != "MM") 
        scale <- if (is.null(wt)) 
            mad(resid, 0)
        else wmad(resid, wt)
    for (iiter in 1L:maxit) {
        if (!is.null(test.vec)) 
            testpv <- get(test.vec)
        if (scale.est != "MM") {
            scale <- if (scale.est == "MAD") 
                if (is.null(wt)) 
                  median(abs(resid))/0.6745
                else wmad(resid, wt)
            else if (is.null(wt)) 
                sqrt(sum(pmin(resid^2, (k2 * scale)^2))/(n1 * 
                  gamma))
            else sqrt(sum(wt * pmin(resid^2, (k2 * scale)^2))/(n1 * 
                gamma))
            if (scale == 0) {
                done <- TRUE
                break
            }
        }
        w <- psi(resid/scale)
        if (!is.null(wt)) 
            w <- w * weights
        temp <- lm.wfit(x, y, w, method = "qr")
        coef <- temp$coefficients
        resid <- temp$residuals
        if (!is.null(test.vec)) 
            convi <- irls.delta(testpv, get(test.vec))
        else convi <- irls.rrxwr(x, w, resid)
        conv <- c(conv, convi)
        done <- (convi <= acc)
        if (done) 
            break
    }
    if (!done) 
        warning(gettextf("'rlm' failed to converge in %d steps", 
            maxit), domain = NA)
    fitted <- drop(xx %*% coef)
    cl <- match.call()
    cl[[1L]] <- as.name("rlm")
    fit <- list(coefficients = coef, residuals = yy - fitted, 
        wresid = resid, effects = temp$effects, rank = temp$rank, 
        fitted.values = fitted, assign = temp$assign, qr = temp$qr, 
        df.residual = NA, w = w, s = scale, psi = psi, k2 = k2, 
        weights = if (!missing(weights)) weights, conv = conv, 
        converged = done, x = xx, call = cl)
    class(fit) <- c("rlm", "lm")
    fit
}
<bytecode: 0x0000022eee89c7f0>
<environment: namespace:MASS>

\(\psi\)関数

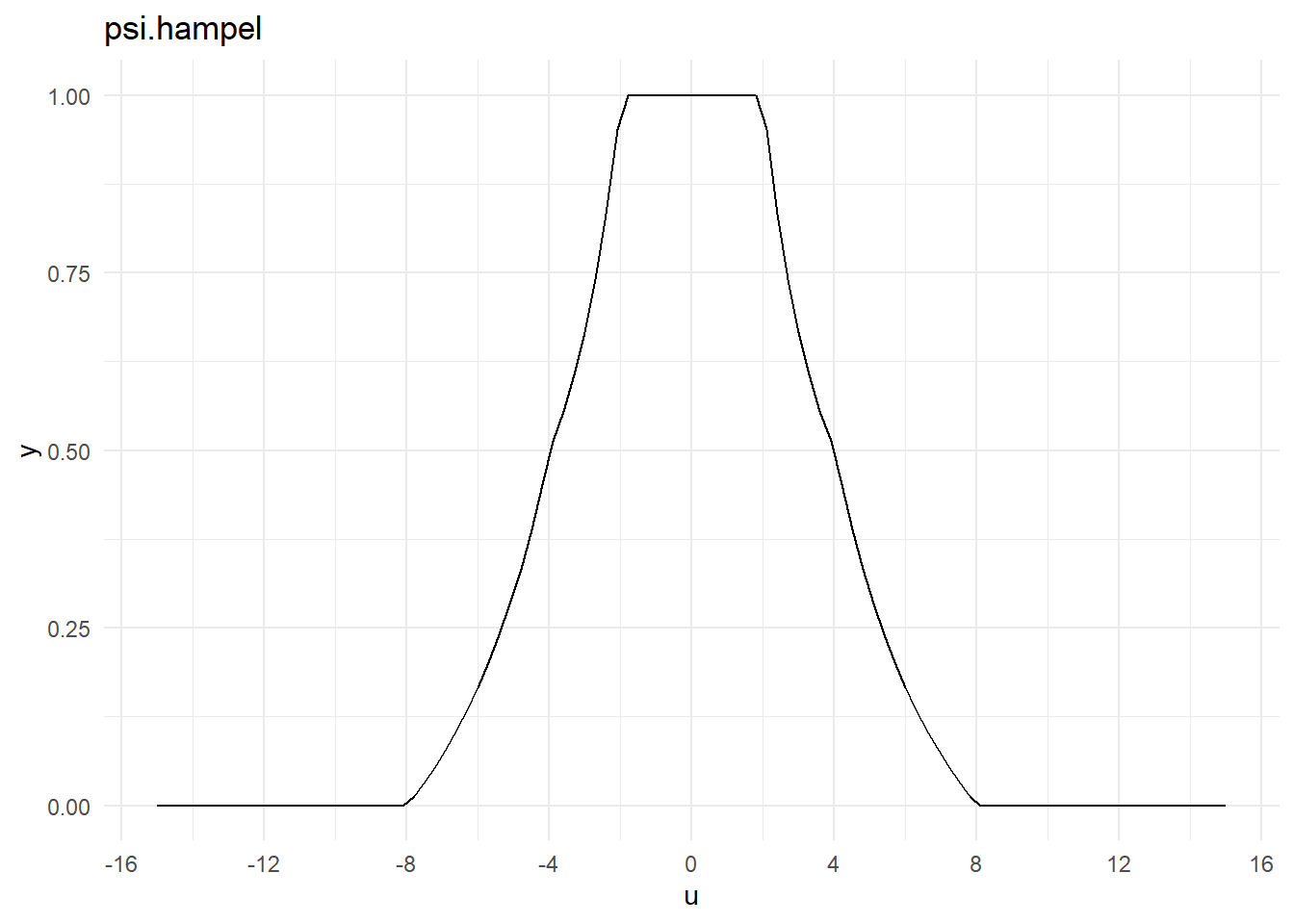
psi.hampel

psi.hampel

function (u, a = 2, b = 4, c = 8, deriv = 0) 
{
    U <- pmin(abs(u) + 0.00000000000000000000000000000000000000000000000001, 
        c)
    if (!deriv) 
        return(ifelse(U <= a, U, ifelse(U <= b, a, a * (c - U)/(c - 
            b)))/U)
    ifelse(abs(u) <= c, ifelse(U <= a, 1, ifelse(U <= b, 0, -a/(c - 
        b))), 0)
}
<bytecode: 0x0000022ecc9522c0>
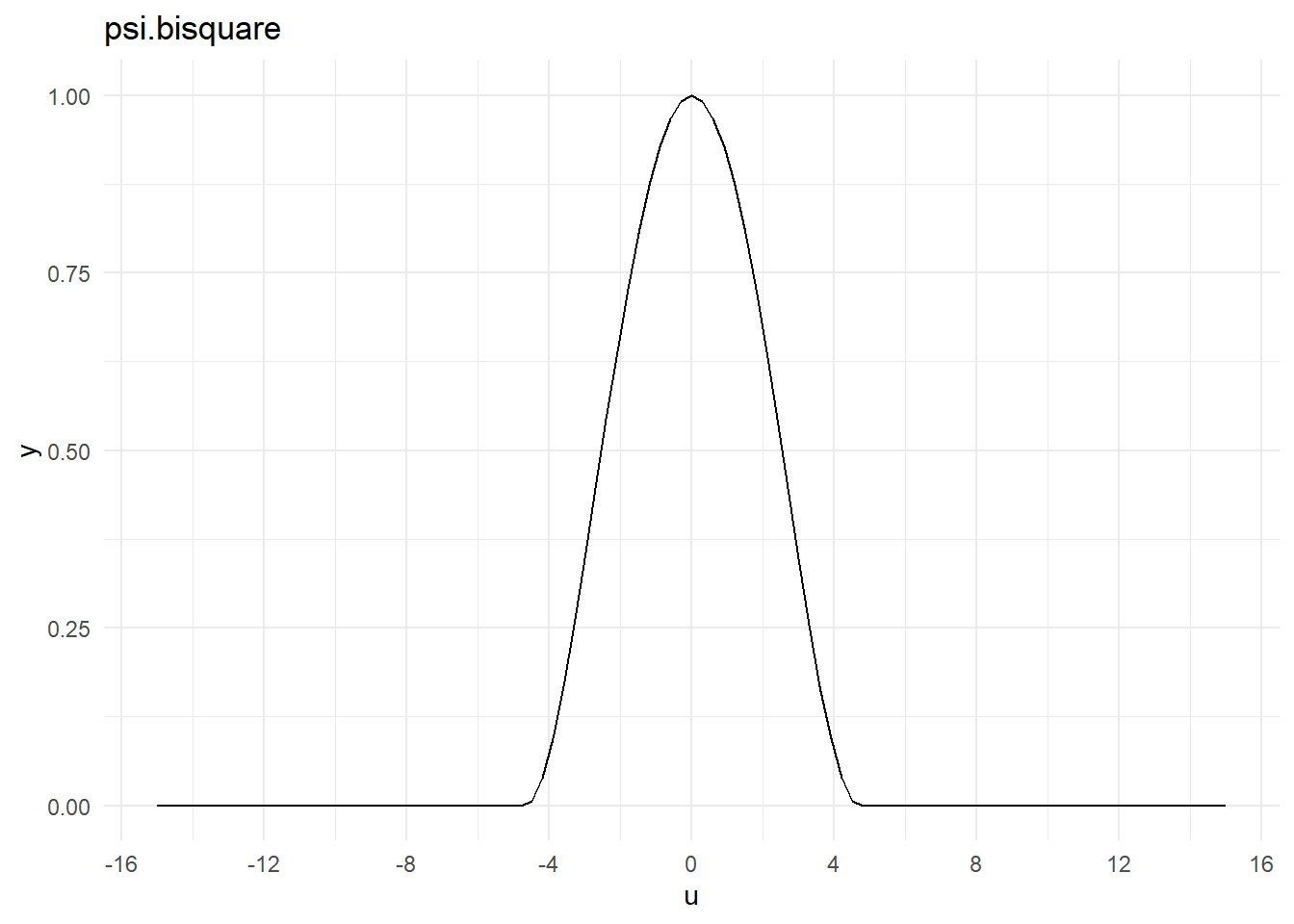
<environment: namespace:MASS>

u <- c(seq(-15, 0, by = 0.01), seq(0, 15, by = 0.01)) %>%
    unique()
ggplot(data = data.frame(x = u), mapping = aes(x = u)) + stat_function(fun = function(x) psi.hampel(u = x, deriv = 0)) + scale_x_continuous(n.breaks = 10) + theme_minimal() + labs(title = "psi.hampel")

Figure 4

psi.bisquare

psi.bisquare

function (u, c = 4.685, deriv = 0) 
{
    if (!deriv) 
        return((1 - pmin(1, abs(u/c))^2)^2)
    t <- (u/c)^2
    ifelse(t < 1, (1 - t) * (1 - 5 * t), 0)
}
<bytecode: 0x0000022eedf8b0b0>
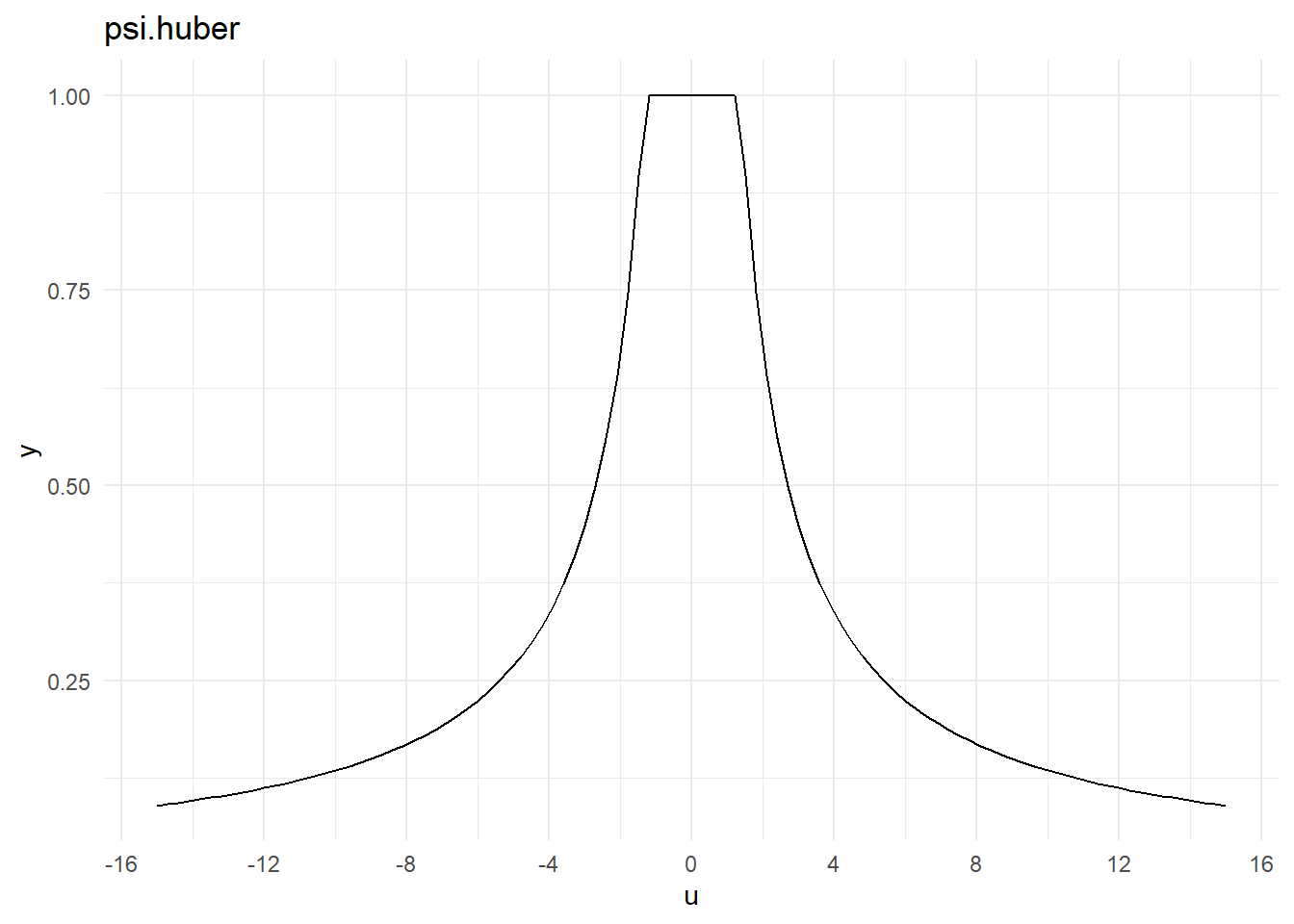
<environment: namespace:MASS>

ggplot(data = data.frame(x = u), mapping = aes(x = u)) + stat_function(fun = function(x) psi.bisquare(u = x, deriv = 0)) + scale_x_continuous(n.breaks = 10) + theme_minimal() + labs(title = "psi.bisquare")

Figure 5

psi.huber

psi.huber

function (u, k = 1.345, deriv = 0) 
{
    if (!deriv) 
        return(pmin(1, k/abs(u)))
    abs(u) <= k
}
<bytecode: 0x0000022eee8c7050>
<environment: namespace:MASS>

ggplot(data = data.frame(x = u), mapping = aes(x = u)) + stat_function(fun = function(x) psi.huber(u = x, deriv = 0)) + scale_x_continuous(n.breaks = 10) + theme_minimal() + labs(title = "psi.huber")

Figure 6

参考引用資料

1. https://rdrr.io/cran/MASS/man/rlm.html
2. https://www.stat.go.jp/training/2kenkyu/ihou/76/pdf/2-2-767.pdf
3. https://jp.mathworks.com/help/stats/robustfit.html
4. https://qiita.com/ssugasawa/items/d1a015bff9ee2c8552de
5. https://www.stats.ox.ac.uk/~ripley/StatMethods/Robust.pdf
6. https://www.stat.go.jp/training/2kenkyu/ihou/69/pdf/2-2-692.pdf

最終更新

Sys.time()

[1] "2024-04-03 04:38:02 JST"

R、Quarto、Package

R.Version()$version.string

[1] "R version 4.3.3 (2024-02-29 ucrt)"

quarto::quarto_version()

[1] '1.4.542'

packageVersion(pkg = "tidyverse")

[1] '2.0.0'

著者

• アセット･マネジメント･コンサルティング株式会社 https://www.am-consulting.co.jp
• 法人概要 https://www.contact.am-consulting.co.jp/company-brochure/
• 代表取締役 三竹道雄 https://www.contact.am-consulting.co.jp/mitake-michio/
• 公開コンテンツリスト https://www.am-consulting.co.jp/amc-all-contents.html
• Charts https://www.am-consulting.co.jp/charts.html
• 法令検索 https://www.laws.am-consulting.co.jp/
• SaECaNet https://www.saecanet.com/
• twitter https://twitter.com/amc_corporation
• youtube https://www.youtube.com/user/michiomitake
• twilog https://twilog.togetter.com/amc_corporation
• github https://github.com/am-consulting

Figure 1: Figure 2: Figure 3: Figure 4: Figure 5: Figure 6: