library(dplyr)
library(ggplot2)
library(gridExtra)
library(scales)
# ロジスティック回帰(一般化線形モデル)
# 確率分布:二項分布
# リンク関数:応答変数にロジット関数を適用
# 線形予測子:beta + alpha * x
# 二項分布:二値確率変数
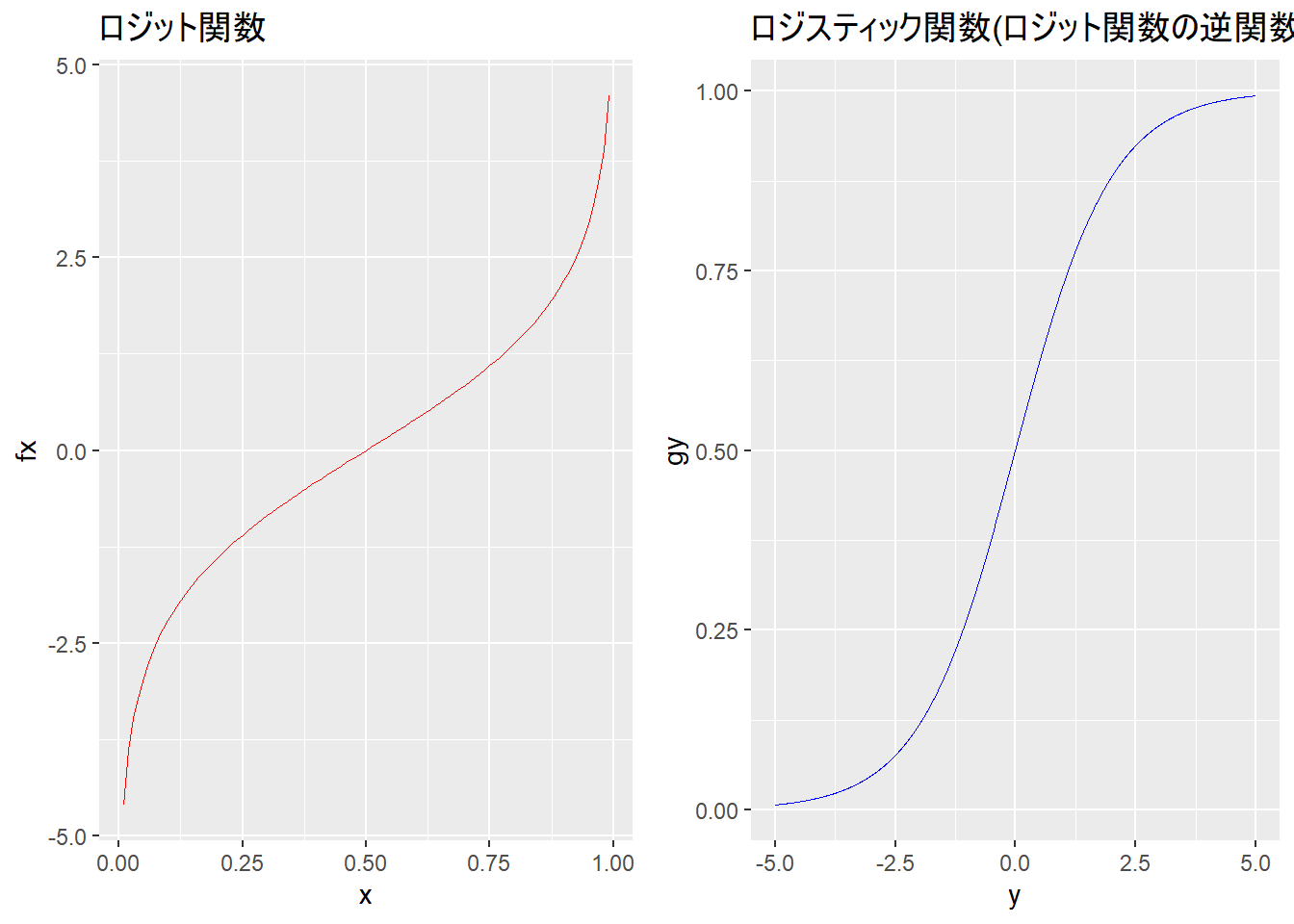
# f(x):ロジット関数
# g(x):ロジスティック関数(ロジット関数の逆関数)Rで確率・統計:一般化線形モデル:ロジスティック回帰
Rでデータサイエンス
一般化線形モデル:ロジスティック回帰
\[ \begin{aligned} &f(x) = \textrm {log}_e \left( \dfrac{x}{1-x} \right),\quad g(y) = \dfrac{1}{1+e^{-y}}\\ &\textrm{log} \left( \dfrac{p}{1-p} \right) = \beta + \alpha x,\quad p = \dfrac{1}{1 + e^{-(\beta + \alpha x)}}\\ &M \sim \textrm {Binomial} \left( m\,|\,N, \dfrac{1}{1+e^{-(\beta + \alpha x)}}\right),\quad \textrm {Binomial}(m\,|\,N,p) = {}_N \textrm{C}_m \cdot p^m \cdot (1-p)^{N-m} \end{aligned} \]
# ロジット関数とロジスティック関数の形状を確認。
gg <- list()
# ロジット関数
x <- seq(0.01, 0.99, 0.01)
fx <- log(x/(1 - x), base = exp(1))
gg[[1]] <- ggplot(mapping = aes(x = x, y = fx)) + geom_line(col = "red", size = 0.1) + labs(title = "ロジット関数")
# ロジスティック関数(ロジット関数の逆関数)
y <- seq(-5, 5, 0.01)
gy <- 1/(1 + exp(-y))
gg[[2]] <- ggplot(mapping = aes(x = y, y = gy)) + geom_line(col = "blue", size = 0.1) + labs(title = "ロジスティック関数(ロジット関数の逆関数)")
ggpubr::as_ggplot(arrangeGrob(grobs = gg, ncol = 2))# サンプルを作成。
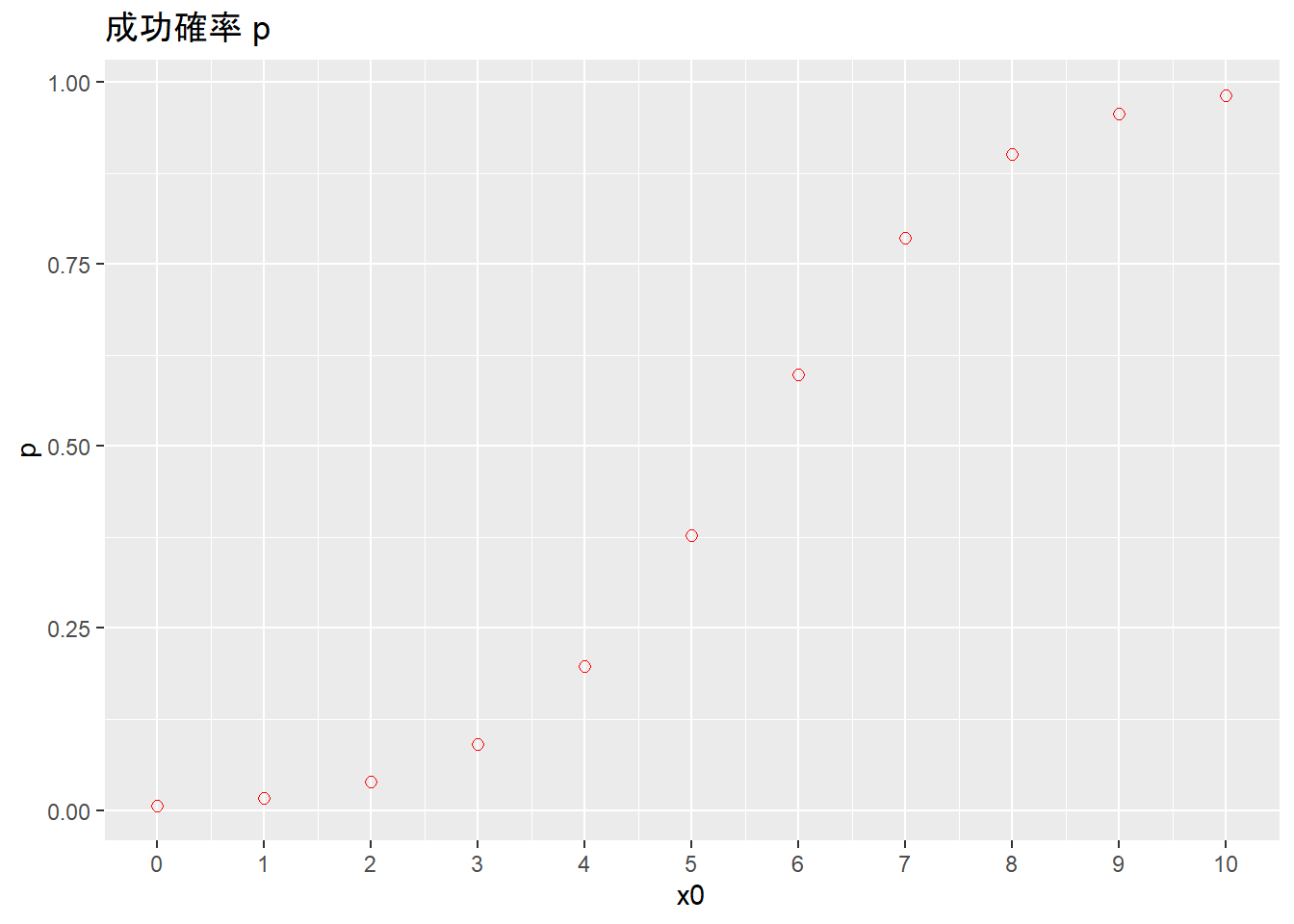
# 成功確率 p の作成。設定した数値に意味はなし。
x0 <- seq(from = 0, to = 10, by = 1)
a <- 0.9
b <- -5
p <- 1/(1 + exp(-(b + a * x0)))
g <- ggplot(mapping = aes(x = x0)) + geom_point(mapping = aes(y = p), size = 2, pch = 1, col = "red") + labs(title = "成功確率 p") + scale_x_continuous(breaks = pretty_breaks(length(x0)))
g# 二値確率変数 M の作成。
M <- as.vector(sapply(seq(10), function(i) rbinom(n = length(x0), size = 1, prob = p)))
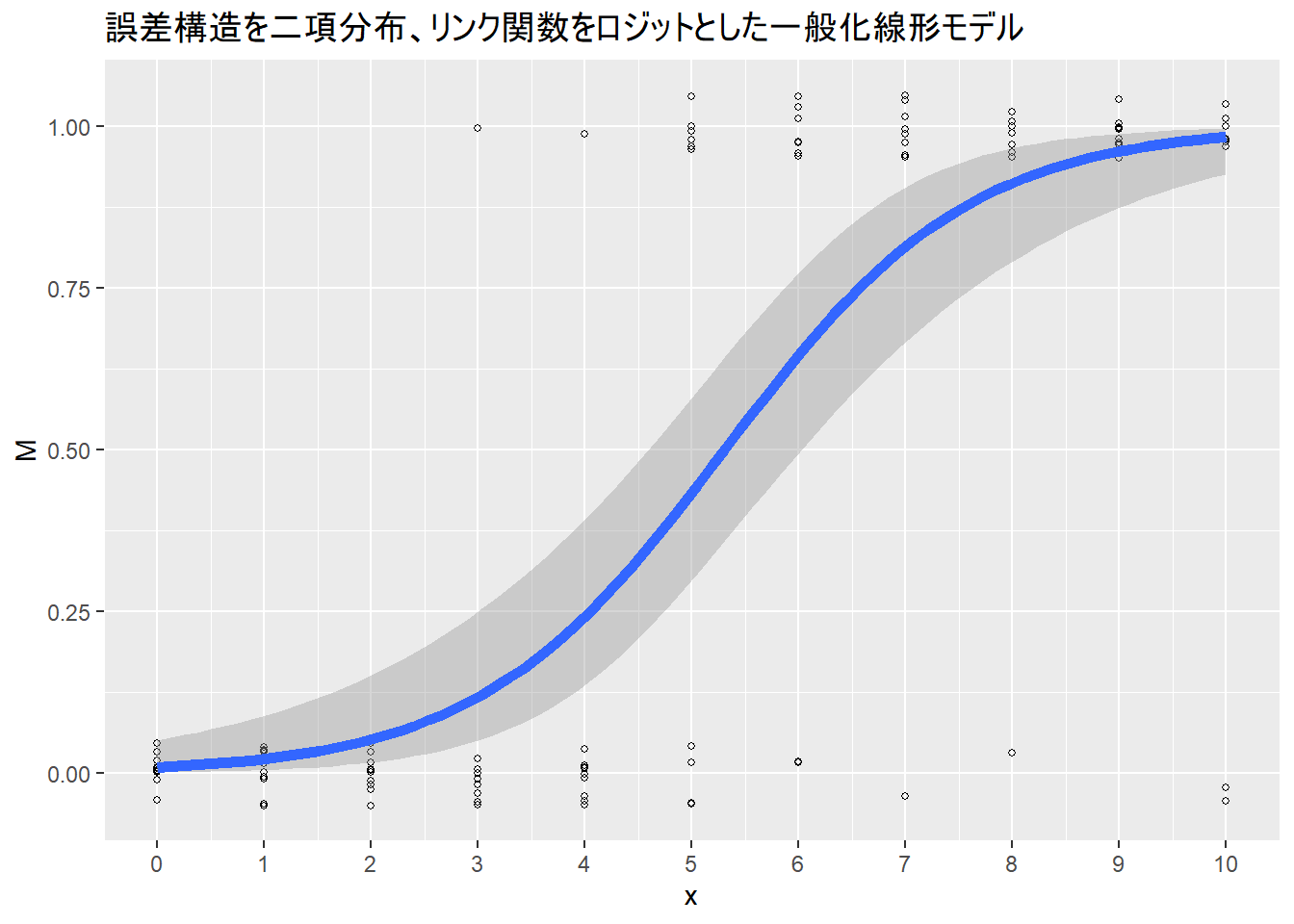
# M length(M)# 誤差構造を二項分布、リンク関数をロジットとした一般化線形モデルを解く。
x <- rep(x0, 10)
glmg <- ggplot(mapping = aes(x = x, y = M)) + geom_point(pch = 1, size = 1, position = position_jitter(w = 0, h = 0.05)) + geom_smooth(size = 2, method = "glm", method.args = list(family = binomial(link = "logit")), se = T) + scale_x_continuous(breaks = pretty_breaks(n = length(unique(x)))) + labs(title = "誤差構造を二項分布、リンク関数をロジットとした一般化線形モデル")
glmg# 推定されたパラメータを確認。
model <- glm(M ~ x, family = binomial(link = "logit"))
summary(model)
# 係数は有意。
signifdigits <- 7
a <- model$coefficients[2] %>%
as.numeric() %>%
signif(signifdigits)
b <- model$coefficients[1] %>%
as.numeric() %>%
signif(signifdigits)
list(a = a, b = b)
Call:
glm(formula = M ~ x, family = binomial(link = "logit"))
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -4.6248 0.8763 -5.278 0.0000001309 ***
x 0.8718 0.1561 5.586 0.0000000232 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 152.165 on 109 degrees of freedom
Residual deviance: 72.897 on 108 degrees of freedom
AIC: 76.897
Number of Fisher Scoring iterations: 6
$a
[1] 0.8717972
$b
[1] -4.624803# 以降、推定されたロジスティック回帰係数(a、b)による成功確率他。
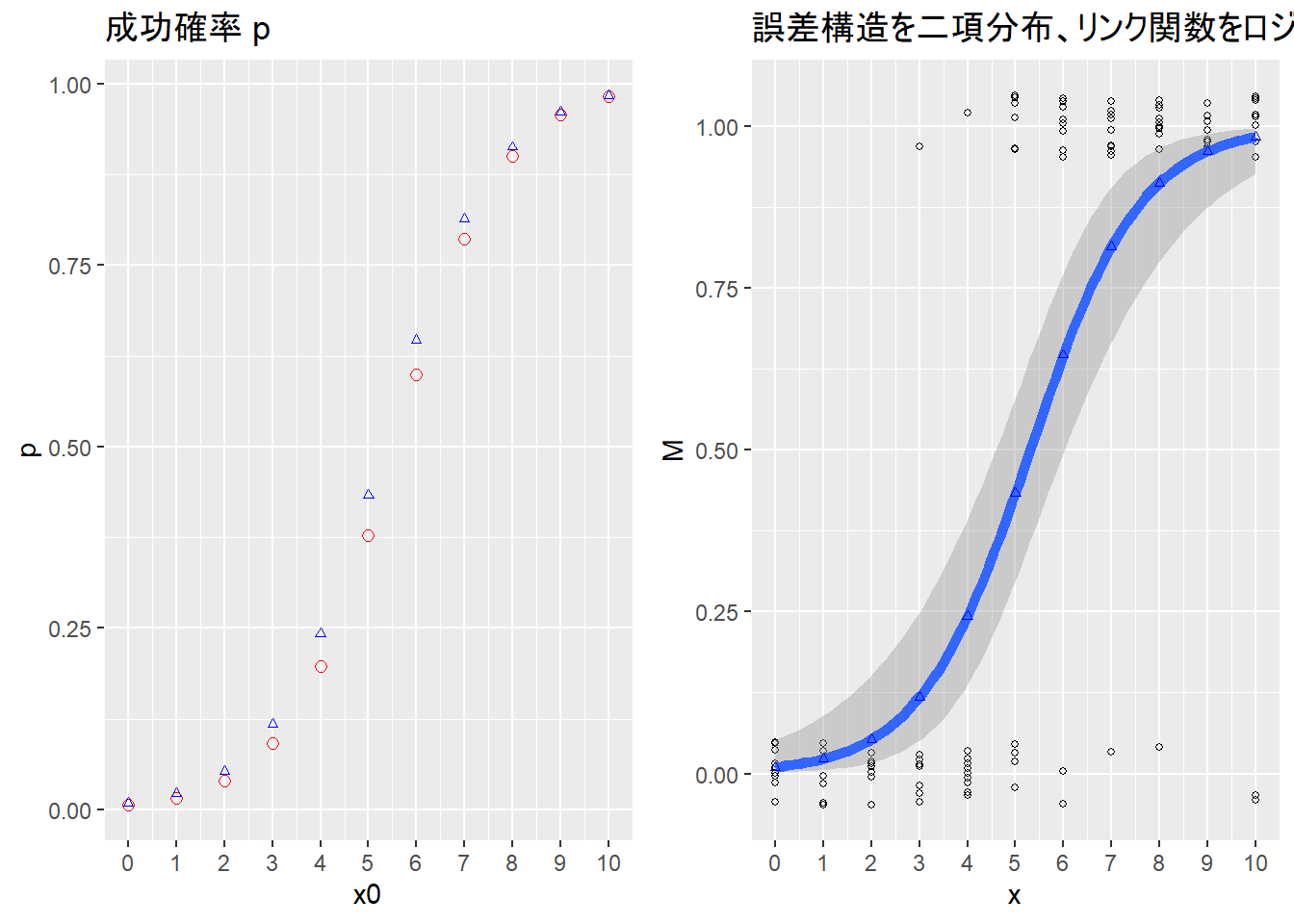
pgg <- list()
# 成功確率
1/(1 + exp(-(b + a * x0)))
pgg[[1]] <- g + geom_point(mapping = aes(y = 1/(1 + exp(-(b + a * x0)))), pch = 2, size = 1, col = "blue")
pgg[[2]] <- glmg + geom_point(mapping = aes(x = x0, y = 1/(1 + exp(-(b + a * x0)))), pch = 2, size = 1, col = "blue")
# 青色三角が推定された回帰係数による成功確率。
ggpubr::as_ggplot(arrangeGrob(grobs = pgg, ncol = 2)) [1] 0.009710371 0.022909988 0.053090345 0.118218321 0.242758666 0.433934302
[7] 0.647023287 0.814236635 0.912900409 0.961630662 0.983587591# オッズ
# x = 5の場合
x <- 5
p1 <- 1/(1 + exp(-(b + a * x)))
p1
p1/(1 - p1)[1] 0.4339343
[1] 0.7665794# x = (5 + 1)の場合(xを1だけ増加させた場合)
x <- x + 1
p2 <- 1/(1 + exp(-(b + a * x)))
p2
p2/(1 - p2)[1] 0.6470233
[1] 1.833048# オッズ比
odds_ratio <- {
p2/(1 - p2)/(p1/(1 - p1))
} %>%
signif(signifdigits)
odds_ratio[1] 2.391204xが1だけ増加するとオッズは2.391204倍。
# 検算
{
exp(a) %>%
signif(signifdigits)
}
odds_ratio
# 係数aの指数関数はオッズ比と一致。[1] 2.391204
[1] 2.391204# 同じことですが対数オッズ比で検算。
log_odds_ratio <- log(odds_ratio) %>%
signif(signifdigits)
log_odds_ratio
a
# オッズ比の自然対数は係数aに一致。[1] 0.871797
[1] 0.8717972参考引用資料
最終更新
Sys.time()[1] "2024-04-23 08:44:32 JST"R、Quarto、Package
R.Version()$version.string[1] "R version 4.3.3 (2024-02-29 ucrt)"quarto::quarto_version()[1] '1.4.553'packageVersion(pkg = "tidyverse")[1] '2.0.0'