library(dplyr)
library(ggplot2)
func_sim_arma <- function(p,q,n,a_min,a_max,b_min,b_max){
x <- vector()
# 係数
a <- seq(a_min,a_max,0.001) %>% sample(size = p) %>% round(3);a
b <- seq(b_min,b_max,0.001) %>% sample(size = q) %>% round(3);b
# 撹乱項
epsilon <- rnorm(n);epsilon
# x初期値
x[1:max(p,q)] <- epsilon[1:max(p,q)]
for(i in (max(p,q)+1):n){
x[i] <- a %*% x[i-1:p] + b %*% epsilon[i-1:q] + epsilon[i]
}
return(list(a = a,b = b,epsilon = epsilon,x = x))
}Rで時系列分析:自己回帰移動平均モデル ARMA(p,q)
Rでデータサイエンス
ARMA(p,q)
自己回帰移動平均モデル
\[ y_t=c+\phi_1y_{t-1}+\phi_2y_{t-2}+\cdots+\phi_py_{t-p}+\epsilon_t+\theta_1\epsilon_{t-1}+\theta_2\epsilon_{t-2}+\cdots+\theta_q\epsilon_{t-q} \]
参考引用資料
- 加藤久和(2012),『gretlで計量経済分析』,日本評論社,pp.134-136
ARMAモデルのシミュレーション
# ラグ次数
p <- 2
q <- 1
# サンプルサイズ
n <- 100
# 係数aの下限
a_min <- -0.5
# 係数aの上限
a_max <- 0.5
# 係数bの下限
b_min <- -0.5
# 係数bの上限
b_max <- 0.5
result <- func_sim_arma(p = p,q = q,n = n,a_min = a_min,a_max = a_max,b_min = b_min,b_max = b_max)
a <- result$a#;a
b <- result$b#;b
ep <- result$epsilon
x <- result$x#;head(x)
df <- data.frame(n = seq(length(x)),x = x)
colnames(df)[2] <- paste0('a = ',paste0(a,collapse = ','),' , b = ',paste0(b,collapse = ','))#;head(df)
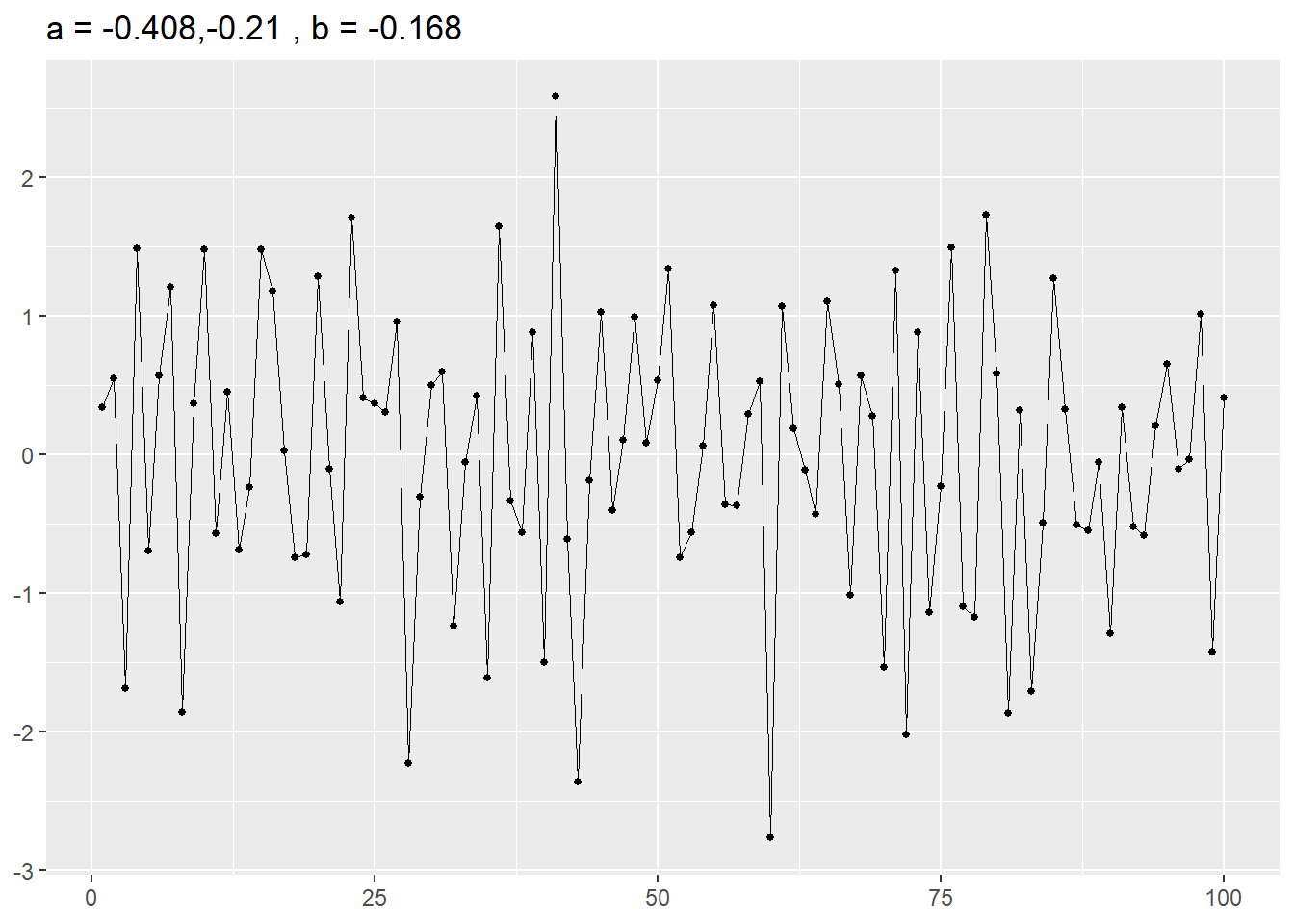
ggplot(mapping = aes(x = df[,1],y = df[,2])) + geom_line(size = 0.1) + geom_point(size = 1) +
theme(axis.title = element_blank()) + labs(title = colnames(df)[2])参考引用資料
最終更新
Sys.time()[1] "2024-04-27 06:40:20 JST"R、Quarto、Package
R.Version()$version.string[1] "R version 4.3.3 (2024-02-29 ucrt)"quarto::quarto_version()[1] '1.4.553'packageVersion(pkg = "tidyverse")[1] '2.0.0'