日次経済金融指標の計量分析
- 日経平均株価vs東京市場ドル円レート、ダウ平均株価vs日経平均株価、空売り比率vs日経平均株価、ドル円レートvs日経平均株価(月中平均、ベイズ推定)、トランプ大統領の就任前後における日経平均前営業日比ボラティリティの比較 -
アセット・マネジメント・コンサルティング株式会社 https://am-consulting.co.jp
更新日時:2019-12-25 14:06:00
Analysis
日経平均株価と東京市場ドル円レート(Source:日本銀行,日本経済新聞社) ダウ平均株価と日経平均株価(Source:Yahoo Finance,FRED,日本経済新聞社) 空売り比率と日経平均株価(Source:日本取引所グループ、日本経済新聞社) ドル円レートと日経平均株価:ベイズ推定:線形回帰モデル トランプ大統領の就任前後における日経平均前営業日比ボラティリティの比較
日経平均株価と東京市場ドル円レート(Source:日本銀行,日本経済新聞社)
[1] "USDJPY"
Date Open High Low Close Center Index CloseToOpen HighToLow MA25 DeviationRate Close:Diff(lag=1) Close:Ratio(lag=1)
56 2019-12-04 108.68 108.67 108.43 108.48 108.55 104.80 -0.184 0.221 108.8936 -0.38 -0.62 -0.568
57 2019-12-05 108.84 108.93 108.78 108.89 108.86 104.78 0.046 0.138 108.8948 0.00 0.41 0.378
58 2019-12-06 108.73 108.78 108.66 108.67 108.78 104.94 -0.055 0.110 108.8972 -0.21 -0.22 -0.202
59 2019-12-09 108.64 108.66 108.55 108.57 108.58 104.98 -0.064 0.101 108.9216 -0.32 -0.10 -0.092
60 2019-12-10 108.59 108.66 108.57 108.63 108.64 104.75 0.037 0.083 108.9152 -0.26 0.06 0.055
61 2019-12-11 108.78 108.86 108.67 108.73 108.74 104.82 -0.046 0.175 108.9052 -0.16 0.10 0.092
62 2019-12-12 108.56 108.65 108.46 108.65 108.58 103.63 0.083 0.175 108.8928 -0.22 -0.08 -0.074
63 2019-12-13 109.40 109.66 108.84 109.63 109.50 103.59 0.210 0.753 108.9064 0.66 0.98 0.902
64 2019-12-16 109.39 109.44 109.30 109.41 109.39 103.35 0.018 0.128 108.9244 0.45 -0.22 -0.201
65 2019-12-17 109.58 109.62 109.49 109.60 109.54 103.47 0.018 0.119 108.9388 0.61 0.19 0.174
66 2019-12-18 109.53 109.57 109.42 109.44 109.44 103.47 -0.082 0.137 108.9536 0.45 -0.16 -0.146
67 2019-12-19 109.55 109.72 109.55 109.58 109.58 103.62 0.027 0.155 108.9868 0.54 0.14 0.128
68 2019-12-20 109.39 109.40 109.26 109.37 109.39 103.61 -0.018 0.128 109.0192 0.32 -0.21 -0.192
69 2019-12-23 109.50 109.54 109.37 109.40 109.42 103.69 -0.091 0.155 109.0384 0.33 0.03 0.027
70 2019-12-24 109.40 109.45 109.37 109.40 109.40 NA 0.000 0.073 109.0676 0.30 0.00 0.000[1] "NIKKEI"
Date Open High Low Close CloseToOpen HighToLow MA25 DeviationRate Close:Diff(lag=1) Close:Ratio(lag=1)
56 2019-12-04 23186.74 23203.77 23044.78 23135.23 -0.222 0.690 23255.06 -0.52 -244.58 -1.046
57 2019-12-05 23292.70 23363.44 23259.82 23300.09 0.032 0.445 23273.34 0.11 164.86 0.713
58 2019-12-06 23347.67 23412.48 23338.40 23354.40 0.029 0.317 23290.43 0.27 54.31 0.233
59 2019-12-09 23544.31 23544.31 23360.01 23430.70 -0.483 0.789 23313.63 0.50 76.30 0.327
60 2019-12-10 23372.39 23449.47 23336.93 23410.19 0.162 0.482 23319.96 0.39 -20.51 -0.088
61 2019-12-11 23421.14 23438.43 23333.63 23391.86 -0.125 0.449 23323.48 0.29 -18.33 -0.078
62 2019-12-12 23449.28 23468.15 23360.43 23424.81 -0.104 0.461 23327.26 0.42 32.95 0.141
63 2019-12-13 23810.56 24050.04 23775.73 24023.10 0.893 1.154 23352.51 2.87 598.29 2.554
64 2019-12-16 23955.20 24036.30 23950.05 23952.35 -0.012 0.360 23377.33 2.46 -70.75 -0.295
65 2019-12-17 24091.12 24091.12 23996.51 24066.12 -0.104 0.394 23399.17 2.85 113.77 0.475
66 2019-12-18 24023.27 24046.09 23919.36 23934.43 -0.370 0.530 23423.75 2.18 -131.69 -0.547
67 2019-12-19 23911.46 23945.53 23835.29 23864.85 -0.195 0.463 23452.69 1.76 -69.58 -0.291
68 2019-12-20 23893.45 23908.77 23746.63 23816.63 -0.322 0.683 23473.22 1.46 -48.22 -0.202
69 2019-12-23 23921.29 23923.09 23810.82 23821.11 -0.419 0.472 23489.39 1.41 4.48 0.019
70 2019-12-24 23839.18 23853.56 23796.35 23830.58 -0.036 0.240 23510.91 1.36 9.47 0.040単位根検定・共和分検定
- CADFtest {CADFtest}
- ca.po {urca}
$USDJPY_CloseToOpen
ADF test
data: x
ADF(0) = -8.9544, p-value = 0.00000000251
alternative hypothesis: true delta is less than 0
sample estimates:
delta
-1.144612
$NIKKEI_CloseToOpen
ADF test
data: x
ADF(1) = -7.2235, p-value = 0.0000004772
alternative hypothesis: true delta is less than 0
sample estimates:
delta
-1.386642
########################################
# Phillips and Ouliaris Unit Root Test #
########################################
Test of type Pu
detrending of series none
Call:
lm(formula = z[, 1] ~ z[, -1] - 1)
Residuals:
Min 1Q Median 3Q Max
-0.18271 -0.04444 0.01570 0.08951 0.24238
Coefficients:
Estimate Std. Error t value Pr(>|t|)
z[, -1] 0.10416 0.03209 3.246 0.00193 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.09605 on 59 degrees of freedom
Multiple R-squared: 0.1515, Adjusted R-squared: 0.1372
F-statistic: 10.54 on 1 and 59 DF, p-value: 0.00193
Value of test-statistic is: 68.6696
Critical values of Pu are:
10pct 5pct 1pct
critical values 20.3933 25.9711 38.3413最小二乗法
- lm {stats}
- dwtest {lmtest}
- ks.test {stats}
- confint {stats}
- Box.test {stats}
- 切片項\(\neq0\)
MODEL INFO:
Observations: 60
Dependent Variable: USDJPY_CloseToOpen
Type: OLS linear regression
MODEL FIT:
F(1,58) = 10.31, p = 0.00
R2 = 0.15
Adj. R2 = 0.14
Standard errors: OLS
---------------------------------------------------------------
Est. 2.5% 97.5% t val. p
------------------------ ------ ------- ------- -------- ------
(Intercept) 0.01 -0.01 0.04 1.06 0.29
NIKKEI_CloseToOpen 0.10 0.04 0.17 3.21 0.00
---------------------------------------------------------------
Durbin-Watson test
data: OLS_Model
DW = 2.4114, p-value = 0.9467
alternative hypothesis: true autocorrelation is greater than 0
One-sample Kolmogorov-Smirnov test
data: ResidualsOLS
D = 0.084468, p-value = 0.7534
alternative hypothesis: two-sided 2.5 % 97.5 %
(Intercept) -0.01163023 0.03798747
NIKKEI_CloseToOpen 0.03878814 0.16717655
Box-Ljung test
data: ResidualsOLS
X-squared = 14.481, df = 10, p-value = 0.1522- 切片項\(=0\)
MODEL INFO:
Observations: 60
Dependent Variable: USDJPY_CloseToOpen
Type: OLS linear regression
MODEL FIT:
F(1,59) = 10.54, p = 0.00
R2 = 0.15
Adj. R2 = 0.14
Standard errors: OLS
--------------------------------------------------------------
Est. 2.5% 97.5% t val. p
------------------------ ------ ------ ------- -------- ------
NIKKEI_CloseToOpen 0.10 0.04 0.17 3.25 0.00
--------------------------------------------------------------
Durbin-Watson test
data: OLS_Model_no_intercept
DW = 2.3652, p-value = 0.9408
alternative hypothesis: true autocorrelation is greater than 0
One-sample Kolmogorov-Smirnov test
data: ResidualsOLS_no_intercept
D = 0.13805, p-value = 0.1849
alternative hypothesis: two-sided 2.5 % 97.5 %
NIKKEI_CloseToOpen 0.03995344 0.1683613
Box-Ljung test
data: ResidualsOLS_no_intercept
X-squared = 14.587, df = 10, p-value = 0.1479一般化最小二乗法
- gls {nlme}
- corARMA {nlme}
- ks.test {stats}
- confint {stats}
- Box.test {stats}
- 残差の系列相関の有無に拘わらず一般化最小二乗法による回帰係数を求めています。
- 最小二乗法の残差に系列相関が見られない場合、ここではAR(\(p=0,q=0\))の結果(AIC最小)が表示されます。
- http://user.keio.ac.jp/~nagakura/zemi/GLS.pdf
- http://tokyox.matrix.jp/wiki/index.php?%E4%B8%80%E8%88%AC%E5%8C%96%E6%9C%80%E5%B0%8F%E4%BA%8C%E4%B9%97%E6%B3%95
- 切片項\(\neq0\)
Generalized least squares fit by REML
Model: USDJPY_CloseToOpen ~ NIKKEI_CloseToOpen
Data: USDJPY_NIKKEI
AIC BIC logLik
-96.3286 -86.02638 53.1643
Correlation Structure: ARMA(1,1)
Formula: ~1
Parameter estimate(s):
Phi1 Theta1
-0.8426918 0.6615541
Coefficients:
Value Std.Error t-value p-value
(Intercept) 0.01243702 0.01064200 1.168674 0.2473
NIKKEI_CloseToOpen 0.11609381 0.02898921 4.004726 0.0002
Correlation:
(Intr)
NIKKEI_CloseToOpen -0.037
Standardized residuals:
Min Q1 Med Q3 Max
-2.03575806 -0.54324309 0.03505838 0.78076549 2.35744431
Residual standard error: 0.09629237
Degrees of freedom: 60 total; 58 residual
One-sample Kolmogorov-Smirnov test
data: ResidualsGLS
D = 0.080139, p-value = 0.8063
alternative hypothesis: two-sided 2.5 % 97.5 %
(Intercept) -0.008420907 0.03329496
NIKKEI_CloseToOpen 0.059276016 0.17291161
Box-Ljung test
data: ResidualsGLS
X-squared = 15.627, df = 10, p-value = 0.1108- 切片項\(=0\)
Generalized least squares fit by REML
Model: USDJPY_CloseToOpen ~ NIKKEI_CloseToOpen - 1
Data: USDJPY_NIKKEI
AIC BIC logLik
-104.2126 -95.90245 56.1063
Correlation Structure: ARMA(1,1)
Formula: ~1
Parameter estimate(s):
Phi1 Theta1
-0.8464688 0.6655166
Coefficients:
Value Std.Error t-value p-value
NIKKEI_CloseToOpen 0.1174511 0.0290519 4.042804 0.0002
Standardized residuals:
Min Q1 Med Q3 Max
-1.8998827 -0.4070335 0.1609874 0.9135233 2.4730353
Residual standard error: 0.09668565
Degrees of freedom: 60 total; 59 residual
One-sample Kolmogorov-Smirnov test
data: ResidualsGLS_no_intercept
D = 0.12728, p-value = 0.2624
alternative hypothesis: two-sided 2.5 % 97.5 %
NIKKEI_CloseToOpen 0.06051046 0.1743918
Box-Ljung test
data: ResidualsGLS_no_intercept
X-squared = 15.739, df = 10, p-value = 0.1073散布図・QQプロット・残差の時系列推移
- (注意)線形回帰の傾き(\(a\))、切片(\(b\))それぞれの検定統計量、p値に関わらず\(y=ax+b\)とした回帰直線やその残差を散布図、QQプロット等にプロットしています。
- 散布図とQQプロット
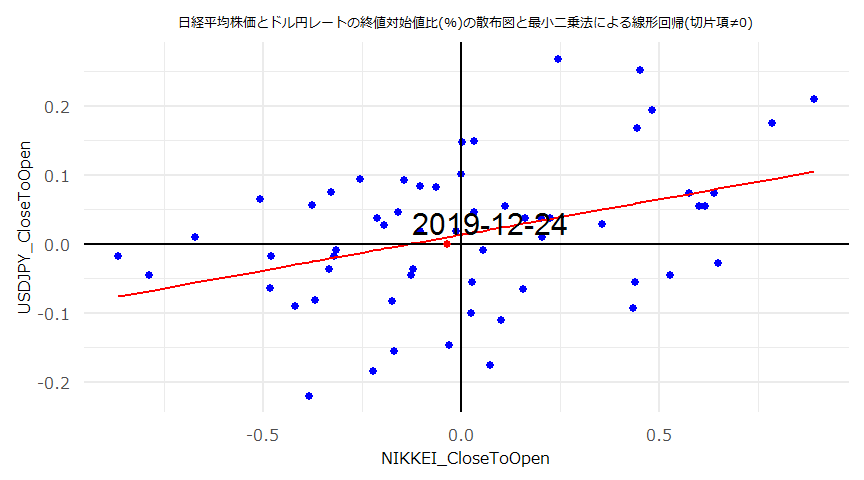
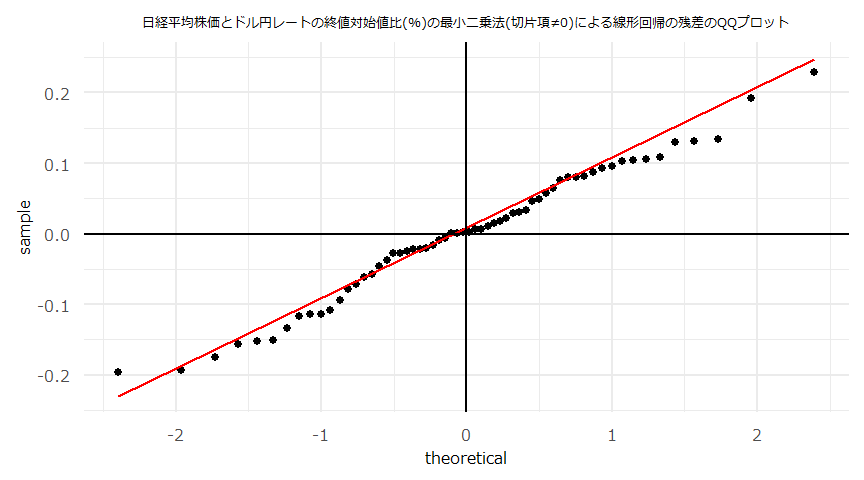
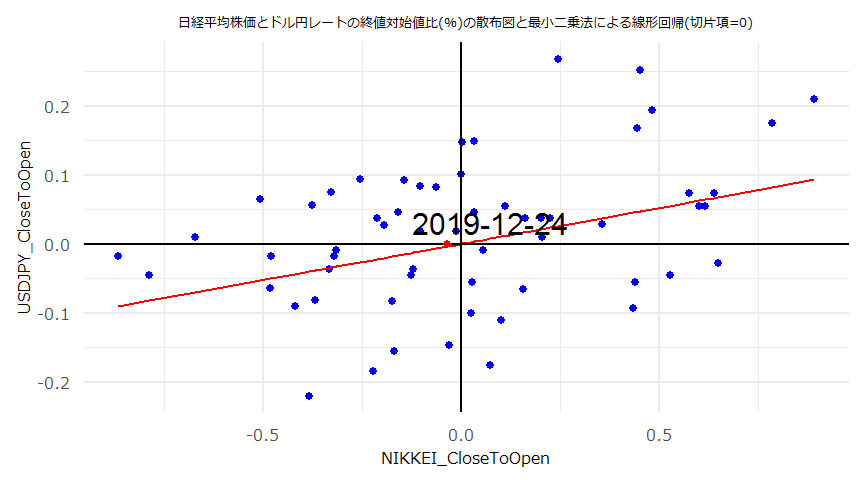
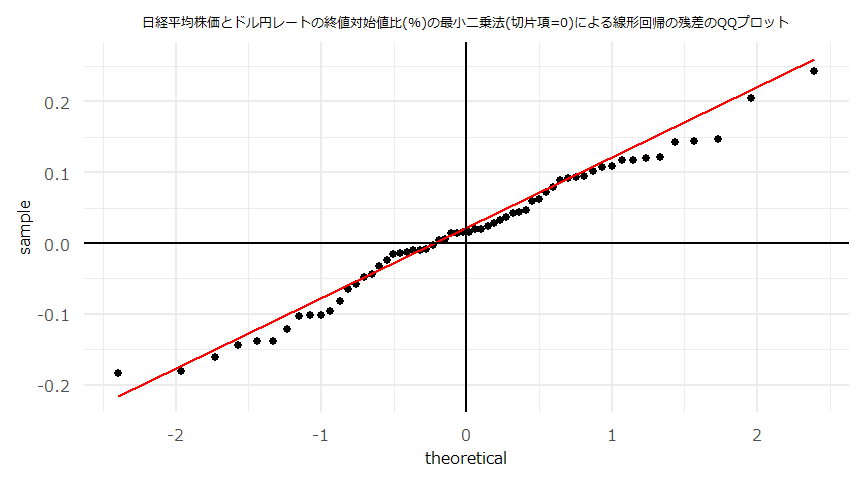
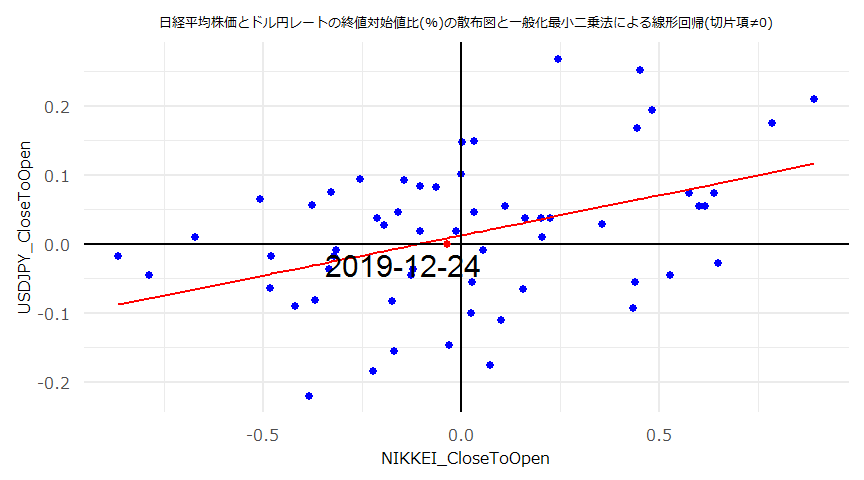
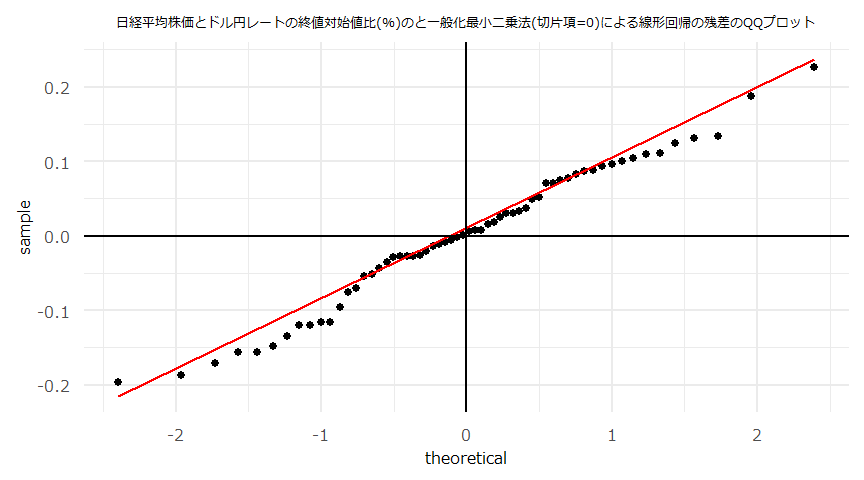
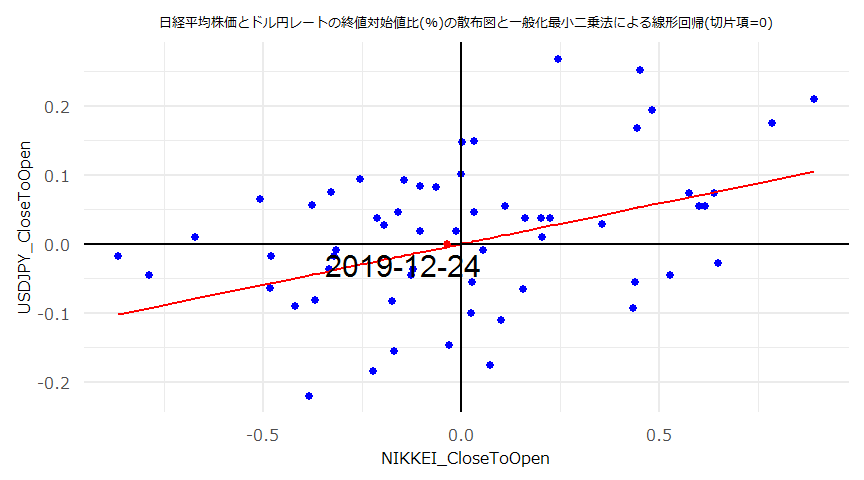
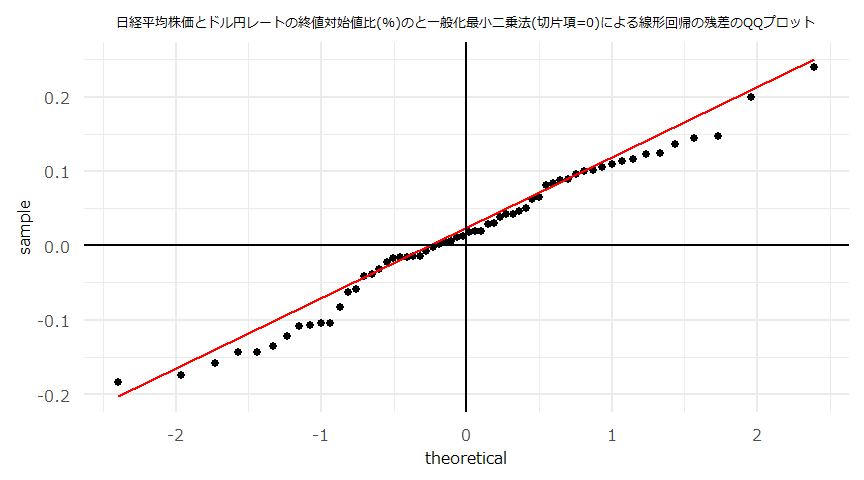
- 残差の自己相関(ACF)
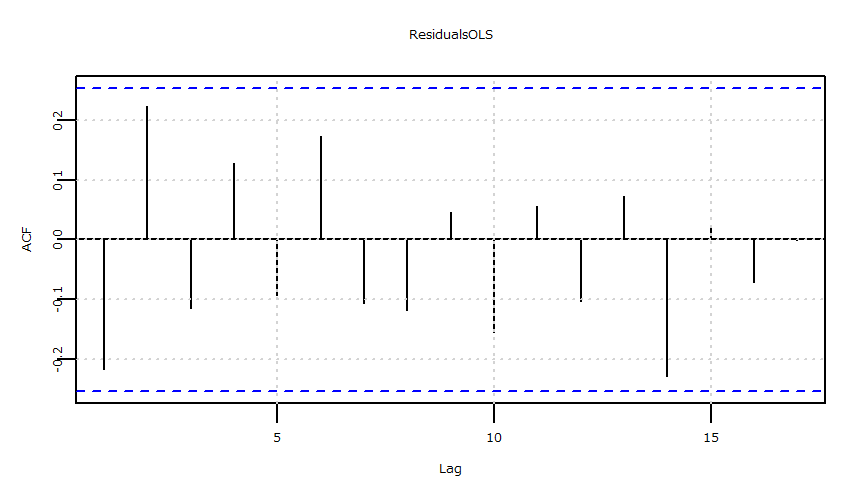
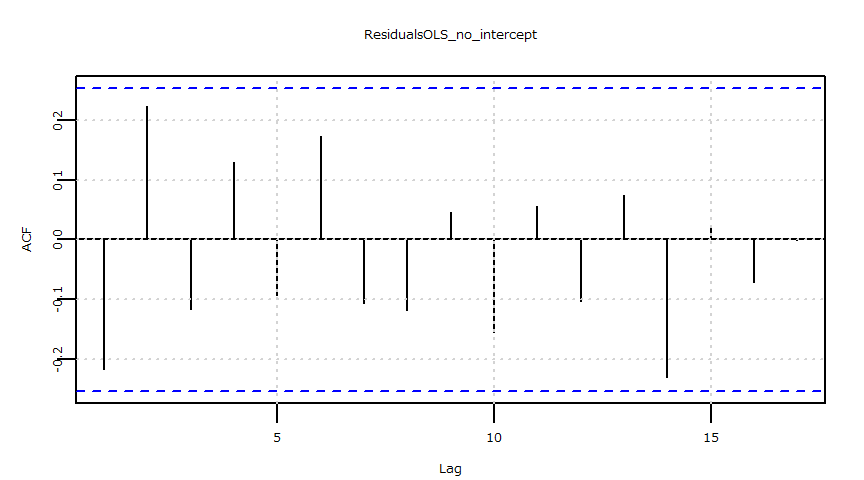
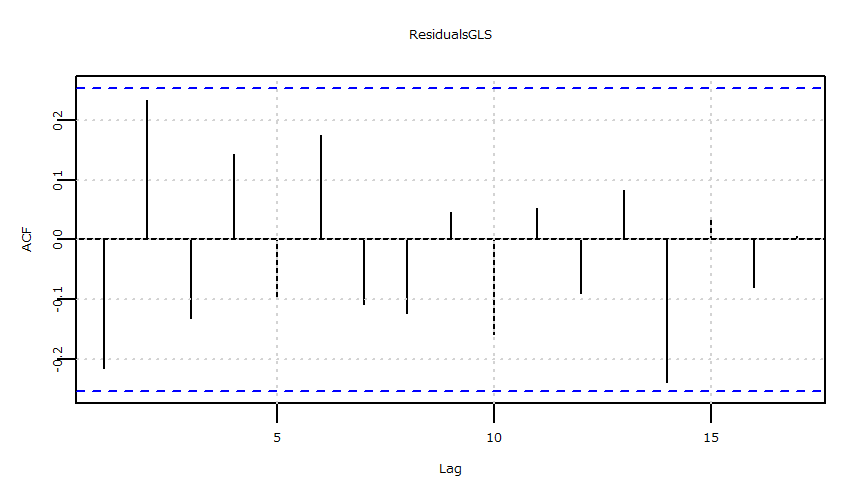
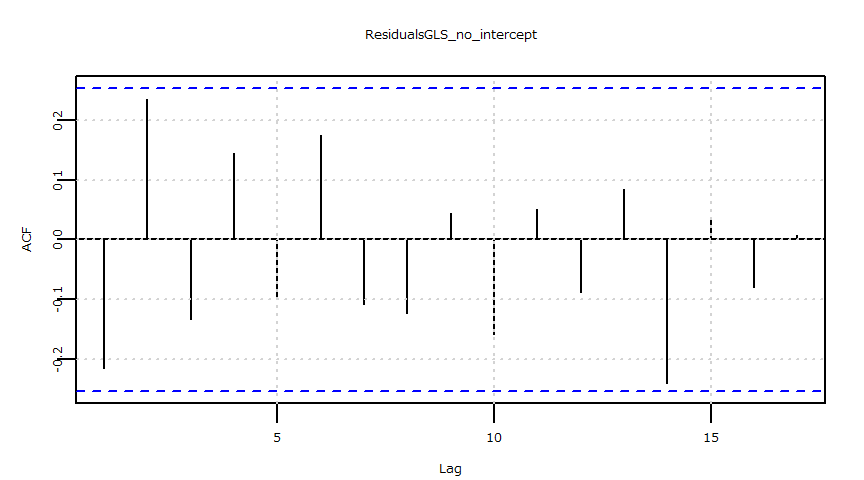
- 残差の自己相関(PACF)
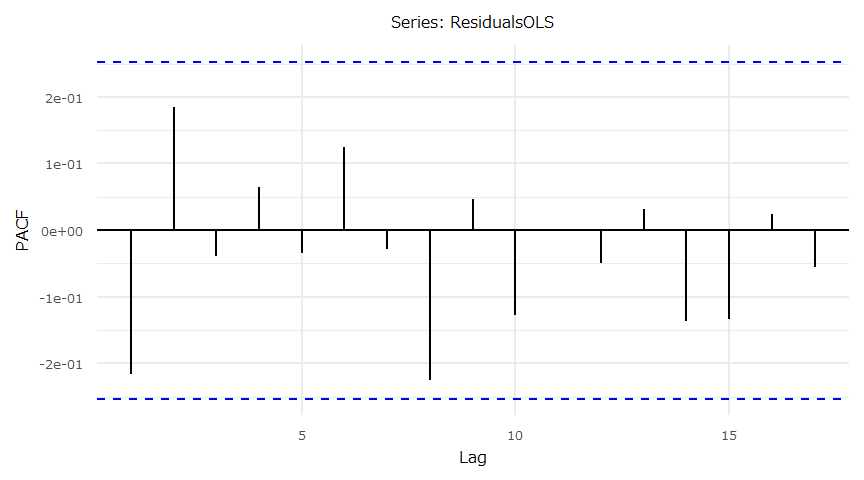
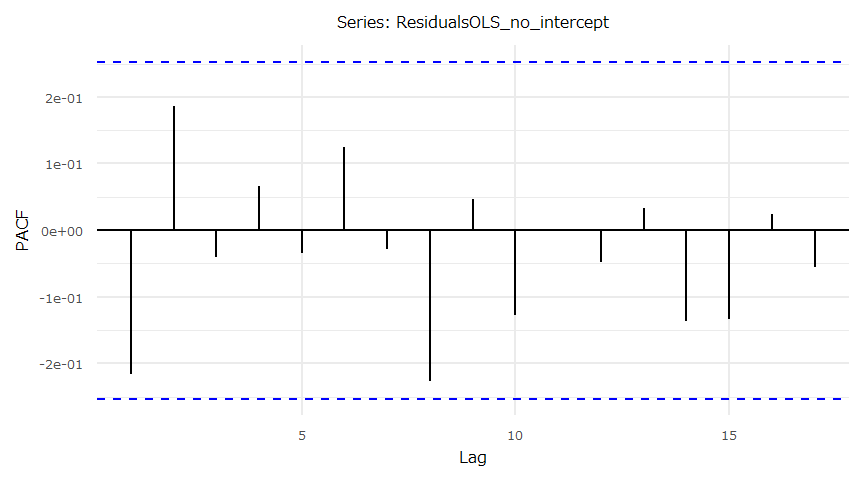
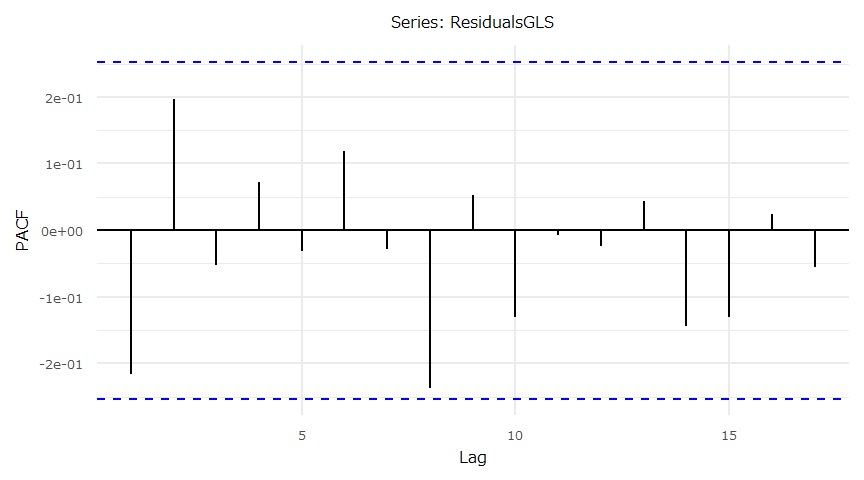
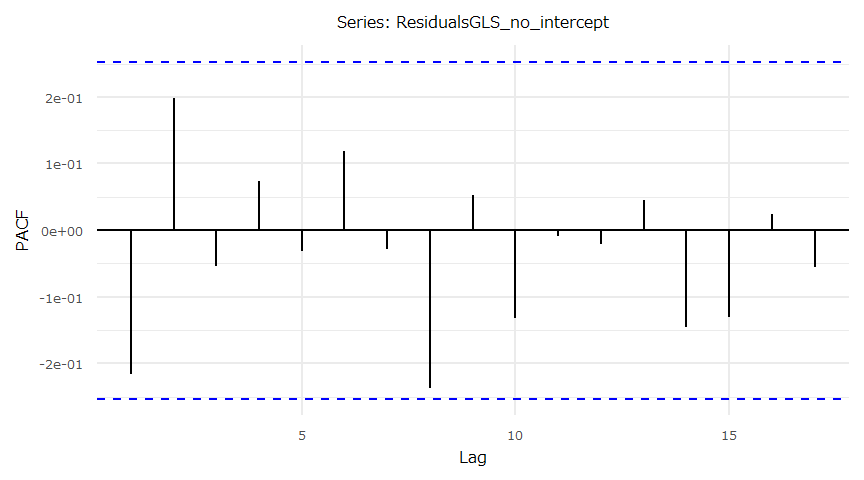
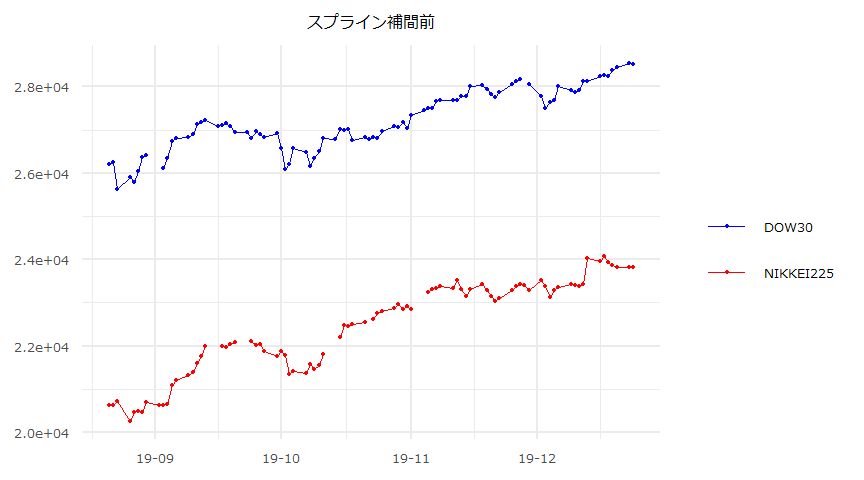
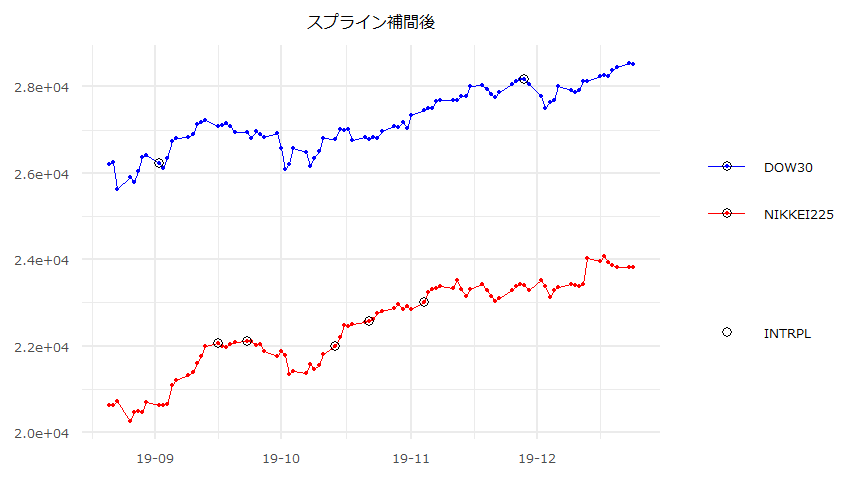
ダウ平均株価と日経平均株価(Source:Yahoo Finance,FRED,日本経済新聞社)
時系列チャート
- Source:
- (注意) 欠損値(休場日)は原系列にスプライン補間を掛けた上で前日比を算出している。
- 対象期間:2019-08-21~2019-12-24
- サンプルサイズ:n=90
単位根検定・共和分検定
- CADFtest {CADFtest}
- ca.po {urca}
単位根検定
$DOW30
ADF test
data: x
ADF(0) = -2.591, p-value = 0.2855
alternative hypothesis: true delta is less than 0
sample estimates:
delta
-0.1330281
$NIKKEI225
ADF test
data: x
ADF(0) = -2.0945, p-value = 0.5413
alternative hypothesis: true delta is less than 0
sample estimates:
delta
-0.1023453
$DOW30_Change
ADF test
data: x
ADF(2) = -7.2466, p-value = 0.00000009042
alternative hypothesis: true delta is less than 0
sample estimates:
delta
-1.282188
$NIKKEI225_Change
ADF test
data: x
ADF(0) = -9.1982, p-value = 0.00000000005683
alternative hypothesis: true delta is less than 0
sample estimates:
delta
-1.003339 共和分検定
[1] "DOW30 × NIKKEI225"
########################################
# Phillips and Ouliaris Unit Root Test #
########################################
Test of type Pu
detrending of series none
Call:
lm(formula = z[, 1] ~ z[, -1] - 1)
Residuals:
Min 1Q Median 3Q Max
-967.2 -484.4 -195.3 445.3 1575.1
Coefficients:
Estimate Std. Error t value Pr(>|t|)
z[, -1] 1.211440 0.003134 386.5 <0.0000000000000002 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 667.9 on 89 degrees of freedom
Multiple R-squared: 0.9994, Adjusted R-squared: 0.9994
F-statistic: 1.494e+05 on 1 and 89 DF, p-value: < 0.00000000000000022
Value of test-statistic is: 3.9619
Critical values of Pu are:
10pct 5pct 1pct
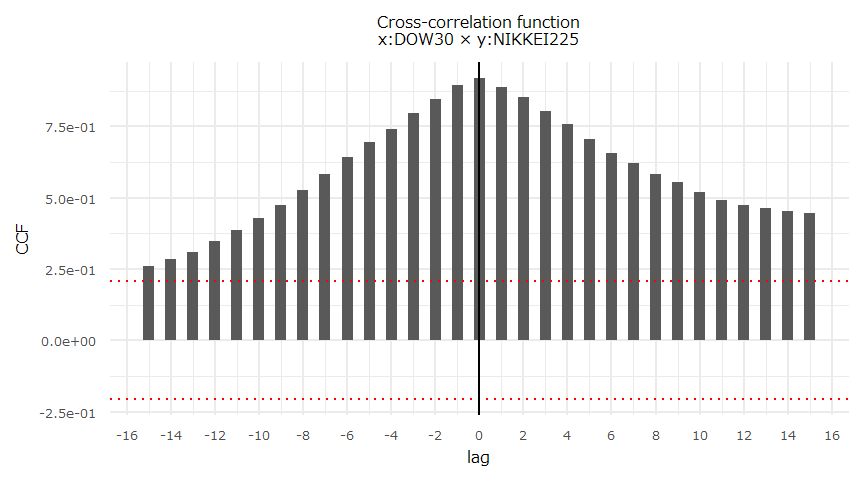
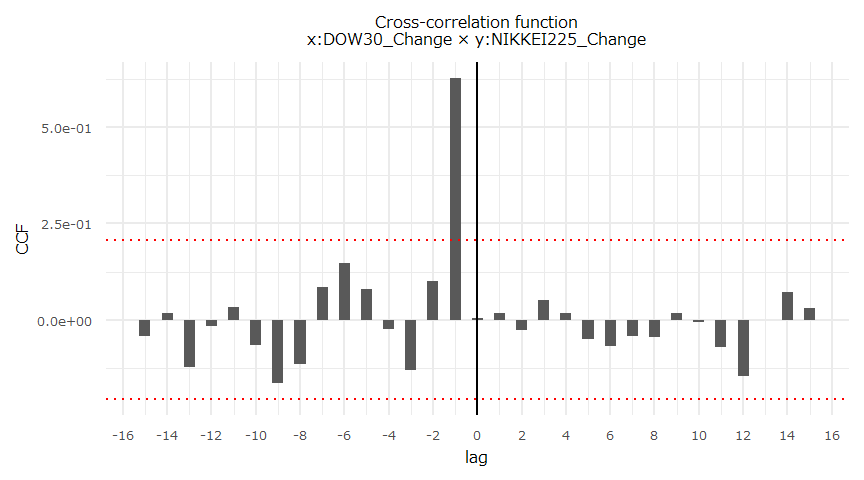
critical values 20.3933 25.9711 38.3413相互相関関数
- ggCcf {forecast}
ベクトル自己回帰モデル
- VARselect {vars}
- VAR {vars}
VAR Estimation Results:
=========================
Endogenous variables: DOW30, NIKKEI225
Deterministic variables: const
Sample size: 89
Log Likelihood: -1151.782
Roots of the characteristic polynomial:
0.9886 0.7546
Call:
VAR(y = obj, p = selected_lag, type = "const")
Estimation results for equation DOW30:
======================================
DOW30 = DOW30.l1 + NIKKEI225.l1 + const
Estimate Std. Error t value Pr(>|t|)
DOW30.l1 0.88230 0.06605 13.358 <0.0000000000000002 ***
NIKKEI225.l1 0.07046 0.04500 1.566 0.121
const 1647.32153 957.73430 1.720 0.089 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 173.7 on 86 degrees of freedom
Multiple R-Squared: 0.942, Adjusted R-squared: 0.9406
F-statistic: 698 on 2 and 86 DF, p-value: < 0.00000000000000022
Estimation results for equation NIKKEI225:
==========================================
NIKKEI225 = DOW30.l1 + NIKKEI225.l1 + const
Estimate Std. Error t value Pr(>|t|)
DOW30.l1 0.19275 0.05558 3.468 0.000821 ***
NIKKEI225.l1 0.86088 0.03786 22.737 < 0.0000000000000002 ***
const -2086.44362 805.89249 -2.589 0.011302 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 146.1 on 86 degrees of freedom
Multiple R-Squared: 0.9803, Adjusted R-squared: 0.9799
F-statistic: 2145 on 2 and 86 DF, p-value: < 0.00000000000000022
Covariance matrix of residuals:
DOW30 NIKKEI225
DOW30 30165 2271
NIKKEI225 2271 21358
Correlation matrix of residuals:
DOW30 NIKKEI225
DOW30 1.00000 0.08945
NIKKEI225 0.08945 1.00000
VAR Estimation Results:
=========================
Endogenous variables: DOW30_Change, NIKKEI225_Change
Deterministic variables: const
Sample size: 89
Log Likelihood: -159.944
Roots of the characteristic polynomial:
0.1094 0.09431
Call:
VAR(y = obj, p = selected_lag, type = "const")
Estimation results for equation DOW30_Change:
=============================================
DOW30_Change = DOW30_Change.l1 + NIKKEI225_Change.l1 + const
Estimate Std. Error t value Pr(>|t|)
DOW30_Change.l1 0.01659 0.10692 0.155 0.877
NIKKEI225_Change.l1 0.01535 0.10015 0.153 0.879
const 0.09291 0.07289 1.275 0.206
Residual standard error: 0.6615 on 86 degrees of freedom
Multiple R-Squared: 0.0005554, Adjusted R-squared: -0.02269
F-statistic: 0.0239 on 2 and 86 DF, p-value: 0.9764
Estimation results for equation NIKKEI225_Change:
=================================================
NIKKEI225_Change = DOW30_Change.l1 + NIKKEI225_Change.l1 + const
Estimate Std. Error t value Pr(>|t|)
DOW30_Change.l1 0.670169 0.089309 7.504 0.0000000000527 ***
NIKKEI225_Change.l1 -0.001546 0.083650 -0.018 0.985
const 0.092429 0.060883 1.518 0.133
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.5525 on 86 degrees of freedom
Multiple R-Squared: 0.3957, Adjusted R-squared: 0.3816
F-statistic: 28.15 on 2 and 86 DF, p-value: 0.000000000393
Covariance matrix of residuals:
DOW30_Change NIKKEI225_Change
DOW30_Change 0.437596 0.001839
NIKKEI225_Change 0.001839 0.305302
Correlation matrix of residuals:
DOW30_Change NIKKEI225_Change
DOW30_Change 1.00000 0.00503
NIKKEI225_Change 0.00503 1.00000グレンジャー因果
- causality {vars}
Dow → Nikkei
Granger causality H0: DOW30_Change do not Granger-cause NIKKEI225_Change
data: VAR object var_result
F-Test = 56.309, df1 = 1, df2 = 172, p-value = 0.000000000003182Nikkei → Dow
Granger causality H0: NIKKEI225_Change do not Granger-cause DOW30_Change
data: VAR object var_result
F-Test = 0.023496, df1 = 1, df2 = 172, p-value = 0.8784インパルス応答
- irf {vars}
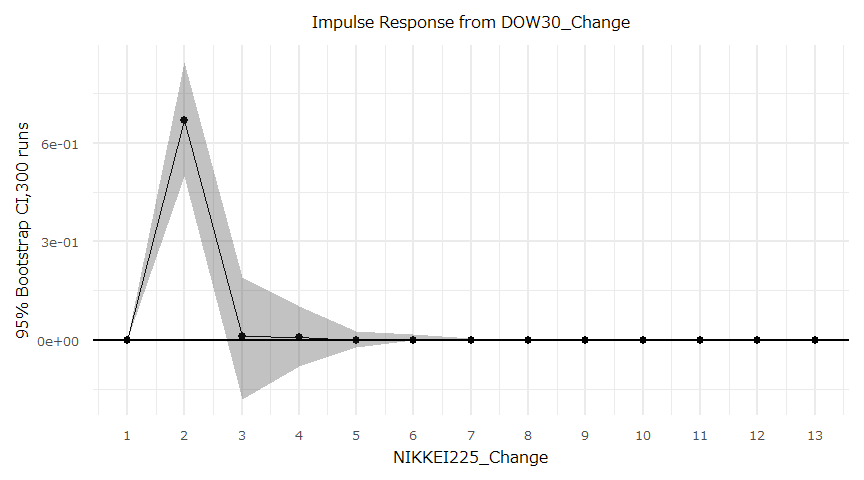
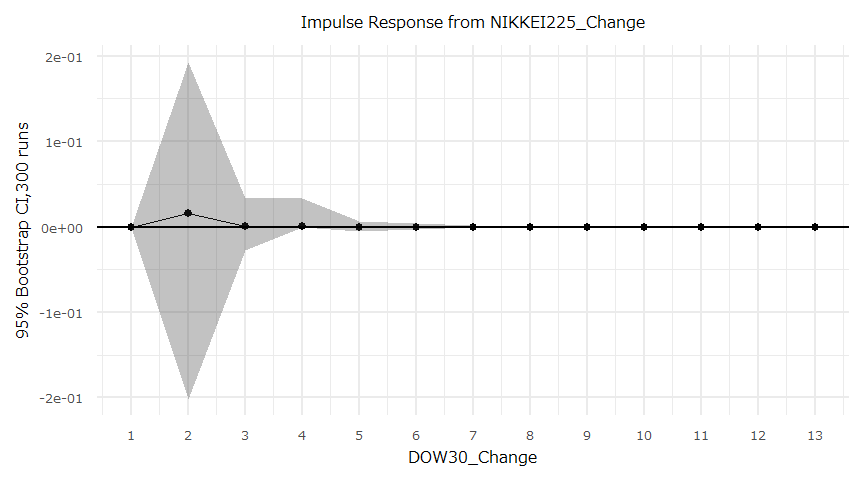
空売り比率と日経平均株価(Source:日本取引所グループ、日本経済新聞社)
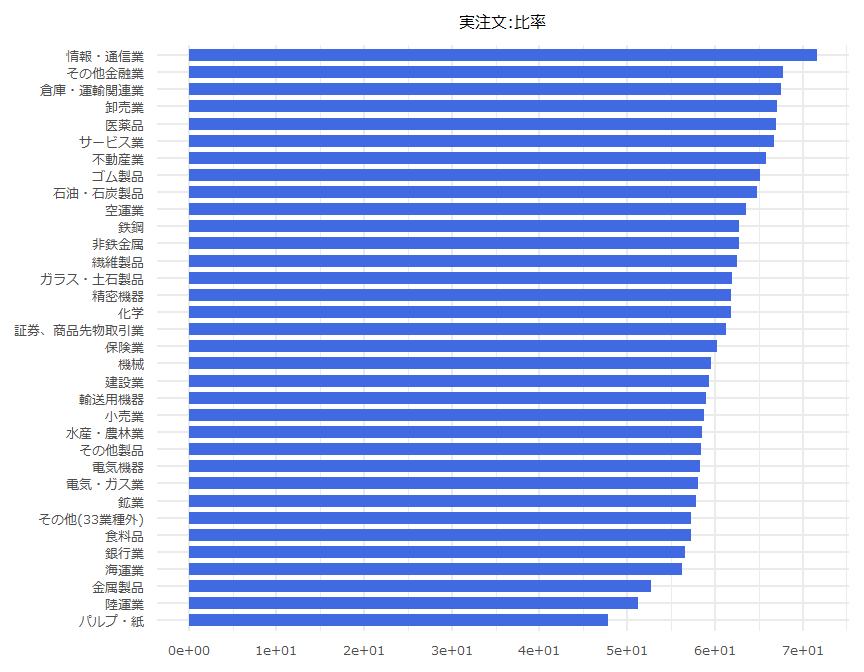
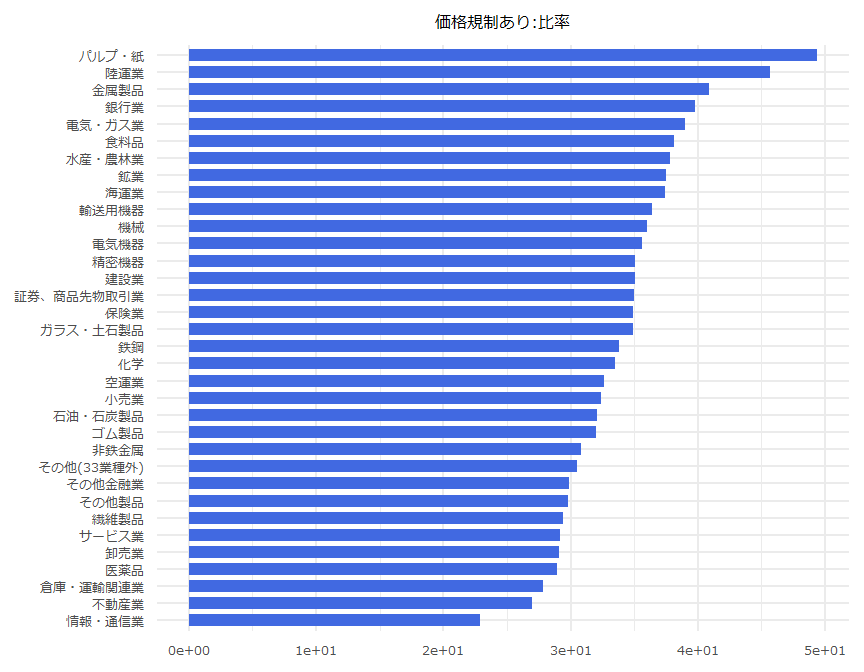
業種別空売り集計
- 2019年12月24日
- 「空売り合計:比率」は100から「実注文:比率」を減じた数値としています。
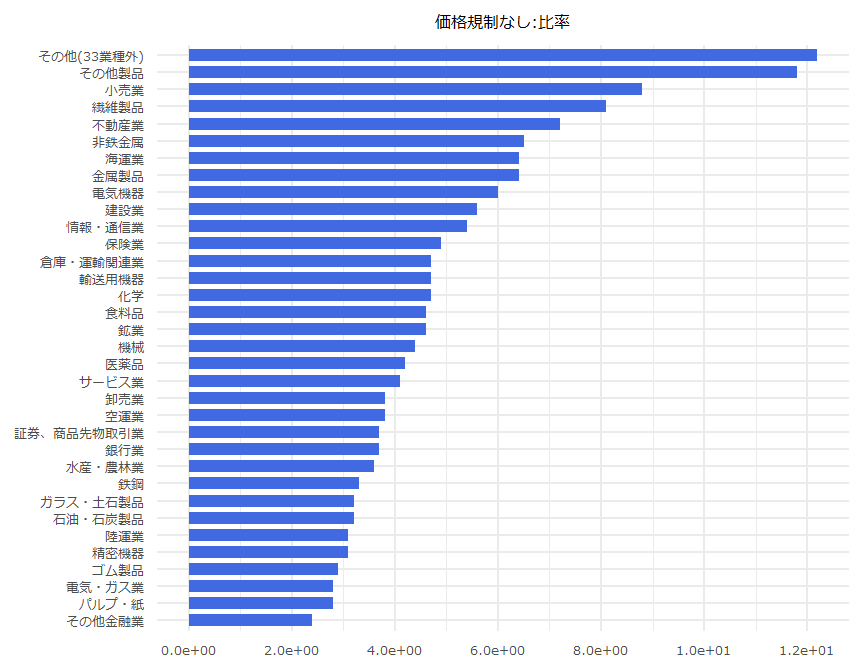
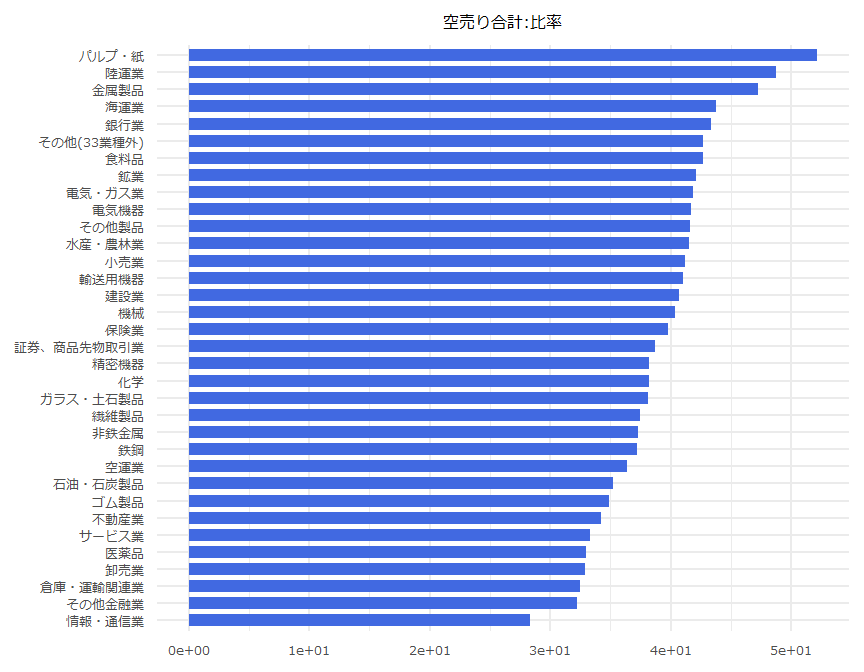
| N | 業種名 | 空売り合計:比率 |
|---|---|---|
| 1 | 水産・農林業 | 41.5 |
| 2 | 鉱業 | 42.1 |
| 3 | 建設業 | 40.7 |
| 4 | 食料品 | 42.7 |
| 5 | 繊維製品 | 37.5 |
| 6 | パルプ・紙 | 52.2 |
| 7 | 化学 | 38.2 |
| 8 | 医薬品 | 33 |
| 9 | 石油・石炭製品 | 35.2 |
| 10 | ゴム製品 | 34.9 |
| 11 | ガラス・土石製品 | 38.1 |
| 12 | 鉄鋼 | 37.2 |
| 13 | 非鉄金属 | 37.3 |
| 14 | 金属製品 | 47.3 |
| 15 | 機械 | 40.4 |
| 16 | 電気機器 | 41.7 |
| 17 | 輸送用機器 | 41 |
| 18 | 精密機器 | 38.2 |
| 19 | その他製品 | 41.6 |
| 20 | 電気・ガス業 | 41.9 |
| 21 | 陸運業 | 48.8 |
| 22 | 海運業 | 43.8 |
| 23 | 空運業 | 36.4 |
| 24 | 倉庫・運輸関連業 | 32.5 |
| 25 | 情報・通信業 | 28.3 |
| 26 | 卸売業 | 32.9 |
| 27 | 小売業 | 41.2 |
| 28 | 銀行業 | 43.4 |
| 29 | 証券、商品先物取引業 | 38.7 |
| 30 | 保険業 | 39.8 |
| 31 | その他金融業 | 32.2 |
| 32 | 不動産業 | 34.2 |
| 33 | サービス業 | 33.3 |
| 34 | その他(33業種外) | 42.7 |
空売り比率の時系列推移
- 2019-08-14 ~ 2019-12-24
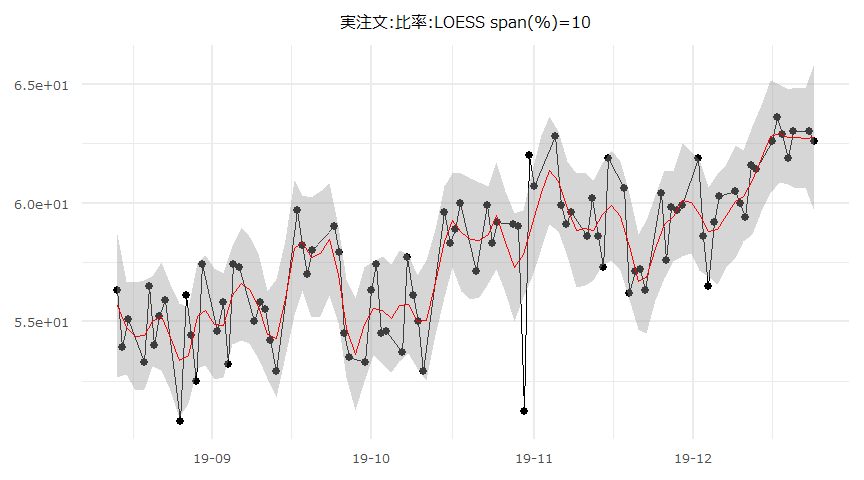
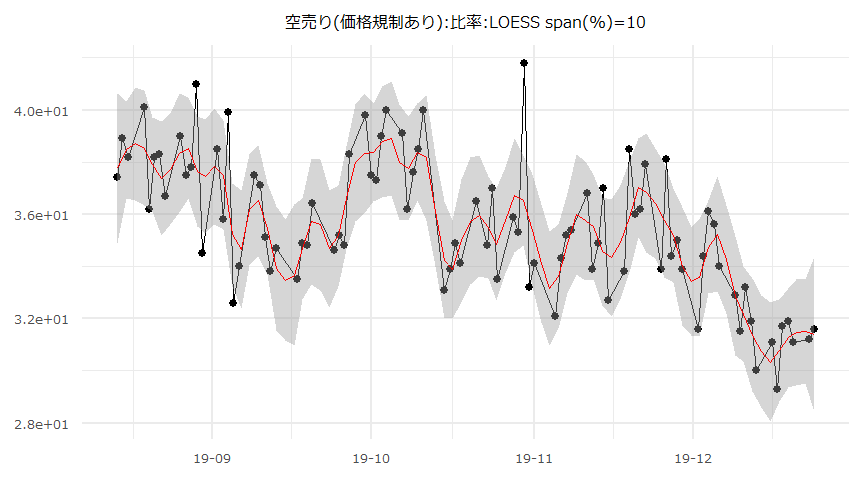
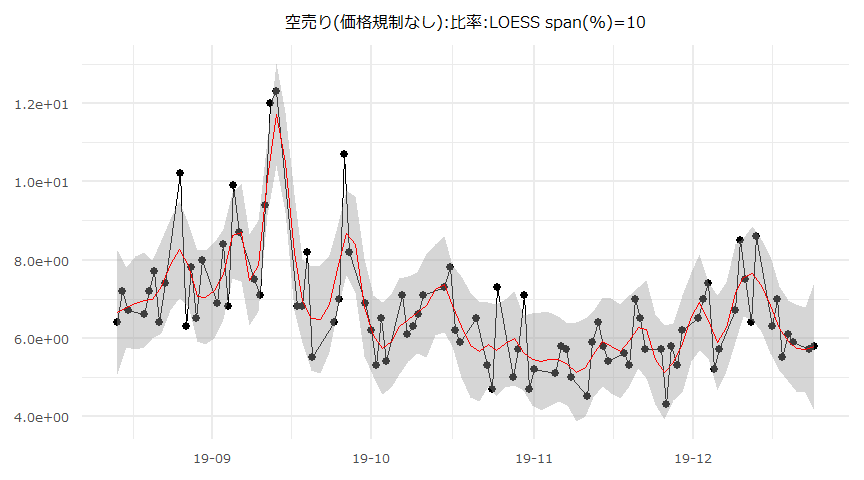
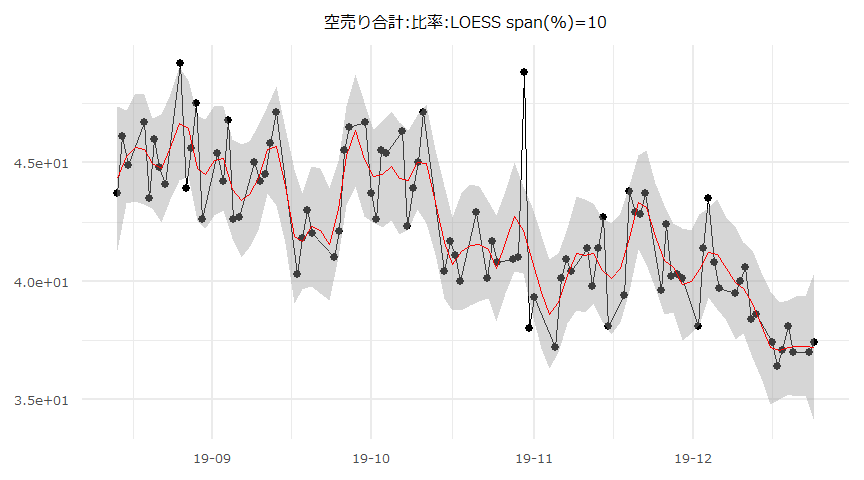
| Date | 12-24 | 12-23 | 12-20 | 12-19 | 12-18 | 12-17 | 12-16 | 12-13 |
|---|---|---|---|---|---|---|---|---|
| 実注文:比率 | 62.6 | 63 | 63 | 61.9 | 62.9 | 63.6 | 62.6 | 61.4 |
| 空売り(価格規制あり):比率 | 31.6 | 31.2 | 31.1 | 31.9 | 31.7 | 29.3 | 31.1 | 30 |
| 空売り(価格規制なし):比率 | 5.8 | 5.7 | 5.9 | 6.1 | 5.5 | 7 | 6.3 | 8.6 |
| 空売り合計:比率 | 37.4 | 37 | 37 | 38.1 | 37.1 | 36.4 | 37.4 | 38.6 |
日経平均株価と空売り比率
時系列推移
- 対象期間:2019-08-14 ~ 2019-12-24
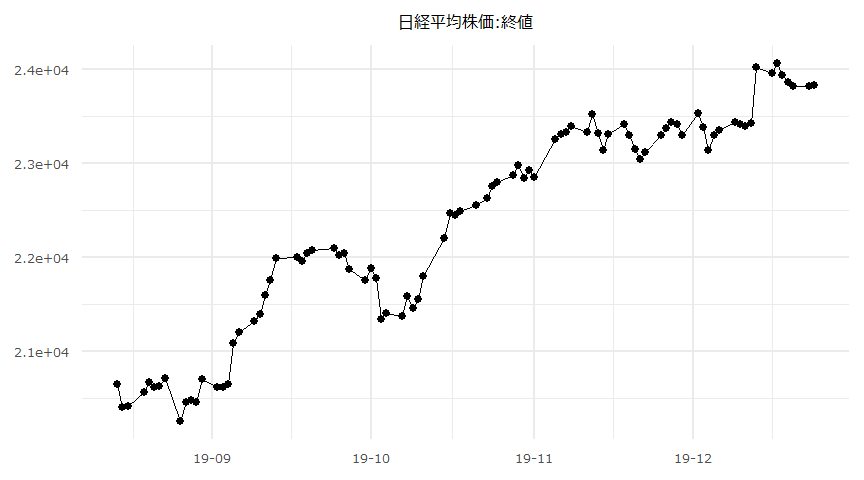
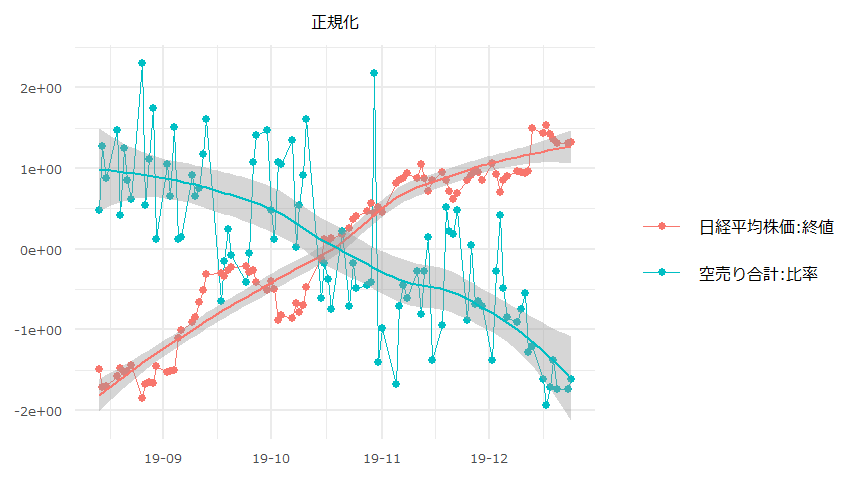
単位根検定/共和分検定
- CADFtest {CADFtest}
- ca.po {urca}
- 各系列の“_change“は前営業日との差。
- 対象期間: 2019-08-14 ~ 2019-12-24,90days
### 単位根検定 ###
$NIKKEI225.close
ADF test
data: x
ADF(0) = -2.1666, p-value = 0.5017
alternative hypothesis: true delta is less than 0
sample estimates:
delta
-0.1102726
$ShortSalerRatio
ADF test
data: x
ADF(0) = -7.9666, p-value = 0.000000005333
alternative hypothesis: true delta is less than 0
sample estimates:
delta
-0.8607999
$NIKKEI225.close_change
ADF test
data: x
ADF(0) = -9.1907, p-value = 0.00000000005833
alternative hypothesis: true delta is less than 0
sample estimates:
delta
-1.002416
$ShortSalerRatio_change
ADF test
data: x
ADF(2) = -8.8201, p-value = 0.0000000002165
alternative hypothesis: true delta is less than 0
sample estimates:
delta
-2.348904 ### 共和分検定 ###
########################################
# Phillips and Ouliaris Unit Root Test #
########################################
Test of type Pu
detrending of series none
Call:
lm(formula = z[, 1] ~ z[, -1] - 1)
Residuals:
Min 1Q Median 3Q Max
-5551.2 -2270.9 586.3 2250.0 4969.2
Coefficients:
Estimate Std. Error t value Pr(>|t|)
z[, -1] 524.640 6.377 82.28 <0.0000000000000002 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2562 on 89 degrees of freedom
Multiple R-squared: 0.987, Adjusted R-squared: 0.9869
F-statistic: 6769 on 1 and 89 DF, p-value: < 0.00000000000000022
Value of test-statistic is: 0.2996
Critical values of Pu are:
10pct 5pct 1pct
critical values 20.3933 25.9711 38.3413最小二乗法
- lm {stats}
- dwtest {lmtest}
- ks.test {stats}
- confint {stats}
- Box.test {stats}
- Ljung-Box 検定のラグは15としている。
- 対象期間: 2019-08-14 ~ 2019-12-24,90days
- 切片項\(\neq0\)
Call:
lm(formula = NIKKEI225.close_change ~ ShortSalerRatio_change,
data = datadf)
Residuals:
Min 1Q Median 3Q Max
-387.74 -70.73 -11.15 73.78 569.85
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 34.182 15.347 2.227 0.0285 *
ShortSalerRatio_change -28.729 5.653 -5.082 0.00000208 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 145.5 on 88 degrees of freedom
Multiple R-squared: 0.2269, Adjusted R-squared: 0.2181
F-statistic: 25.82 on 1 and 88 DF, p-value: 0.000002082
Durbin-Watson test
data: OLS_Model
DW = 1.88, p-value = 0.3013
alternative hypothesis: true autocorrelation is greater than 0
One-sample Kolmogorov-Smirnov test
data: ResidualsOLS
D = 0.079749, p-value = 0.588
alternative hypothesis: two-sided 2.5 % 97.5 %
(Intercept) 3.682693 64.68076
ShortSalerRatio_change -39.964450 -17.49417
Box-Ljung test
data: ResidualsOLS
X-squared = 11.949, df = 15, p-value = 0.6829- 切片項\(=0\)
Call:
lm(formula = NIKKEI225.close_change ~ ShortSalerRatio_change -
1, data = datadf)
Residuals:
Min 1Q Median 3Q Max
-352.00 -36.53 22.49 107.50 604.14
Coefficients:
Estimate Std. Error t value Pr(>|t|)
ShortSalerRatio_change -29.265 5.773 -5.07 0.00000215 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 148.7 on 89 degrees of freedom
Multiple R-squared: 0.2241, Adjusted R-squared: 0.2154
F-statistic: 25.7 on 1 and 89 DF, p-value: 0.000002151
Durbin-Watson test
data: OLS_Model_no_intercept
DW = 1.7822, p-value = 0.1892
alternative hypothesis: true autocorrelation is greater than 0
One-sample Kolmogorov-Smirnov test
data: ResidualsOLS_no_intercept
D = 0.16801, p-value = 0.01088
alternative hypothesis: two-sided 2.5 % 97.5 %
ShortSalerRatio_change -40.73552 -17.79511
Box-Ljung test
data: ResidualsOLS_no_intercept
X-squared = 11.895, df = 15, p-value = 0.687一般化最小二乗法
- gls {nlme}
- corARMA {nlme}
- ks.test {stats}
- confint {stats}
- Box.test {stats}
- 残差の系列相関の有無に拘わらず一般化最小二乗法による回帰係数を求めています。
- 最小二乗法の残差に系列相関が見られない場合、ここではAR(p=0,q=0)の結果(AIC最小)が表示されます。
- http://user.keio.ac.jp/~nagakura/zemi/GLS.pdf
- http://tokyox.matrix.jp/wiki/index.php?%E4%B8%80%E8%88%AC%E5%8C%96%E6%9C%80%E5%B0%8F%E4%BA%8C%E4%B9%97%E6%B3%95
- Ljung-Box 検定のラグは15としている。
- 切片項\(\neq0\)
Generalized least squares fit by REML
Model: NIKKEI225.close_change ~ ShortSalerRatio_change
Data: datadf
AIC BIC logLik
1143.194 1150.626 -568.5972
Coefficients:
Value Std.Error t-value p-value
(Intercept) 34.18172 15.347047 2.227251 0.0285
ShortSalerRatio_change -28.72931 5.653498 -5.081687 0.0000
Correlation:
(Intr)
ShortSalerRatio_change 0.043
Standardized residuals:
Min Q1 Med Q3 Max
-2.66553684 -0.48624141 -0.07665896 0.50723977 3.91752212
Residual standard error: 145.4629
Degrees of freedom: 90 total; 88 residual
One-sample Kolmogorov-Smirnov test
data: ResidualsGLS
D = 0.079749, p-value = 0.588
alternative hypothesis: two-sided 2.5 % 97.5 %
(Intercept) 4.102064 64.26138
ShortSalerRatio_change -39.809963 -17.64866
Box-Ljung test
data: ResidualsGLS
X-squared = 11.949, df = 15, p-value = 0.6829- 切片項\(=0\)
Generalized least squares fit by REML
Model: NIKKEI225.close_change ~ ShortSalerRatio_change - 1
Data: datadf
AIC BIC logLik
1153.369 1158.346 -574.6846
Coefficients:
Value Std.Error t-value p-value
ShortSalerRatio_change -29.26532 5.772687 -5.069618 0
Standardized residuals:
Min Q1 Med Q3 Max
-2.3677540 -0.2457028 0.1513119 0.7231028 4.0638061
Residual standard error: 148.6643
Degrees of freedom: 90 total; 89 residual
One-sample Kolmogorov-Smirnov test
data: ResidualsGLS_no_intercept
D = 0.16801, p-value = 0.01088
alternative hypothesis: two-sided 2.5 % 97.5 %
ShortSalerRatio_change -40.57957 -17.95106
Box-Ljung test
data: ResidualsGLS_no_intercept
X-squared = 11.895, df = 15, p-value = 0.687残差
- 時系列推移
- 自己相関
- 時系列推移
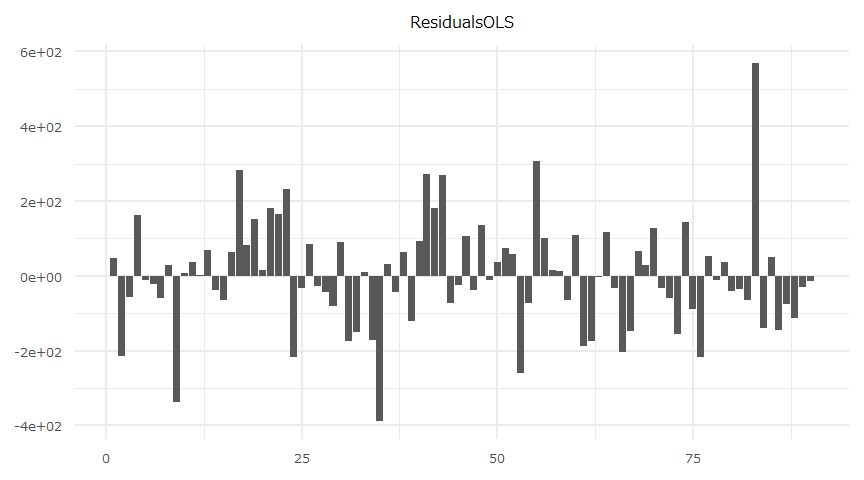
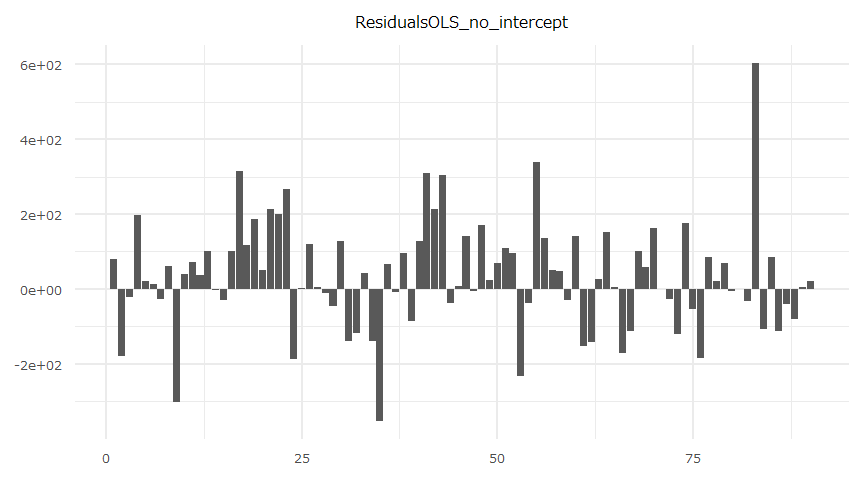
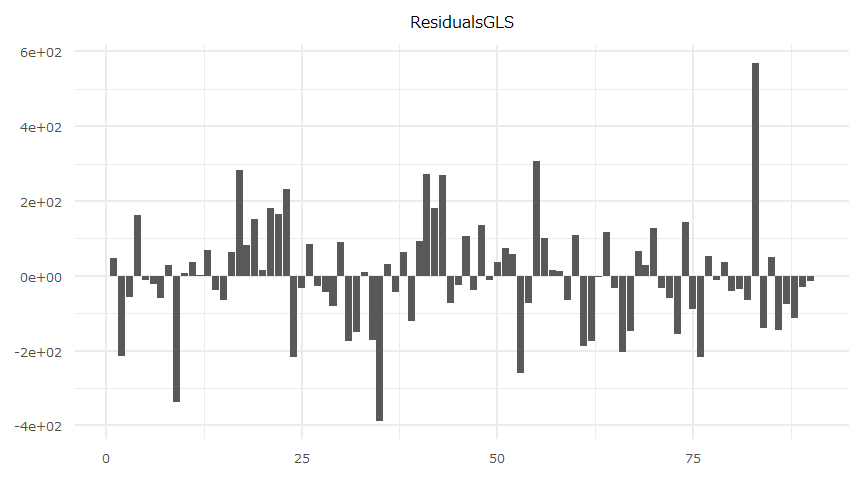
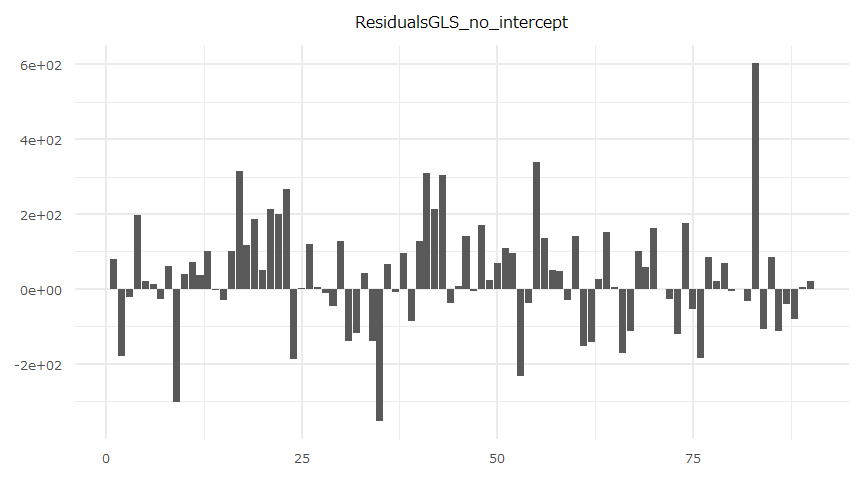
- 自己相関
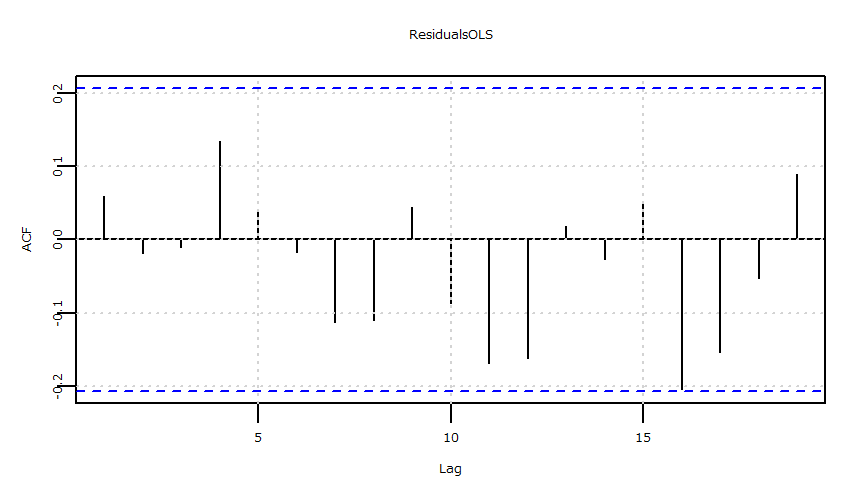
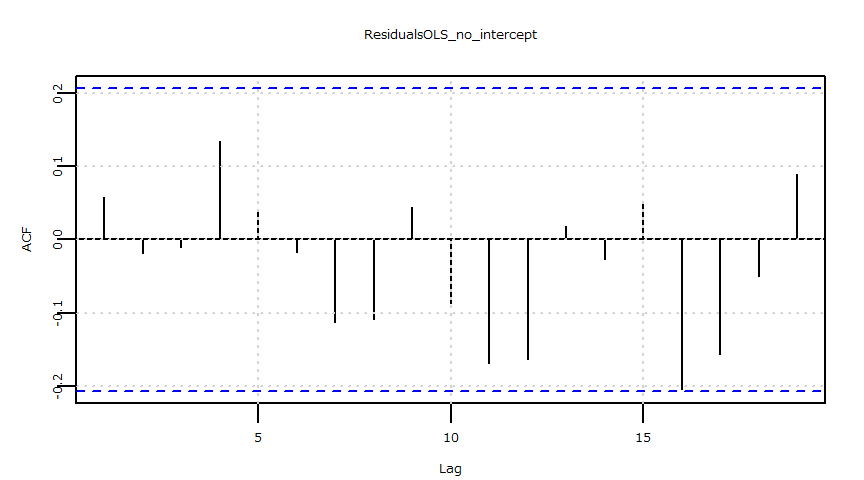
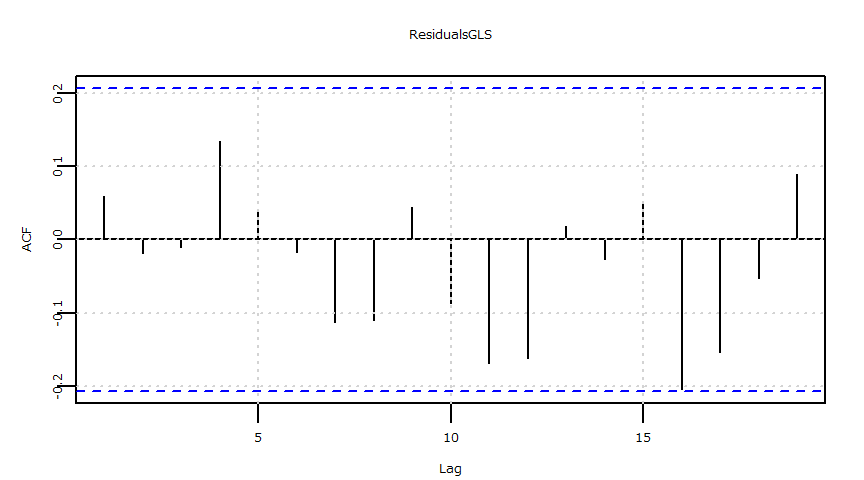
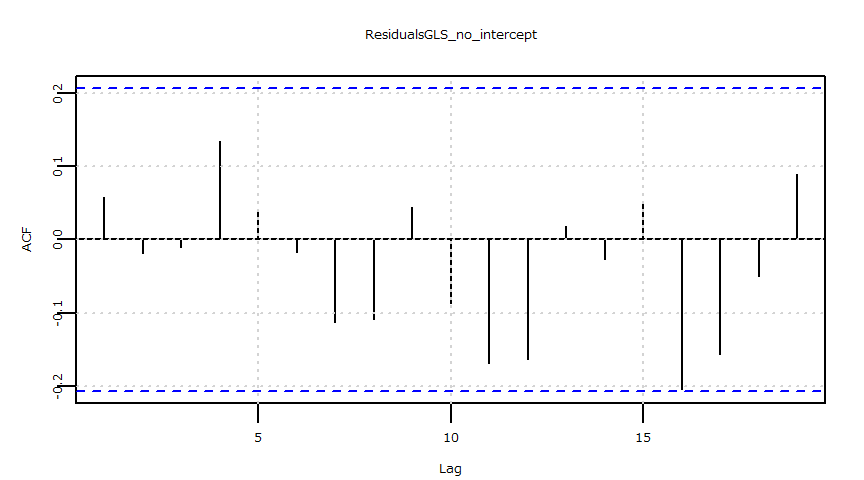
ドル円レートと日経平均株価:ベイズ推定:線形回帰モデル
\[\rm{NIKKEI}\sim\rm{Normal}(\beta_0 + \beta_1 \cdot \rm{USDJPY},\sigma)\]
# 数値はいずれも前月比(%)
head(df) Date NIKKEI USDJPY
13 2017-01-01 0.67 -1.05
14 2017-02-01 -0.03 -1.45
15 2017-03-01 0.79 -0.05
16 2017-04-01 -3.12 -2.59
17 2017-05-01 5.29 1.94
18 2017-06-01 1.62 -1.19tail(df) Date NIKKEI USDJPY
43 2019-07-01 2.53 0.15
44 2019-08-01 -4.46 -1.81
45 2019-09-01 4.63 1.06
46 2019-10-01 2.84 0.65
47 2019-11-01 4.87 0.69
48 2019-12-01 1.50 0.26apply(df[, -1], 2, adf.test)$NIKKEI
Augmented Dickey-Fuller Test
data: newX[, i]
Dickey-Fuller = -3.5875, Lag order = 3, p-value = 0.04791
alternative hypothesis: stationary
$USDJPY
Augmented Dickey-Fuller Test
data: newX[, i]
Dickey-Fuller = -4.1669, Lag order = 3, p-value = 0.01457
alternative hypothesis: stationary# 最尤推定
summary(lm(NIKKEI ~ USDJPY), confint = T, ci.width = 0.95)
Call:
lm(formula = NIKKEI ~ USDJPY)
Residuals:
Min 1Q Median 3Q Max
-4.7835 -1.1220 0.2934 1.2350 6.0612
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.8789 0.4230 2.078 0.0454 *
USDJPY 1.4584 0.2974 4.903 0.0000229 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.523 on 34 degrees of freedom
Multiple R-squared: 0.4142, Adjusted R-squared: 0.397
F-statistic: 24.04 on 1 and 34 DF, p-value: 0.00002293Gaussian <- "
data{
int N;
vector[N] NIKKEI;
vector[N] USDJPY;
}
parameters{
real beta0;
real beta1;
real <lower = 0> sigma;
}
model{
for(i in 1:N)
NIKKEI[i] ~ normal(beta0 + beta1*USDJPY[i], sigma);
}
generated quantities{
vector[N] pred_NIKKEI;
real log_lik[N];
for (i in 1:N){
pred_NIKKEI[i] = normal_rng(beta0 + beta1*USDJPY[i], sigma);
log_lik[i] = normal_lpdf(NIKKEI[i] | beta0 + beta1*USDJPY[i], sigma);
}
}
"datalist <- list(N = N, NIKKEI = NIKKEI, USDJPY = USDJPY)
iter <- 1400
warmup <- 400
chains <- 3
fit <- stan(model_code = Gaussian, data = datalist, iter = iter, warmup = warmup, thin = 1, chains = chains)
summary(fit)$summary[c("beta0", "beta1", "sigma"), ] mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
beta0 0.8875346 0.009630047 0.4428774 0.03346326 0.5973444 0.8823194 1.186767 1.786213 2114.999 1.0008931
beta1 1.4635474 0.005635220 0.2999310 0.87680494 1.2622379 1.4641785 1.659193 2.056325 2832.833 0.9997827
sigma 2.6145262 0.006997019 0.3353027 2.03981008 2.3895432 2.5752479 2.804797 3.363150 2296.402 1.0004320traceplot(fit) + theme(axis.text.x = element_text(size = 5), axis.text.y = element_text(size = 5), strip.text.x = element_text(size = 5), legend.title = element_text(size = 5), legend.text = element_text(size = 5))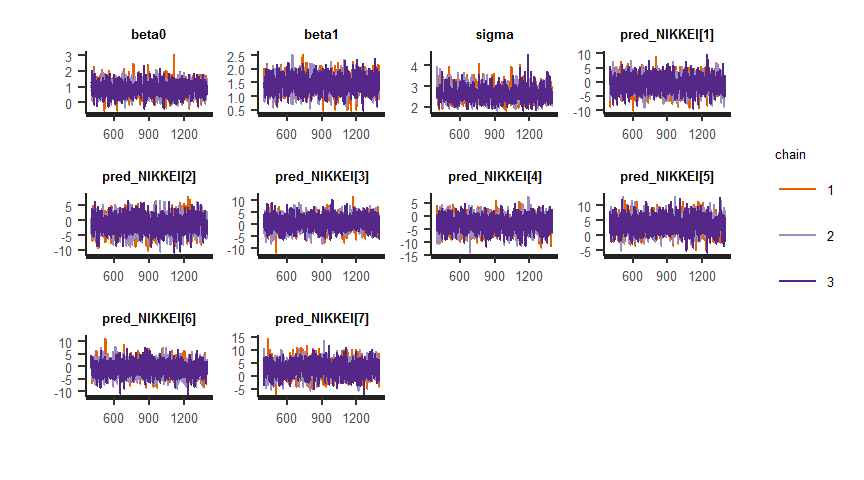
# EAP:事後期待値
df_result <- rstan::extract(fit)$pred_NIKKEI %>% data.frame() %>% gather() %>% dplyr::mutate(id = rep(c(1:N), each = (iter - warmup) * chains)) %>% group_by(id) %>% dplyr::summarize(pred_EAP = mean(value), pred_lower = quantile(value, 0.025), pred_upper = quantile(value, 0.975)) %>% dplyr::ungroup() %>% cbind(data.frame(NIKKEI, USDJPY))head(df_result) id pred_EAP pred_lower pred_upper NIKKEI USDJPY
1 1 -0.6670891 -5.887419 4.747134 0.67 -1.05
2 2 -1.3311440 -6.746644 4.062978 -0.03 -1.45
3 3 0.8456611 -4.601861 6.233359 0.79 -0.05
4 4 -2.8765245 -8.453013 2.506951 -3.12 -2.59
5 5 3.7032181 -1.472681 9.062403 5.29 1.94
6 6 -0.9205032 -6.276003 4.648296 1.62 -1.19tail(df_result) id pred_EAP pred_lower pred_upper NIKKEI USDJPY
31 31 1.049604 -4.285724 6.165953 2.53 0.15
32 32 -1.777217 -7.089221 3.549118 -4.46 -1.81
33 33 2.382464 -2.890374 7.561279 4.63 1.06
34 34 1.833427 -3.393662 7.165621 2.84 0.65
35 35 1.898318 -3.377486 7.176082 4.87 0.69
36 36 1.217293 -4.193934 6.568841 1.50 0.26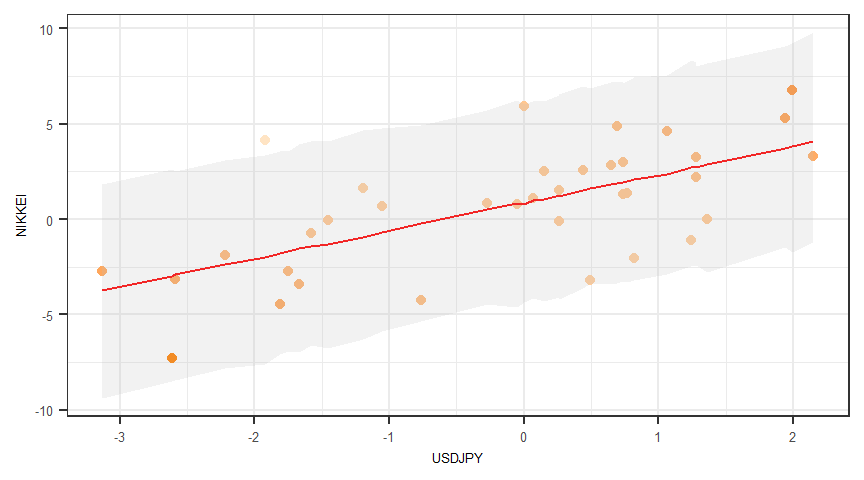
トランプ大統領の就任前後における日経平均前営業日比ボラティリティの比較
- 休日、祝日の補間はとっていない。
- helpより
- 『garchOrder The ARCH (q) and GARCH (p) orders.』
- 『external.regressors A matrix object containing the external regressors to include in the variance equation with as many rows as will be included in the data (which is passed in the fit function).』
- 参照引用Webページ
head(nikkei) Date Nikkei_ChangeRate trump
14882 2009-01-20 -2.313958 0
14883 2009-01-21 -2.035139 0
14884 2009-01-22 1.899606 0
14885 2009-01-23 -3.806506 0
14886 2009-01-26 -0.814822 0
14887 2009-01-27 4.932610 0tail(nikkei) Date Nikkei_ChangeRate trump
17554 2019-12-17 0.47498471 1
17555 2019-12-18 -0.54720080 1
17556 2019-12-19 -0.29071091 1
17557 2019-12-20 -0.20205449 1
17558 2019-12-23 0.01881039 1
17559 2019-12-24 0.03975465 1head(nikkei[as.Date("2017-1-17") <= nikkei$Date, ]) Date Nikkei_ChangeRate trump
16839 2017-01-17 -1.4752891 0
16840 2017-01-18 0.4296908 0
16841 2017-01-19 0.9414445 0
16842 2017-01-20 0.3442698 1
16843 2017-01-23 -1.2900050 1
16844 2017-01-24 -0.5454441 1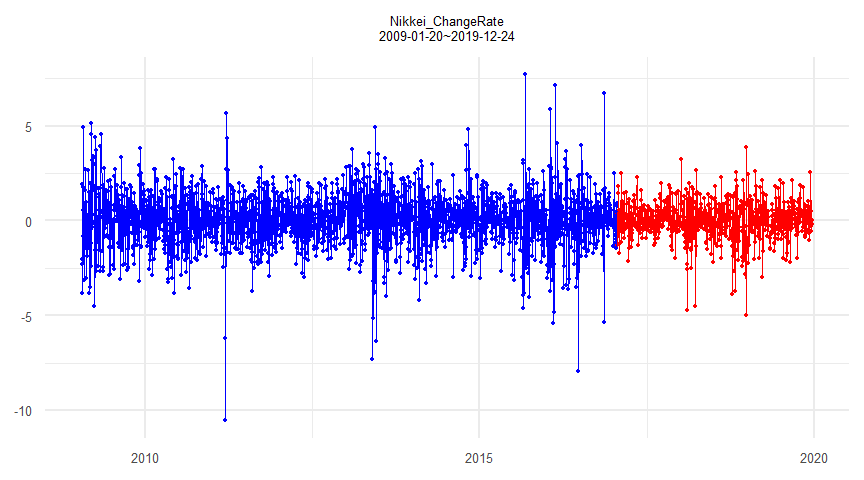
nikkei$trump <- as.numeric(nikkei$trump)datavalue <- nikkei[, 2]
trump <- as.matrix(nikkei$trump)Dummyなし
\[ r_t = \mu + \sqrt{h_t}\epsilon_t,\quad \epsilon_t\sim i.i.d. \textrm{N} (0,1),\quad h_t=\omega+\beta_{1}h_{t-1} + \alpha_{1} r^2_{t-1}\\r_tはt時点の日経平均前営業日比 \]
summary(tseries::garch(x = datavalue, order = c(1, 1)))
***** ESTIMATION WITH ANALYTICAL GRADIENT *****
I INITIAL X(I) D(I)
1 1.623355e+00 1.000e+00
2 5.000000e-02 1.000e+00
3 5.000000e-02 1.000e+00
IT NF F RELDF PRELDF RELDX STPPAR D*STEP NPRELDF
0 1 2.078e+03
1 3 2.059e+03 9.23e-03 2.35e-02 3.1e-02 4.9e+03 1.0e-01 5.73e+01
2 5 2.058e+03 5.60e-04 6.00e-04 2.4e-03 5.2e+02 1.0e-02 3.96e+00
3 7 2.056e+03 9.00e-04 9.04e-04 5.1e-03 2.0e+00 2.0e-02 1.24e+00
4 9 2.053e+03 1.25e-03 1.27e-03 1.2e-02 2.1e+00 4.0e-02 1.24e+00
5 12 2.036e+03 8.28e-03 1.40e-02 2.2e-01 2.4e+00 6.7e-01 1.33e+00
6 14 1.958e+03 3.85e-02 3.58e-02 5.0e-01 2.0e+00 6.7e-01 2.45e+00
7 16 1.952e+03 2.94e-03 9.82e-03 6.1e-02 2.2e+00 6.7e-02 2.10e-01
8 17 1.942e+03 5.21e-03 4.74e-03 6.1e-02 2.0e+00 6.7e-02 6.58e-01
9 18 1.928e+03 7.14e-03 5.82e-03 8.6e-02 2.0e+00 1.3e-01 6.73e-01
10 20 1.923e+03 2.94e-03 3.03e-03 1.7e-02 2.0e+00 2.7e-02 4.01e-01
11 21 1.918e+03 2.15e-03 2.12e-03 3.3e-02 2.0e+00 5.4e-02 2.16e-01
12 23 1.916e+03 1.49e-03 2.15e-03 2.1e-02 2.0e+00 3.2e-02 6.36e-02
13 24 1.913e+03 1.58e-03 1.97e-03 2.0e-02 2.0e+00 3.2e-02 5.18e-01
14 26 1.911e+03 6.85e-04 1.21e-03 1.1e-02 2.6e+00 1.7e-02 5.93e-02
15 27 1.909e+03 1.15e-03 1.19e-03 1.2e-02 2.0e+00 1.7e-02 3.45e-01
16 28 1.907e+03 1.24e-03 1.51e-03 2.0e-02 2.0e+00 3.5e-02 3.58e-01
17 30 1.905e+03 7.81e-04 1.57e-03 1.7e-02 2.0e+00 2.8e-02 6.00e-02
18 31 1.902e+03 1.51e-03 1.90e-03 1.5e-02 2.0e+00 2.8e-02 1.17e-01
19 33 1.901e+03 5.04e-04 8.07e-04 8.1e-03 3.9e+00 1.3e-02 3.76e-02
20 34 1.900e+03 8.22e-04 8.75e-04 7.5e-03 2.0e+00 1.3e-02 1.35e-01
21 35 1.898e+03 1.02e-03 1.21e-03 1.4e-02 2.0e+00 2.7e-02 1.16e-01
22 37 1.897e+03 5.00e-04 1.22e-03 1.2e-02 1.9e+00 2.4e-02 3.09e-02
23 38 1.894e+03 1.52e-03 1.92e-03 1.2e-02 1.8e+00 2.4e-02 1.65e-02
24 39 1.894e+03 2.03e-04 5.81e-04 1.3e-02 2.4e+00 2.4e-02 9.68e-03
25 40 1.892e+03 8.46e-04 1.33e-03 1.1e-02 1.7e+00 2.4e-02 4.22e-03
26 42 1.892e+03 1.76e-04 2.51e-04 3.8e-03 1.8e+00 8.0e-03 1.98e-03
27 43 1.892e+03 3.92e-05 7.67e-05 3.7e-03 1.3e+00 8.0e-03 2.09e-04
28 44 1.891e+03 3.35e-05 8.04e-05 3.3e-03 1.5e+00 8.0e-03 2.45e-04
29 45 1.891e+03 5.34e-06 6.67e-06 8.3e-04 0.0e+00 1.5e-03 6.67e-06
30 46 1.891e+03 7.71e-08 4.41e-08 3.9e-05 0.0e+00 7.0e-05 4.41e-08
31 47 1.891e+03 2.30e-08 1.70e-09 2.8e-05 0.0e+00 6.6e-05 1.70e-09
32 50 1.891e+03 1.06e-10 8.64e-11 3.4e-07 3.9e+00 8.0e-07 7.06e-10
33 63 1.891e+03 2.40e-16 2.90e-15 1.4e-11 6.6e+04 3.3e-11 6.21e-10
34 67 1.891e+03 -2.04e-15 2.64e-18 1.3e-14 7.3e+07 3.0e-14 6.21e-10
***** FALSE CONVERGENCE *****
FUNCTION 1.891483e+03 RELDX 1.280e-14
FUNC. EVALS 67 GRAD. EVALS 34
PRELDF 2.640e-18 NPRELDF 6.208e-10
I FINAL X(I) D(I) G(I)
1 6.669583e-02 1.000e+00 -3.293e-02
2 1.260811e-01 1.000e+00 1.181e-01
3 8.401724e-01 1.000e+00 1.113e-01
Call:
tseries::garch(x = datavalue, order = c(1, 1))
Model:
GARCH(1,1)
Residuals:
Min 1Q Median 3Q Max
-5.24492 -0.52032 0.05918 0.63678 4.16860
Coefficient(s):
Estimate Std. Error t value Pr(>|t|)
a0 0.066696 0.010176 6.554 0.0000000000559 ***
a1 0.126081 0.009789 12.880 < 0.0000000000000002 ***
b1 0.840172 0.012699 66.161 < 0.0000000000000002 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Diagnostic Tests:
Jarque Bera Test
data: Residuals
X-squared = 363.46, df = 2, p-value < 0.00000000000000022
Box-Ljung test
data: Squared.Residuals
X-squared = 2.9477, df = 1, p-value = 0.086garchresult <- fGarch::garchFit(formula = ~garch(1, 1), data = datavalue, trace = F)
summary(garchresult)
Title:
GARCH Modelling
Call:
fGarch::garchFit(formula = ~garch(1, 1), data = datavalue, trace = F)
Mean and Variance Equation:
data ~ garch(1, 1)
<environment: 0x0000000090dc12b0>
[data = datavalue]
Conditional Distribution:
norm
Coefficient(s):
mu omega alpha1 beta1
0.078505 0.067370 0.130548 0.835957
Std. Errors:
based on Hessian
Error Analysis:
Estimate Std. Error t value Pr(>|t|)
mu 0.07851 0.02130 3.685 0.000229 ***
omega 0.06737 0.01458 4.621 0.00000382 ***
alpha1 0.13055 0.01566 8.336 < 0.0000000000000002 ***
beta1 0.83596 0.01943 43.022 < 0.0000000000000002 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Log Likelihood:
-4347.433 normalized: -1.623388
Description:
Wed Dec 25 14:11:52 2019 by user: 20141203
Standardised Residuals Tests:
Statistic p-Value
Jarque-Bera Test R Chi^2 349.3298 0
Shapiro-Wilk Test R W 0.9839647 0
Ljung-Box Test R Q(10) 3.561866 0.9649559
Ljung-Box Test R Q(15) 8.267654 0.9126042
Ljung-Box Test R Q(20) 14.63216 0.7970545
Ljung-Box Test R^2 Q(10) 8.770687 0.5539958
Ljung-Box Test R^2 Q(15) 13.22446 0.5849653
Ljung-Box Test R^2 Q(20) 17.99165 0.5879581
LM Arch Test R TR^2 12.6677 0.3936489
Information Criterion Statistics:
AIC BIC SIC HQIC
3.249763 3.258565 3.249759 3.252947 garchresult@fit$par mu omega alpha1 beta1
0.07850523 0.06736971 0.13054763 0.83595724 Dummyあり
\[ r_t = \mu + \sqrt{h_t}\epsilon_t,\quad \epsilon_t\sim i.i.d. \textrm{N} (0,1),\quad h_t=\omega+\beta_{1}h_{t-1} + \alpha_{1} r^2_{t-1} + \delta_{\textrm{dummy}}\\r_tはt時点の日経平均前営業日比 \]
garch_sim <- function(data, v_model, garchorder, armaorder, external_regressors) {
garch_model <- ugarchspec(variance.model = list(model = v_model, garchOrder = garchorder, external.regressors = external_regressors), mean.model = list(armaOrder = armaorder, include.mean = T))
garch_result <- ugarchfit(spec = garch_model, data = data)
return(garch_result)
}garch_sim(data = datavalue, v_model = "sGARCH", garchorder = c(1, 1), armaorder = c(0, 0), external_regressors = trump)
*---------------------------------*
* GARCH Model Fit *
*---------------------------------*
Conditional Variance Dynamics
-----------------------------------
GARCH Model : sGARCH(1,1)
Mean Model : ARFIMA(0,0,0)
Distribution : norm
Optimal Parameters
------------------------------------
Estimate Std. Error t value Pr(>|t|)
mu 0.078496 0.021307 3.6840 0.000230
omega 0.067388 0.014914 4.5186 0.000006
alpha1 0.130437 0.017501 7.4533 0.000000
beta1 0.835981 0.020542 40.6960 0.000000
vxreg1 0.000000 0.012304 0.0000 1.000000
Robust Standard Errors:
Estimate Std. Error t value Pr(>|t|)
mu 0.078496 0.022608 3.4721 0.000516
omega 0.067388 0.024060 2.8008 0.005098
alpha1 0.130437 0.034129 3.8219 0.000132
beta1 0.835981 0.042182 19.8183 0.000000
vxreg1 0.000000 0.018174 0.0000 1.000000
LogLikelihood : -4347.443
Information Criteria
------------------------------------
Akaike 3.2505
Bayes 3.2615
Shibata 3.2505
Hannan-Quinn 3.2545
Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
statistic p-value
Lag[1] 0.1275 0.7211
Lag[2*(p+q)+(p+q)-1][2] 0.4871 0.6997
Lag[4*(p+q)+(p+q)-1][5] 0.9972 0.8603
d.o.f=0
H0 : No serial correlation
Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
statistic p-value
Lag[1] 1.785 0.1816
Lag[2*(p+q)+(p+q)-1][5] 3.761 0.2855
Lag[4*(p+q)+(p+q)-1][9] 5.435 0.3684
d.o.f=2
Weighted ARCH LM Tests
------------------------------------
Statistic Shape Scale P-Value
ARCH Lag[3] 0.2444 0.500 2.000 0.6210
ARCH Lag[5] 2.2187 1.440 1.667 0.4249
ARCH Lag[7] 3.0699 2.315 1.543 0.5005
Nyblom stability test
------------------------------------
Joint Statistic: 2.2715
Individual Statistics:
mu 0.02258
omega 0.40987
alpha1 0.31496
beta1 0.38790
vxreg1 0.51160
Asymptotic Critical Values (10% 5% 1%)
Joint Statistic: 1.28 1.47 1.88
Individual Statistic: 0.35 0.47 0.75
Sign Bias Test
------------------------------------
t-value prob sig
Sign Bias 0.7623 0.445961
Negative Sign Bias 1.9032 0.057126 *
Positive Sign Bias 2.6777 0.007458 ***
Joint Effect 15.9191 0.001178 ***
Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
group statistic p-value(g-1)
1 20 78.42 0.000000003483
2 30 97.35 0.000000002588
3 40 106.38 0.000000036719
4 50 129.39 0.000000003535
Elapsed time : 0.4200239 garch_sim(data = datavalue, v_model = "eGARCH", garchorder = c(1, 1), armaorder = c(0, 0), external_regressors = trump)
*---------------------------------*
* GARCH Model Fit *
*---------------------------------*
Conditional Variance Dynamics
-----------------------------------
GARCH Model : eGARCH(1,1)
Mean Model : ARFIMA(0,0,0)
Distribution : norm
Optimal Parameters
------------------------------------
Estimate Std. Error t value Pr(>|t|)
mu 0.039469 0.018666 2.1145 0.034472
omega 0.048555 0.008707 5.5768 0.000000
alpha1 -0.130764 0.014568 -8.9758 0.000000
beta1 0.926704 0.011290 82.0837 0.000000
gamma1 0.204104 0.021111 9.6679 0.000000
vxreg1 -0.052201 0.012956 -4.0290 0.000056
Robust Standard Errors:
Estimate Std. Error t value Pr(>|t|)
mu 0.039469 0.018293 2.1576 0.030958
omega 0.048555 0.013575 3.5768 0.000348
alpha1 -0.130764 0.031889 -4.1005 0.000041
beta1 0.926704 0.018905 49.0200 0.000000
gamma1 0.204104 0.028291 7.2145 0.000000
vxreg1 -0.052201 0.018491 -2.8230 0.004758
LogLikelihood : -4291.448
Information Criteria
------------------------------------
Akaike 3.2094
Bayes 3.2226
Shibata 3.2094
Hannan-Quinn 3.2142
Weighted Ljung-Box Test on Standardized Residuals
------------------------------------
statistic p-value
Lag[1] 0.1647 0.6849
Lag[2*(p+q)+(p+q)-1][2] 0.5559 0.6680
Lag[4*(p+q)+(p+q)-1][5] 0.8880 0.8845
d.o.f=0
H0 : No serial correlation
Weighted Ljung-Box Test on Standardized Squared Residuals
------------------------------------
statistic p-value
Lag[1] 0.0009056 0.9760
Lag[2*(p+q)+(p+q)-1][5] 0.6053180 0.9403
Lag[4*(p+q)+(p+q)-1][9] 1.6258991 0.9446
d.o.f=2
Weighted ARCH LM Tests
------------------------------------
Statistic Shape Scale P-Value
ARCH Lag[3] 0.003485 0.500 2.000 0.9529
ARCH Lag[5] 1.221804 1.440 1.667 0.6684
ARCH Lag[7] 1.421639 2.315 1.543 0.8369
Nyblom stability test
------------------------------------
Joint Statistic: 0.9803
Individual Statistics:
mu 0.08740
omega 0.07265
alpha1 0.23937
beta1 0.11870
gamma1 0.38681
vxreg1 0.01974
Asymptotic Critical Values (10% 5% 1%)
Joint Statistic: 1.49 1.68 2.12
Individual Statistic: 0.35 0.47 0.75
Sign Bias Test
------------------------------------
t-value prob sig
Sign Bias 0.7846 0.4328
Negative Sign Bias 0.3202 0.7488
Positive Sign Bias 1.6208 0.1052
Joint Effect 2.8228 0.4198
Adjusted Pearson Goodness-of-Fit Test:
------------------------------------
group statistic p-value(g-1)
1 20 56.71 0.00001266
2 30 71.38 0.00001958
3 40 77.55 0.00023487
4 50 98.18 0.00003875
Elapsed time : 0.619035
分析設計